1. Introducción
La descarga máxima en una alcantarilla circular se produce, no cuando la alcantarilla está llena,
sino cuando la alcantarilla está casi llena. La razón de este comportamiento es que a una cierta profundidad
relativa y/D (en la cual y es la profundidad de flujo y D es el diámetro de la alcantarilla), el perímetro mojado comienza
a crecer más rápidamente que el área de flujo y, en consecuencia, el caudal comienza a disminuir.
En este artículo se calcula
la profundidad relativa y/D que corresponde al caudal
máximo en una
alcantarilla circular.
2. Derivación
De acuerdo con la ecuación de Manning, el caudal es
(Ponce, 2014):
en la cual Q = caudal, A = área de flujo, R = radio hidráulico, S = pendiente de fondo, y n = coeficiente de fricción de Manning. Dado que R = A / P, el caudal es:
En términos de r y θ, el área de flujo y perímetro mojado son, respectivamente (Fig. 1):
Fig. 1 Definición de las variables.
Por lo tanto:
La profundidad relativa es (Fig. 1):
De acuerdo al
cálculo diferencial, el caudal máximo se produce cuando dQ/dθ = 0.
Utilizando la
Operando en las derivadas:
Simplificando:
Reemplazando las Ecs. 3 a 6 en la Ec. 10:
Simplificando:
Resolviendo para θ:
θ = 302° 25' 51,96".
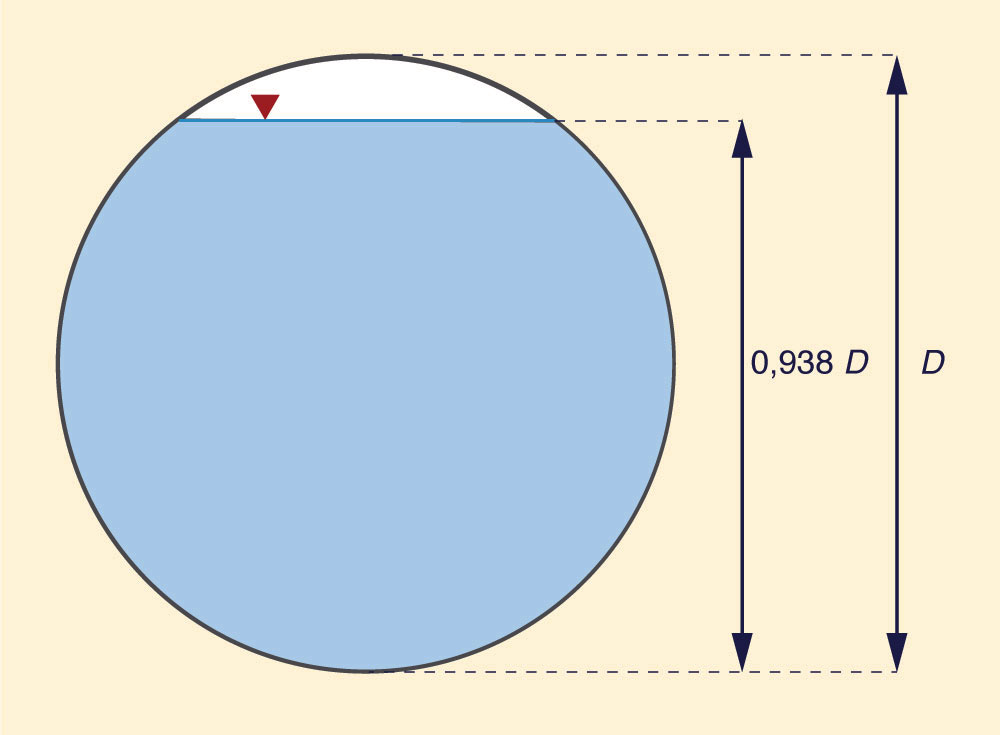
Reemplazando este ángulo en la Ec. 7, se obtiene la profundidad relativa: y/D = 0,938 (Fig. 2).
Fig. 2 Profundidad relativa correspondiente al caudal máximo en una alcantarilla circular.
3. Resumen
Se ha calculado la profundidad relativa y/D
correspondiente al caudal máximo
en una alcantarilla circular. Este valor es: y/D = 0.938.
Esto se debe a que cuando la profundidad de flujo
aumenta más allá
del valor y = 0.938D,
el perímetro mojado crece más rápidamente
que el área de flujo; por lo tanto, el caudal, dado por la Ec. 2,
disminuye.
Bibliografía
Ponce, V. M. 2014. Fundamentos de la hidráulica de canales. Texto en línea.
|
| 210118 15:55 |