Victor M. Ponce
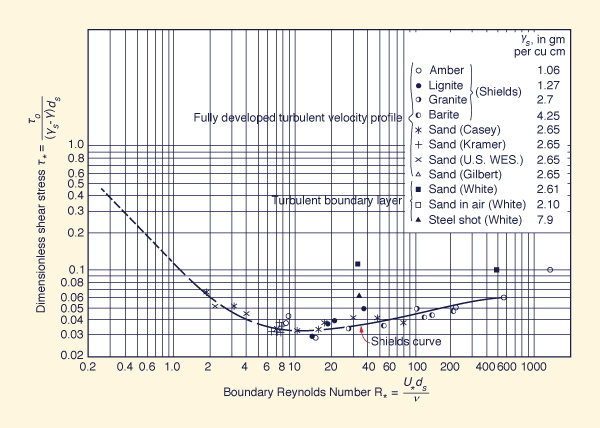
August 2011 ♦ Initiation of motion ♦ Initiation of motion is the threshold at which sediment particles start to move in open-channel flow. This threshold is important in channel design in order to assure sediment movement and avoid clogging. The Froude number F = 0.08 has often been taken as a minimum value to prevent clogging. Herein we derive a general Froude criterion for initiation of motion, confirming the validity of F = 0.08 for a wide range of practical applications. ♦ Shields criterion ♦ The Shields criterion for initiation of motion relates the dimensionless shear stress τ* with the boundary Reynolds number R*, as shown in the above figure.1 The solid curve separates motion above the curve from no motion below the curve. The Shields criterion is:
in which τo = bottom shear stress, γs = specific weight of sediment particles, γ = specific weight of water, ds = sediment particle diameter, and τ*c = dimensionless critical shear stress. For practical applications, the dimensionless critical shear stress τ*c can be taken as a constant for a wide range of boundary Reynolds numbers R*.
♦ Quadratic friction ♦ The quadratic friction formula is: 2
in which ρ = mass density of water, f = friction factor, equal to 1/8 of the Darcy-Weisbach friction factor fD, and v = mean velocity.
♦ Froude criterion ♦ The Froude number is:
in which g = gravitational acceleration and d = flow depth.
♦ Froude criterion for initiation of motion ♦ Replacing Eqs. 2 and 3 into 1:
In most cases, the ratio γs/γ = 2.65. Therefore, the Froude criterion reduces to:
As a convenient approximation, the Shields curve suggests a value of critical dimensionless shear stress τ*c = 0.04 for a wide range of boundary Reynolds numbers. Therefore:
The friction factor varies normally in the range 0.002 ≤ f ≤ 0.005, which corresponds with Darcy-Weisbach's friction factor 0.016 ≤ fD ≤ 0.040. We assume a midrange value of f = 0.0035, corresponding to fD = 0.028. The Froude criterion reduces to:
which reduces to:
For a given particle diameter, relative to the flow depth, Eq. 8 states the Froude number that must be exceeded to assure initiation of motion. For instance, for ds / d = 0.0004, i.e., a particle size of 0.4 mm in 1 m of depth, Eq. 8 reduces to:
For ds / d = 0.0003, Eq. 8 reduces to:
♦ Example ♦ Assume: (a) a friction factor f = 0.005 (a high value), and (b) a relative particle diameter ds / d = 0.0005 (a high value). The application of Eq. 6 results in:
♦ Application with Manning's n ♦ The relationship between friction factor f and Manning's n is:
in which g = gravitational acceleration, n = Manning's n, R = hydraulic radius, and k = a constant equal to 1 in SI units and 1.486 in U. S. Customary units. For a hydraulically wide channel: R ≅ d. Replacing Eq. 12 into Eq. 6, the expression for Froude number in SI units is:
For example, for d = 1 m, ds = 0.4 mm = 0.0004 m, and n = 0.020:
In U.S. Customary units, the expression for Froude number is:
in which d and ds are given in ft.
For example, for d = 1 m = 3.28 ft, ds = 0.4 mm = 0.0004 m = 0.001312 ft, and n = 0.020:
♦ Summary ♦ The Shields criterion is expressed in terms of the Froude number, enabling the calculation of the minimum Froude number for initiation of [bed material sediment] motion in open-channel flow. Given critical dimensionless shear stress, friction factor, and relative particle diameter, the developed relation confirms the validity of Froude number F = 0.08 as a convenient descriptor of initiation of motion in most cases of practical interest. 1 Ponce, V. M. 1989. Engineering Hydrology, Principles and Practices. Prentice-Hall, Englewood Cliffs, New Jersey. 2 Ponce, V. M., and D. B. Simons. 1979. Shallow wave propagation in open channel flow. ASCE Journal of the Hydraulics Division, Vol. 103, HY12, 1461-1476. |
| 200827 |