1. INTRODUCTION The Muskingum method and its variations are well established in the flood routing literature. Traditionally, its parameters K and X have been determined by calibration using measured inflow and outflow hydrographs. An improved version is due to Cunge (4), who showed that parameters K and X could be related to the physical problem, thus eliminating the need for trial and error calibration while at the same time enhancing the predictive capabilities of the method. With the aid of
Cunge's findings, the calculations can proceed either in a lumped parameter mode (5), or in a variable parameter mode (6,7).
The calculations for the lumped parameter mode can proceed in one of two ways. 2. MUSKINGUM METHOD In the Muskingum method, outflow discharge Qj+1n+1 is expressed as follows (refer to Fig. 1)
in which C1, C2 and C3 are coefficients defined as follows:
3. SIMPLIFIED MUSKINGUM ROUTING EQUATION In Eqs. 2-4, if Δt /K and X are specified as follows:
it follows that:
leading to the simplified form of the Musking routing equation as follows:
The satisfaction of Eqs. 5 and 6 implies that Δx and Δt are fixed. In effect, K is defined as the time it takes a flood discharge to travel distance Δx with celerity c:
Therefore, from Eqs. 5 and 9:
in which C = the Courant number. Equation 10 specifies that the flood wave celerity c be equal to the "grid celerity" Δx /Δt. Cunge (4) has shown that parameter X can be related to the physical problem as follows:
in which q = unit-width discharge; and So = channel bed slope. Equations 6 and 11 lead to:
in which D = grid Reynolds number. Equation 12 specifies that channel diffusivity q /(2So) be equal to "grid diffusivity" (cΔx)/2. Equations 10 and 12 enable the calculation of Δx and Δt as a function of the flow variables. In this regard, it should be noted that the space interval computed from Eq. 12 is the same as the "characteristic length" on which the Kalinin-Milyukov method is based (6). While this similarity is recognized, the method proposed herein stands on its own merits since it leads to a routing equation (Eq. 8) which is much simpler than that of the Kalinin-Milyukov method.
From Eqs. 10 and 12, the space and time intervals are given by:
and
For natural (nonprismatic) channels, the channel friction and cross-sectional shape are implicitly stated in the steady-state discharge-area relation:
in which A = cross-sectional flow area; and α and β = coefficient and exponent, respectively.
in which B = top width. From Eqs. 13 and 16:
and
As with all lumped parameter models (5), some judgement is required in the choice of the reference hydraulic variables (i.e., q, A and B in Eqs. 16-18) on which to base the calculations of Δx and Δt. The use of average quantities is usually sufficient from the standpoint of accuracy. 5. MODEL TESTING The testing of a mathematical model usually hinges upon whether the model can reproduce measured field data. When discrepancies occur, however, it is very difficult and sometimes impossible to determine whether they are due to errors in the numerical solution, in the estimation of the parameters, or in the measured data. A procedure currently open to question (2) consists of lumping all these errors into one, and adjusting the model parameters to fit the measured data in what has been referred to as "calibration". A sounder approach consists of isolating the sources of error in order to study their effects separately. This is done by performing both a hypothetical test and a real data test. The hypothetical test is designed to isolate the effects of numerical accuracy on the model results. On the other hand, the real data test is designed to provide information on the accuracy of the parameter estimation. Errors in the measured data can only be assessed from a qualitative standpoint.
Hypothetical Test. A hypothetical test using the classical example of Thomas (10) was set up to test the method proposed herein. The following two runs were made: (1) A test run using the simplified method; and (2) a control run using the conventional method. In the test run, X was made equal to zero and K equal to Δt. Accordingly, the space and time intervals were calculated to be
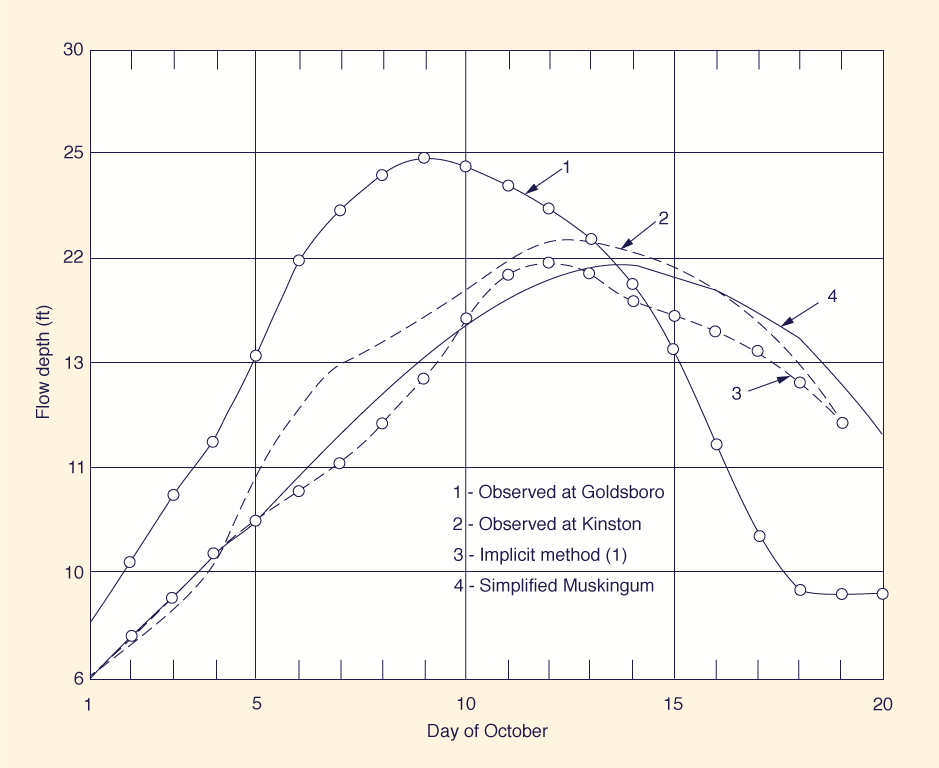
In the control run, the space and time intervals were specified to be Δx = 25 miles (40 km) and The calculated results for peak outflow = 177 cfs (5.1 m3/s), travel time = 128 hr, and hydrograph shape were essentially the same for both runs. Therefore, the demonstrated grid-independence of the results can be taken as a measure of the soundness of the simplified method. Real Data Test. A real data test using flood data measured by the United States Geological Survey in the 45-mile (72-km) reach of the Neuse River, between Goldsboro, N.C. and Kinston, N.C., was set up to further test the method proposed herein. The details of the data are given in Amein and Fang (1) and Chen (3).
The reference cross-sectional area and top width were chosen to correspond to the average hydraulic depth in the reach: A = 17,900 square ft (1,660 m2); and B = 2,900 ft (890 m). The average rating curve constants are the following: α = 12, and β = 0.74; and the channel bed slope is
at Goldsboro and Kinston, North Carolina (1 ft = 0.305 m).
The following general observations are made (Fig. 2):
6. SUMMARY AND CONCLUSIONS A simplified Muskingum routing equation is developed. The method is based on the specification of the space and time intervals Δx and Δt such that X = 0 and K = Δt. In this case, the routing equation reduces to the computation of a simple average. Testing of the method shows that reasonably accurate results can be obtained with a minimum of computational effort.
APENDIX I. DERIVATION OF LATERAL INFLOW TERM The Muskingum routing equation with lateral inflow is the following:
in which:
Since c = Δx / K, and for the condition K = Δt and X = 0, Eq. 20 reduces to:
APENDIX II. REFERENCES
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220309 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |