|
WATER BALANCE USING CATCHMENT WETTING
|
1. INTRODUCTION
The concept of catchment wetting due to L'vovich (1979) enables an improved water balance
than that which is possible using conventional methods.
Given a set of paired precipitation and streamflow data,
and using an appropriate baseflow separation technique, L'vovich's method enables
the calculation of the matrix of
precipitation-runoff-surface_runoff-baseflow-wetting-vaporization.
This provides an improved understanding of all the components of the water balance for a given gaged catchment.
2. THE WATER BALANCE
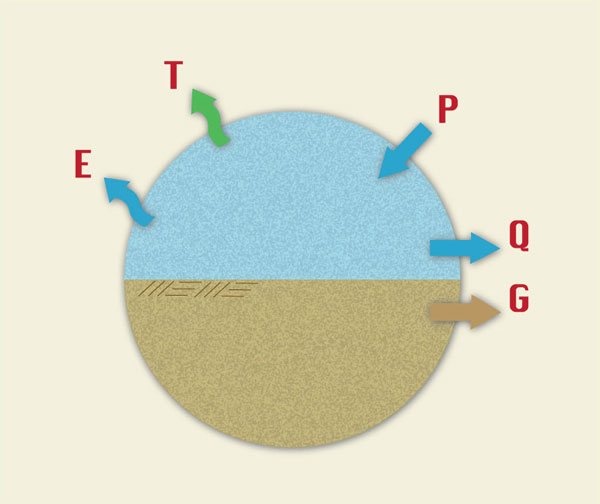
A watershed/basin water balance is the process by which precipitation is separated into its various components.
For the entire system, consisting of surface water and groundwater,
precipitation P
separates into four components (Fig. 1):
evaporation E,
evapotranspiration T,
direct surface runoff Q,
and groundwater flow G,
the majority of which eventually appears as baseflow, i.e., indirect
surface runoff.
This leads to the following water balance equation for the entire system:
| P = E + T + Q + G | (1) |
|
Fig. 1 Components of the water balance for the entire system.
Equation 1 purposefully does not include deep percolation DP, which is
the amount of groundwater flow which does not appear as baseflow G,
thereby avoiding the surface waters altogether.
According to L'vovich (1979), on a global basis, deep percolation is generally less than 1.5%
of precipitation; therefore, it may be
neglected on practical grounds.
For a surface water balance, excluding groundwater, precipitation P separates into four components (Fig. 2):
- evaporation E,
- evapotranspiration T,
- surface runoff Q, and
- infiltration I.
This leads to the following water balance equation:
| P = E + T + Q + I | (2) |

|
Fig. 2 Components of the surface-water balance.
A source of complexity in a water balance using Eq. 2 is the unknown fate of
infiltration (Ponce and Shetty, 1995). In fact, infiltration may take one of
several paths:
Return to the atmosphere as evaporation E , from lakes, ponds and swamps,
Return to the atmosphere as evapotranspiration T, through vegetation, or
Reach the groundwater table and eventually exfiltrate as baseflow to join the surface runoff Q.
Historically, this veritable double counting has defied accuracy in conventional water balance models. Depending on the prevailing climate, infiltration is split between evaporation and evapotranspiration and the fraction of Q which originates in baseflow. In arid regions, infiltration goes mostly to E and T; conversely, in humid regions, it goes mostly to baseflow, i.e., to runoff Q.
The source of the problem is Eq. 2. This equation boldly assumes that infiltration is a sink, independent of E, T and/or Q, when in fact it is not. This predicament has been resolved by L'vovich (1979), who proposed a linked set of water balance equations to replace Eq. 2.
3. EVENT VS ANNUAL WATER BALANCE
A water balance equation applicable to a storm event is the following:
| P = Q + L | (3) |
in which L = losses, or hydrologic abstractions, defined as follows:
| L = N + D + E + T + I | (4) |
in which N = interception by the vegetation canopy, D = depression storage, and all other terms have been defined previously (Ponce, 1989). Both N and D eventually convert into either E, T, or I.
In contrast to Eq. 3, a water balance equation applicable on an annual basis is:
| P = R + V | (5) |
in which R = runoff, or annual runoff yield; and V = vaporization, i.e., the sum of all evaporation, including evaporation from ground surface and water bodies, and evapotranspiration from vegetation (Lee, 1970).
4. L'VOVICH'S WATER BALANCE
According to L'vovich, annual precipitation may be separated into two components:
| P = S + W | (6) |
in which S = surface runoff, the fraction of precipitation converted into direct surface runoff, and W = watershed/basin wetting, or simply "wetting," i.e., the fraction of precipitation not converted to direct surface runoff.
Wetting may be separated into two components:
| W = U + V | (7) |
in which U = baseflow, the fraction of wetting which exfiltrates as the dry-weather flow of streams and rivers, and V = vaporization, i.e., the fraction of wetting which returns to the atmosphere as water vapor.
Vaporization may be separated into two components:
| V = E + T | (8) |
in which E = nonproductive evaporation, hereafter referred simply to as "evaporation," and T = productive evaporation, i.e., that associated with plant transpiration, hereafter "evapotranspiration."
Nonproductive evaporation E comprises evaporation from bare ground Eg and evaporation from water bodies Ew. Thus:
| E = Eg + Ew | (9) |
Combining Eqs. 5, 6 and 7:
| R = S + U | (10) |
The set of Eqs. 5-10 constitute L'vovich's water balance equations (Fig. 3).

|
Fig. 3 Elements of L'vovich's water balance.
The baseflow coefficient, i.e., the fraction of wetting showing up as baseflow, is:
| Ku = U / W = U / (U + V ) | (11) |
The runoff coefficient, i.e., the fraction of precipitation showing up as runoff, is:
| Kr = R / P = R / (R + V ) | (12) |
5. METHODOLOGY
A methodology for catchment water balance may be formulated based on L'vovich's equation set (Eqs. 5-10). The methodology may use any consistent system of units, usually either mm or inches. Given n years of precipitation-runoff data for a certain watershed/basin, the step-by-step procedure follows (SI units).
Assemble the annual precipitation data P (mm).
Assemble the corresponding annual discharge hydrographs at the mouth of the watershed/basin.
Using a suitable baseflow separation technique, separate the discharge hydrographs into a surface-runoff hydrograph S and a baseflow hydrograph U.
Integrate the surface-runoff hydrograph to obtain S (m3), and divide the latter value by the watershed/basin area A (m2), to obtain the surface runoff S (m); convert S to mm.
Integrate the baseflow hydrograph to obtain U (m3), and divide the latter value by the watershed/basin area A (m2), to obtain the baseflow U (m); convert U to mm.
With S (mm) and U (mm), use Eq. 10 to calculate runoff R (mm).
With P (mm) and S (mm), use Eq. 6 to calculate wetting W (mm).
With U (mm) and W (mm), use Eq. 7 to calculate vaporization V (mm).
With U and W, use Eq. 11 to calculate the baseflow coefficient Ku.
With P and R, use Eq. 12 to calculate the runoff coefficient Kr.
Average values of P, R, S, U, W, and V may be used as overall indicators of the watershed/basin water balance.
6. EXAMPLE
The methodology described is further explained by the example of Table 1.
Column 1 contains sequential numbers for ten (10) years of data.
Column 2 contains the precipitation record P.
Column 3 contains the runoff record R, obtained from streamgaging data.
Column 4 (S) and Col. 5 (U) are obtained from the runoff record R by using hydrograph separation techniques.
Column 6, wetting W, is calculated as: W = P - S.
Column 7, vaporization V, is calculated as: V = W - U.
Column 8, baseflow coefficient Ku, is calculated as: Ku = U / W.
Column 9, runoff coefficient Kr, is calculated as: Kr = R / P.
| Table 1. Example of L'vovich's water balance. | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| Year | P | R | S | U | W | V | Ku | Kr |
| 1 | 575 | 110 | 65 | 45 | 510 | 465 | 0.088 | 0.191 |
| 2 | 602 | 125 | 70 | 55 | 532 | 477 | 0.103 | 0.208 |
| 3 | 546 | 112 | 60 | 52 | 486 | 434 | 0.107 | 0.205 |
| 4 | 508 | 105 | 58 | 47 | 450 | 403 | 0.104 | 0.207 |
| 5 | 721 | 148 | 78 | 70 | 643 | 573 | 0.109 | 0.205 |
| 6 | 545 | 126 | 76 | 50 | 469 | 419 | 0.107 | 0.231 |
| 7 | 501 | 120 | 75 | 45 | 426 | 381 | 0.106 | 0.240 |
| 8 | 488 | 99 | 50 | 49 | 438 | 389 | 0.112 | 0.203 |
| 9 | 676 | 134 | 70 | 64 | 606 | 542 | 0.106 | 0.198 |
| 10 | 619 | 145 | 75 | 70 | 544 | 474 | 0.129 | 0.234 |
| Average | 578.1 | 122.4 | 67.7 | 54.7 | 510.4 | 455.7 | 0.107 | 0.212 |
| Note: All units are in mm, except Cols. 8 and 9, which are dimensionless. | ||||||||
The average values, shown in the last row of Table 1, confirm the accuracy and consistency of the water balance:
Eq. 5: P = R + V = 122.4 + 455.7 = 578.1 mm.
Eq. 6: P = S + W = 67.7 + 510.4 = 578.1 mm.
Eq. 7: W = U + V = 54.7 + 455.7 = 510.4 mm.
Eq. 10: R = S + U = 67.7 + 54.7 = 122.4 mm.
The online calculator onlinewaterbalance confirms the results shown in Table 1.
7. SUMMARY
The set of water balance equations developed by L'vovich are used to formulate a step-by-step procedure
to calculate annual water balance components for gaged watersheds/basins. Significantly,
L'vovich's water balance sets the method apart from conventional water balance models,
which do not consider the important element of wetting.
This results in increased accuracy and consistency in the analysis of
annual water balance.
REFERENCES
Lee, R., 1970. Theoretical estimates versus forest water yield. Water Resources Research, 6(5), 1327-1334.
L'vovich, M. I., 1979. World water resources and their future. Original in Russian. English translation,
American Geophysical Union, Washington, D.C.
Ponce, V. M., 1989. Engineering Hydrology: Principles and Practices. Pearson Education.
Ponce, V. M., and A. V. Shetty, 1995. A conceptual model of catchment water balance:
