|
FOR THREE BASINS IN CALIFORNIA San Diego State University, San Diego,
California, USA
1. INTRODUCTION
A hydrologic balance, more commonly referred to as a water balance, is a useful tool in applied hydrology. In its most basic expression, a hydrologic balance is a method of quantitatively accounting for the water entering and exiting a control volume during a given time period, while noting the transport phases of the water entering and exiting the volume. As such, all hydrologic balances must satisfy conservation of mass. In hydrology, the annual hydrologic balance of a basin is required to calculate projected flood volumes, consumptive use of irrigation, stream loads, groundwater-to-streamflow contributions, and other basin properties.
The components of the hydrologic balance equation may be assessed using physical or chemical approaches. It is common practice to separate the components of a hydrologic balance by transport phases, the latter being precipitation P, vaporization V (or E), runoff R (or Q), and ice drift in sufficiently cold climates. The transport phases may be further subdivided, typically being based on the intermediate paths of transport. Vaporization V may be subdivided into evapotranspiration T, bare-ground evaporation Eg and open-water evaporation Ew. Runoff R may be subdivided into surface flow S and baseflow U, the latter originating in groundwater G.
Two hydrologic cycle approaches are commonly used in the process of identifying hydrologic balance components: (1) cybernetic, and (2) conventional approach. The cybernetic hydrologic cycle differs from the conventional one in that it considers the interconnections and ease of transfiguration found in transport phases. The conventional hydrologic cycle prioritizes the initial transport phases. In other words, the cybernetic hydrologic cycle considers that, over a sufficient period of time, some quantities of water are likely to switch between transport phases before exiting the basin. A cybernetic hydrologic balance first considers the phase transport quantities at exfiltration and at the entrance of the basin, and then ensures that if intermediate phase transports are needed, they are mathematically consistent with the phases transports entering and exiting. A conventional hydrologic balance records the transport phases at the moment of conveyance. Because of its holistic approach, the hydrologic balance equations that rely on a cybernetic framework are believed to be more appropriate for an annual hydrologic balance (Ponce, 2018).
This paper compares two cybernetic hydrologic balances (L’vovich and Budyko) and the conventional hydrologic balance for three California basins. The three hydrologic balance equations and predicted climatic trends are discussed. Of particular interest is the difference between the precipitation predicted by the conventional method and that obtained with remotely sensed data.
Cybernetic hydrologic balances comparing the properties of different climatic types have been developed using conceptual models. Models based on measured data have been made possible by the recent availability of reliable, accessible, and precise remotely sensed data. Considerable time and attention to detail has been spent in developing cybernetic hydrologic balances using conceptual models. Thus, developing hydrologic balances with remotely sensed data may support the climate-type related predictions obtained with the conceptual models.
1.1 BASIN CHARACTERISTICS
The three basins were chosen because of their different climatic type. All the basins were fully contained within the state of California. Climatic type is defined here in terms of mean annual precipitation only. The selected basins featured a low level of development. High levels of development may cause a change in a basin’s infiltration rate, vaporization, albedo, groundwater flow, and surface runoff.
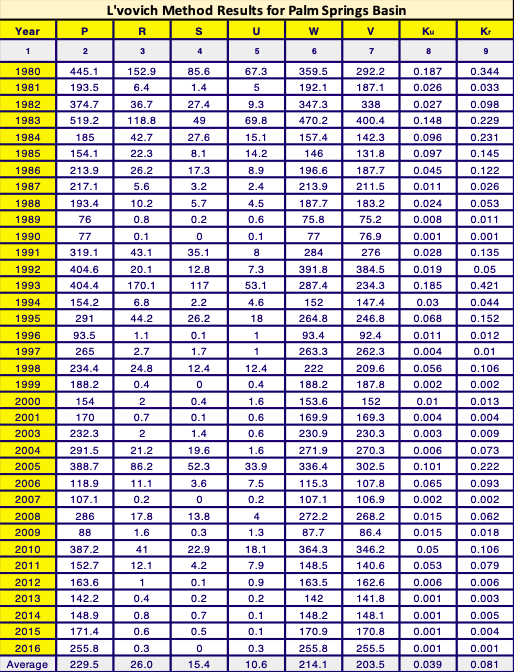
The southernmost basin is located near Palm Springs, California; hereafter, the Palm Springs basin. This basin is the smallest and the drier of the three. In the study period, the annual average precipitation was 230 mm. The area of the basin is 79.8 km2. The centroid of the basin is located at (-116.407, 33.573), at a distance of approximately 100 km from the Pacific Ocean. Its geomorphic setting is best described as mountainous, as the basin completely resides within the mountainous area of the Santa Rosa and San Jacinto Mountains National Monument. The basin has a mean elevation of 1421.9 m above sea level and an average slope of 32.4%.
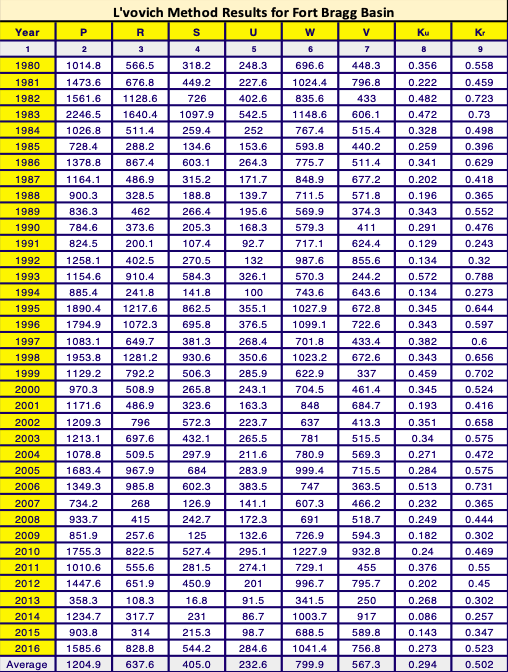
The most central of the basins is located near Fort Bragg, California. This basin is of intermediate size and climatic type. In the study period, the annual average precipitation was 1205 mm. The area of the basin is 273.3 km2. The centroid of the basin is located at (-123.573, 39.432), at a distance of approximately 23 km from the Pacific Ocean. Its geomorphic setting is best described as coastal to continental transitional. The basin has a mean elevation of 279.8 m above sea level and an average slope of 36.9%, with 71% under forest cover.
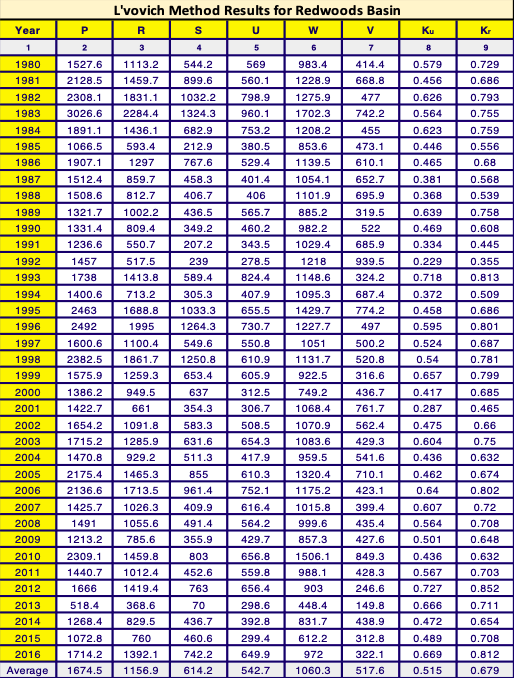
The northernmost basin is located within Redwood National Park. This basin has the largest size and the most humid climatic type. In the study period, the annual average precipitation is 1675 mm. The area of the Redwood basin is 717.6 km2. The centroid is located at (-123.889, 41.059), at a distance of approximately 21 km from the Pacific Ocean. The geomorphic setting is best described as coastal to continental transitional. The basin has a mean elevation of 558.1 m above sea level and an average slope of 32.6%, with 61.3% under forest cover. Table 1 summarizes the basin characteristics.
1.2 DATA ACQUISITION AND CHARACTERISTICS
Remotely sensed data was used to build most of the phase transport quantities for the three hydrologic balance methods used in this paper. The remotely sensed data was developed through a combination of satellite and ground-based data. All of the remotely sensed data was downloaded using NASA’s Giovanni platform. The time period was selected by choosing the longest period of overlapping datasets for each transport phase. This resulted in a temporal resolution of 37 years, from 01/01/1980 to 12/31/2016. The spatial resolution of the remotely sensed data varied between 192.5 km2 to 2. THE HYDROLOGIC CYCLE
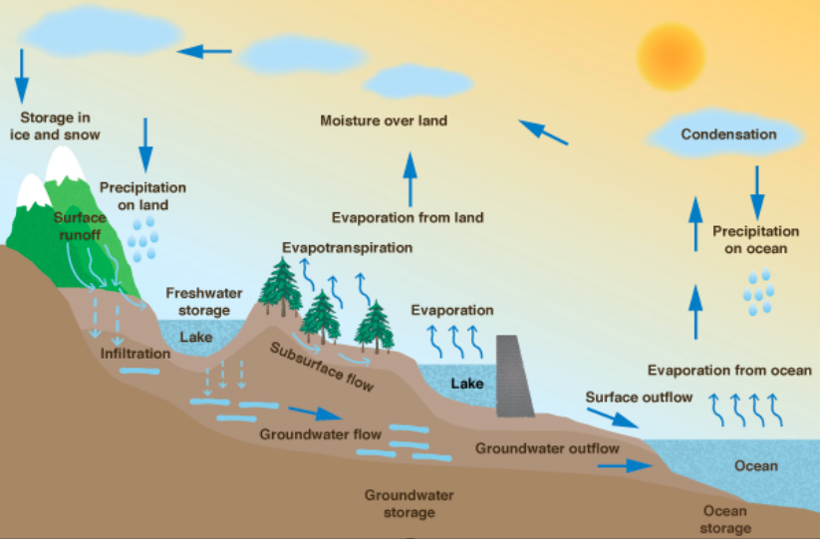
This section explains the hydrologic cycle. The aim of a hydrologic balance is to accurately capture the transport phases for a given basin over a given time. The hydrologic cycle is shown in Fig. 1. The transport phases shown are: Precipitation P, evapotranspiration T, open-water evaporation Ew, bare ground evaporation Eg, groundwater flow U, and surface flow S. Figure 1 demonstrates the ease of transfiguration of the various transport phases. Precipitation may readily become surface flow, then it may become evaporation, then precipitation once more, and may eventually exfiltrate out of the basin as groundwater flow. The recirculative closed nature of the hydrologic cycle is awknowledged. However, the inherent cybernetic properties are not apparent from
Fig. 1 The hydrologic cycle (Ponce, 2014). The hydrologic cycle by its very nature is cybernetic as are all natural systems. By creating a system of feedback mechanisms with opposing effects, natural systems can reach levels of stability high enough to promote the continuance of life. Unbalanced feedback mechanisms may also be responsible for an accelerated rate of instability that may be detrimental to life. Feedback mechanisms play an important role in hydroclimatology. An example is the role of albedo in polar ice formation. Ice formation leads to higher albedo, which leads to less emission of longwave radiation, which has the effect of reducing temperature, and thus increasing ice formation. One cybernetic feature that may be readily grasped, with the aid of Fig. 1, is the following: If precipitation falls over a forested area, the water available for evaporation will increase. Through the aid of wind, the evaporated water could make its way to an orographic barrier where (through either direct runoff, subsurface flow, or later evaporation and reprecipitation) it could make its way back to the forested area. In this manner, it could be arrgued that the trees watered themselves. Indeed, if this cycle plays an important role in the water availability of the forest, then an initial reduction in precipitation could have a further reduction in water availability later on. Thus, as an example of this principle, an initial precipitation reduction of X could produce a 1.3X total reduction of water availability. 3. CONVENTIONAL HYDROLOGIC BALANCE
3.1 BACKGROUND The conventional hydrologic balance method is that which most readers are familiar with, as follows:
In which ΔS = change in storage from year to year, P = precipitation, E = all vaporization excluding evapotranspiration, T = evapotranspiration, G = groundwater outflow, and S = surface runoff. For ΔS = 0, the following equation holds:
A hydrologic balance that accounts only for surface water is:
in which I = infiltration. Given enough time, I may transfigurate into any of the other components on the right-hand side of Eq. 3, in the following manner: I may transform into T through the local root network, I may transform into E by exfiltrating into a body of water or directly through evaporation of the topsoil, and I may transform into S by exfiltrating into a stream or river (thus forming the baseflow component). Hence, the I component may introduce double counting in Eq. 3. 3.2 CLIMATIC TRENDS AND PREDICTIONS The error induced by infiltration will grow, in any hydrologic balance based on Eq. 3, with time after the precipitation ceases. Given that a year contains numerous rainstorm events, but that a significantly larger portion of the year is taken up by the amount of time its is not raining, an annual hydrologic balance based on Eq. 3 should show a discrepancy between the left-hand and right-hand side (with the right-hand side being larger). 3.3 METHODOLOGY
The conventional hydrologic balance conducted for all three basins uses Eq. 3 as its basis. The values for P, 4. L'VOVICH'S HYDROLOGIC BALANCE
4.1 BACKGROUND L’vovich’s cybernetic hydrologic balance is defined by the following equation:
In which P = precipitation, S = surface runoff, U = baseflow, and V = vaporization. Note, that this equation does not have the issue of double counting because it avoids the use of infiltration I. Since all of the right-hand variables in Eq. 4 are measured at the point of exfiltration, it avoids the issue of considering intermediate phase transports. Notably, L’vovich also introduced the concept of catchment wetting, defined as follows:
In which W = catchment wetting value. Eq. 4 contains R = the total runoff variable, defeind as follows:
4.2 CLIMATIC TRENDS AND PREDICTIONS L’vovich’s cybernetic hydrologic balance leads to two water balance coefficients. The runoff coefficient, defined as follows:
And the baseflow coefficient defined as follows:
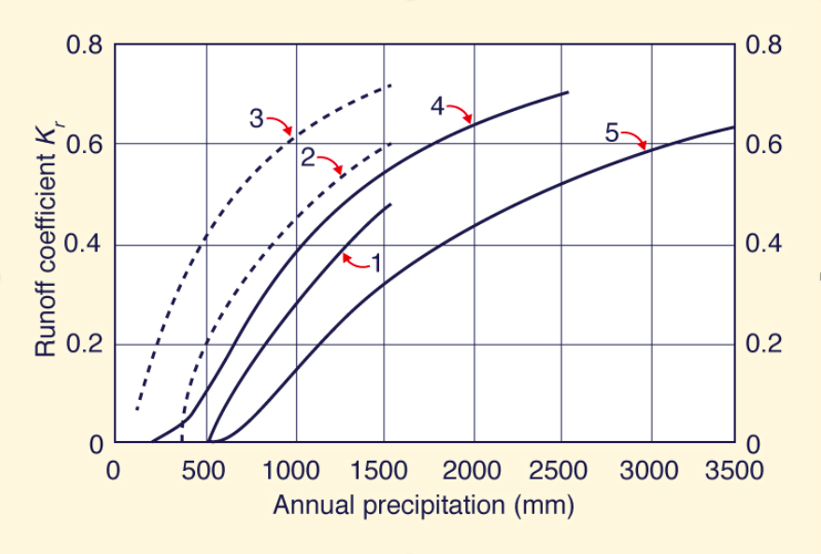
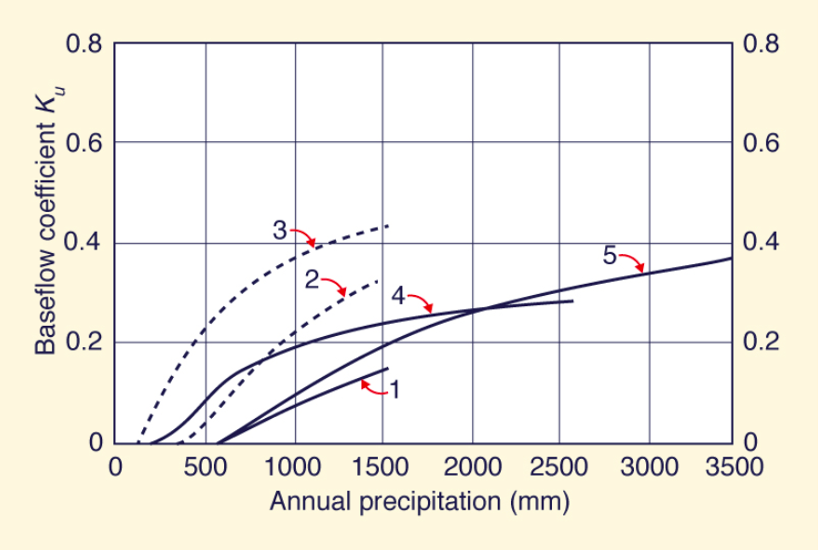
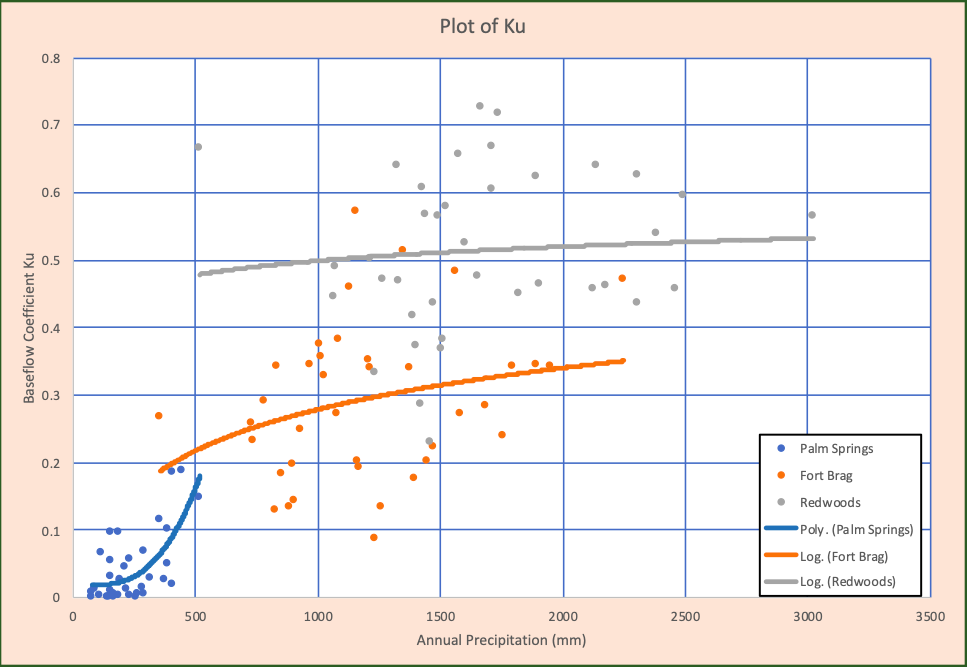
The coefficients Kr and Ku were calculated across multiple climatic types (Ponce & Shetty, 1995). The data for the Kr and Ku coefficients came from L’vovich (1979). Figure 2 and 3 show Kr and Ku distributions vs. annual precipitation across multiple climatic types (Ponce & Shetty, 1995). The climatic types are as follows:
Both water coefficients increase with increasing annual precipitation as seen in both figures (Ponce & Shetty, 1995). The same trend is expected in all basins.
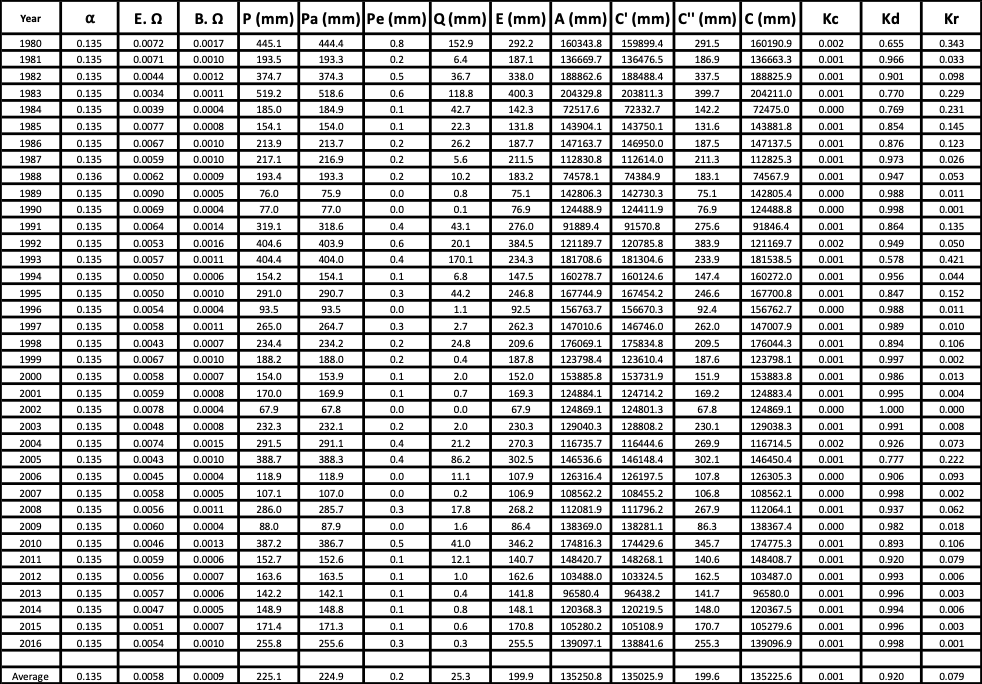
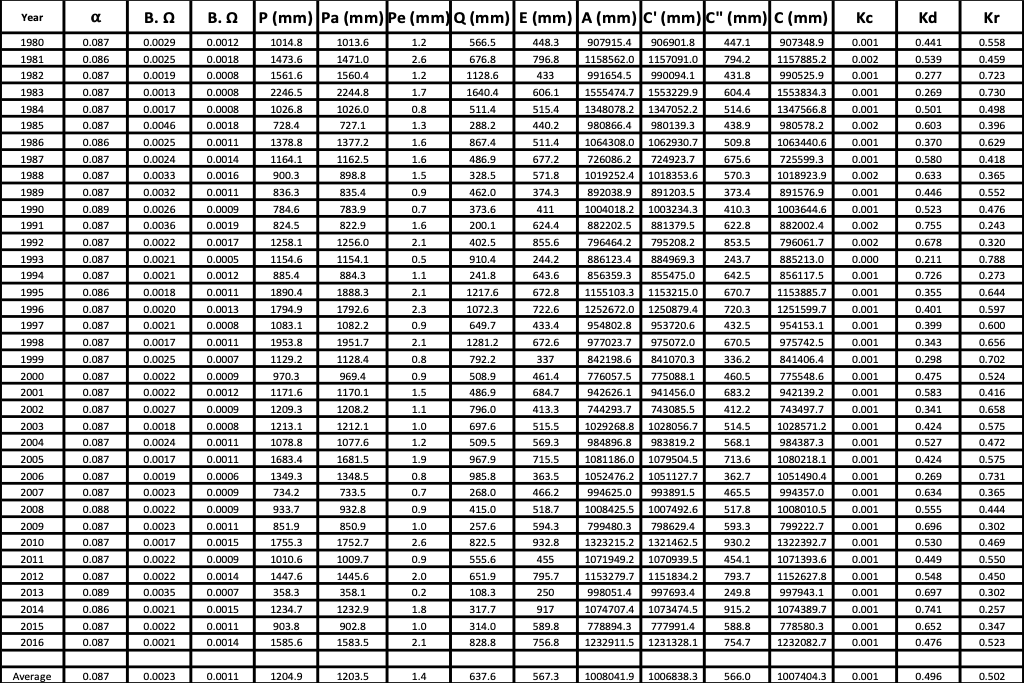
4.3 METHODOLOGY The annual hydrologic balance was developed in accordance with Eq. 4. Precipitation data was obtained through the filtration and conversion of the remote sensing product Total Precipitation Rate. Total Precipitation Rate came from the product NCALDAS Model NOAH0125_D v2.0, it had the lowest available spatial resolution of 192.5 km2 while still maintaining a daily study period. A daily study period was important in order to apply a baseflow separation technique to the streamgage data, which was also compiled in daily increments. Table 2 identifies the three USGS streamgage basins used to obtain total runoff data and their corresponding basins. Vaporization was obtained by using Eq. 4 and Eq. 6 (by subtracting R from P). Once the baseflow data was separated from the surface runoff data, the water balance coefficients were calculated.
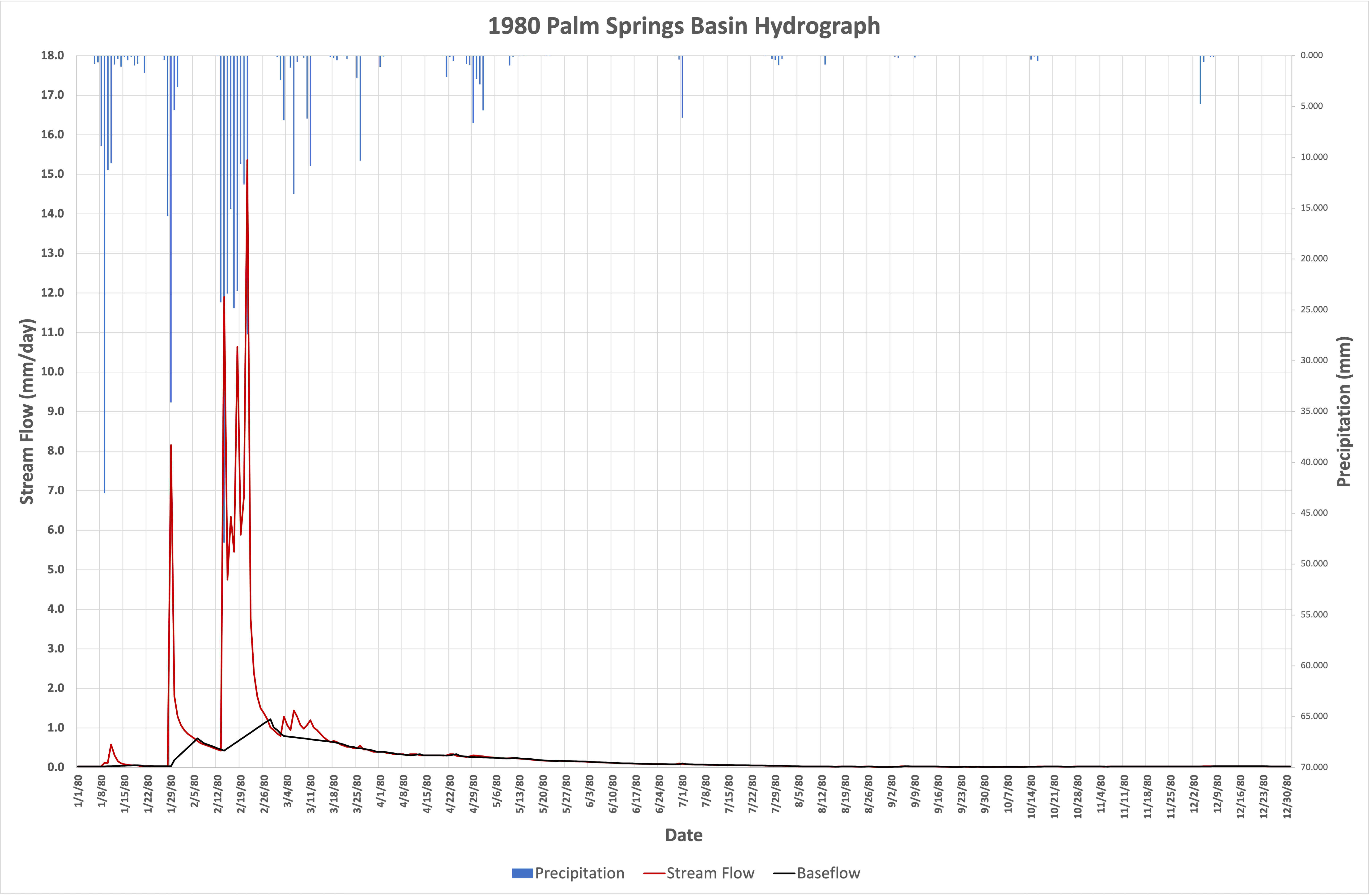
The baseflow separation technique evaluated the days of prior rainfall. If the rainfall was significantly close to zero over a certain number of days, this flow would be considered dry-weather flow (forming part of the baseflow). The dry weather data was then interpolated in-between wet weather data to create the complete baseflow data. The amount of rain considered near zero and the minimum number of days since last non-zero rainfall was adjusted by trial and error, until the baseflow was meaningful when compared to the streamgage hydrograph for each basin. Figure 4 shows the streamgage hydrograph (divided by the basin area), the baseflow, and the precipitation for the year of 1980 for the Palm Springs basin. Note that the precipitation data shows a good response to the streamgage data and that the baseflow separation technique produces a smooth baseflow response.
It should be noted, that since the precipitation data tiles had a smaller area than the basin area, the resulting precipitation was taken from the area-weighted average of the overlaying tiles. In the Redwood basin, an area of less than 3% of the total basin area was not covered by any NCALDAS tiles (located in the northeast edge of the basin). The uncovered area neighbors to the ocean, and NCALDAS does not provide coverage for oceanic data. The uncovered area was given the average data of its southernmost and easternmost neighboring tiles. As it comprised less than 3% of the basin area, this is not expected to overly hinder the results. Note that 2002 was an uncharacteristically dry year for the Palm Springs basin and only 68 mm of rainfall were recorded that year. This amount of rainfall was low enough to cause a zero-response hydrograph from the stream gage for the entire year (2002). 5. BUDYKO'S HYDROLOGIC BALANCE
5.1 BACKGROUND Budyko’s cybernetic hydrologic balance is based on the same equation as Eq. 4 repeated here in a sligthly different form:
In which P = precipitation, E = evaporation, and Q = total runoff. These are the same variables in Eq. 4, defined with different variable names in order to differentiate them. As such, Budyko’s hydrologic balance also adheres to a cybernetic structure. The differences between the hydrologic balances of Budyko and L’vovich are Budyko’s more in-depth intermediate phase transports as well as Budyko’s correlation with climatic type and albedo. Budyko’s intermediate phase transports focus on the water vapor transit and are defined in Eqs. 10-12:
In which Pa = the portion of precipitation derived from externally supplied water vapor, Pe = the portion of precipitation derived from internally supplied water vapor,
A = the horizontally advected water vapor, or the portion of the water vapor entering the basin; C = the total water vapor measured at the leeward side, or the water vapor that exfiltrates out of the basin.
C' = the portion of A that does not interact with the basin and simply leaves at the leeward side; C" = the portion of internally produced water vapor that also leaves the basin. The following equation shows how E is distributed within the intermediate phase transport quantities listed in Eqs. 10-12:
Budyko also defined a water cycle coefficient which he called K (Budyko, 1984). Budyko defined K as follows:
In which E = evapotranspiration, l = the average linear scale measurement of the basin (which is the square root of vertical projection area) (Budyko, 1984). The vertical projection of the basin can be defined by the maximum height at which water vapor is found and the average width of the basin perpendicular to the direction of the upwind. The quantity w = moisture content at the upwind boundary. Which can be calculated by identifying the specific humidity of the air column upwind. Entekhabi used symbol Ω to denote the right-most portion of Budyko’s K as follows (Entekabi et al., 1992):
The value Ω is a dimensionless climate parameter. Note, the discrepancy between Budyko’s K and Entekhabi’s Ω is not just limited to a slight difference between them. Entekhabi’s Ω uses potential evapotranspiration Ep instead of Budyko’s evapotranspiration E. Budyko’s K minus one value will henceforth be referred to as Budyko’s Ω. An important characterisitc of both Ωs is that they may be used to classify climatic properties without having to estimate other variables, like precipitation or runoff. Both Ωs should only be used to compare basins of similar sizes because of the area dependent variable l. The following Equation 16 is derived from Eq. 14:
From Budyko’s phase transport analysis, the following coefficients may be derived: (1) moisture recycling coefficient Kc, (2) water vapor discharge coefficient Kd, and (3) runoff coefficient Kr. These coefficients are useful in the classification of climatic types and are defined by the following equations:
5.2 CLIMATIC TRENDS AND PREDICTIONS Albedo is a unitless value between zero and one denoting the reflectivity of a surface to solar radiation. A value of zero denotes no reflectivity, while a value of one denotes full reflectivity. Open waters have some of the lowest albedos found in natural environments, while freshly fallen snow has some of the highest. Generally, with increasing humidity terrestrial landscapes have decreasing albedo values.
As previously discussed, albedo α is a climatic parameter that is affected by surface moisture content. A variable analysis reveals that both Ωs will be higher for larger basins. Water has a saturation limit in air; therefore, the value of w should have an upper limit as basin conditions become more humid. From a global perspective, u is highly variable and is more dependent on terrain conditions and pressure differentials than climatic type. In Budyko’s Ω, E will grow markedly as the climatic type goes from arid to humid, as water availability increases. In Entekhabi’s Ω, Ep will increase with increasing solar radiation, which is largely controlled by latitude. Given these factors, it would make sense that Budyko’s Ω would grow with increasing humidity as its numerator would grow, with its denominator eventually reaching an upper limit. Entekhabi’s Ω could grow with decreasing humidity, since the denominator decreases and the numerator grows, assuming constant or decreasing equatorial distance.
In the three basins, humidity increases as latitude increases. This means that solar radiation will decrease as humidity increases due to the increasing solar zenith angle and increasing cloud coverage. This should strengthen the relationship of increasing Entekhabi’s Ω with decreasing humidity.
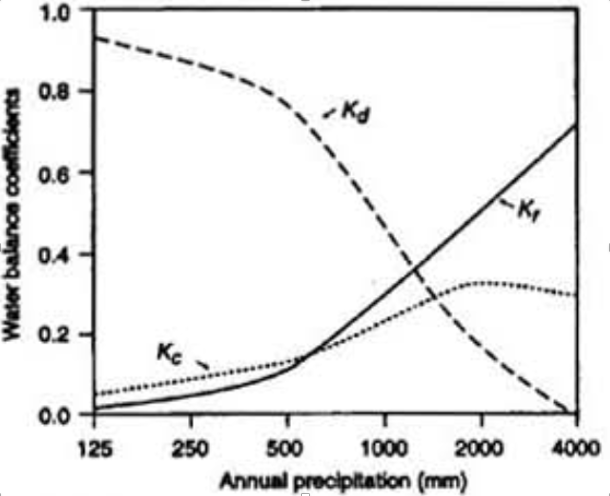
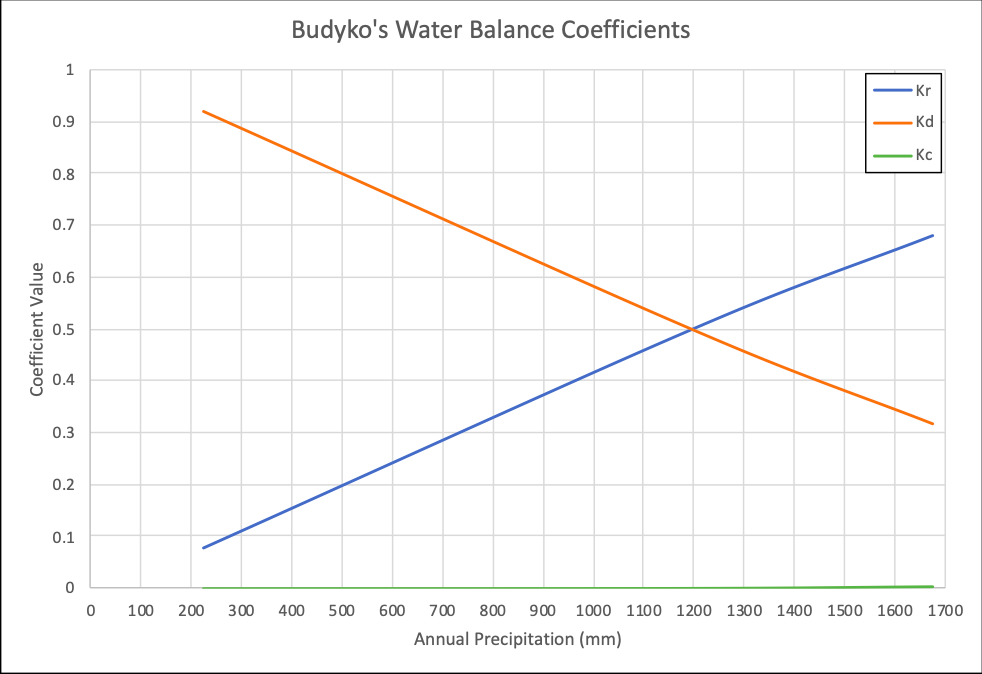
Fig. 5 Typical values of α, Budyko’s Ω, P, Pe, Pa, Q, E, A, C', C'', C, Kc, Kd, and Kr across the climatic spectrum (Ponce, 1997). Figure 5 shows that Budyko’s Ω grows with increasing humidity. However within the tropics, as distance to the equator decreases, humidity tends to increase. The hydrologic coefficients shown in Fig. 5 are visualized in Fig. 6.
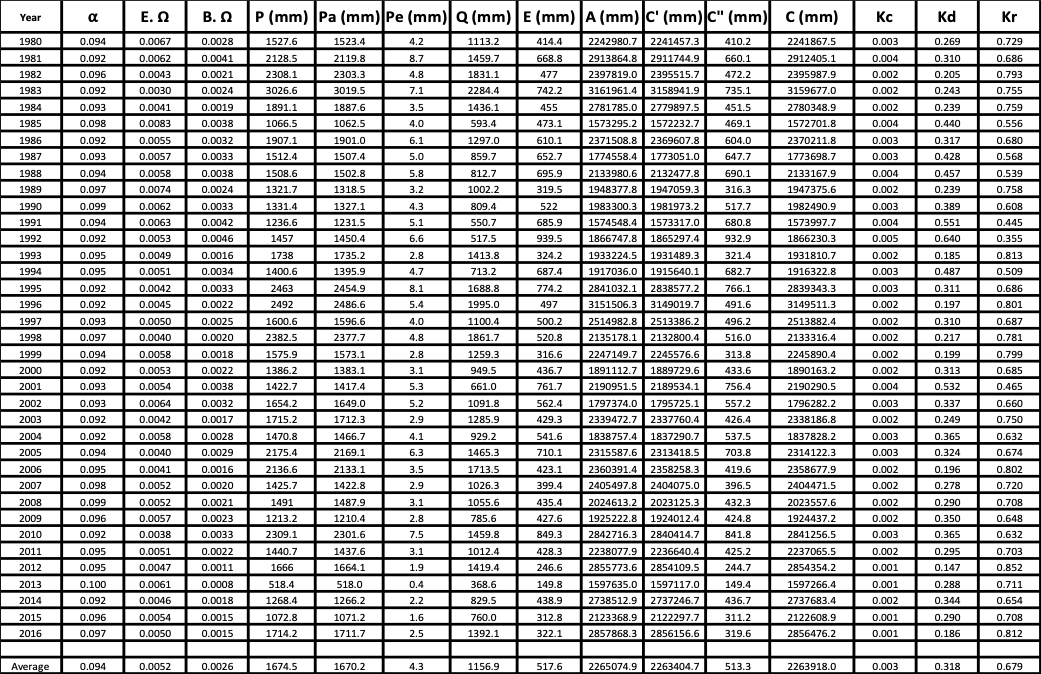
Fig. 6 Water balance coefficients (Ponce, 1997). Figure 6 shows that increasing humidity causes Kr to increase, Kd to decrease, and Kc to increase until it plateaus in the most humid climatic regions. The coefficient Kr increases with increasing humidity because the portion of water exfiltrated out of the basin by runoff grows with increasing humidity, due to saturation of both the air and ground. The coefficient Kd decreases with increasing humidity, due to the increased conversion of evaporated moisture into precipitation (caused by increasing saturation of the air). The coefficient Kc increases with increasing humidity because a greater portion of evaporated moisture is recycled (due to greater saturation of the air). Eventually, Kc plateaus in the humid climatic region because the ground becomes saturated with water. Thus, the basin fails to recycle any additional moisture and simply exfiltrates it as additional runoff. The three study basins are expected to follow the trends shown in Fig. 6. 5.3 METHODOLOGY Albedo was found using GLDAS Model NOAH_025 cells (which have a spatial resolution four times greater than NCALDAS). The first step in identifying Budyko’s phase transports was carrying over the P, Q, and E results from the L’vovich method. Secondly, Budyko’s Ω was identified in order to obtain Pa using Eq. 16. Thirdly using Eq. 10, Pe was identified. Finally using Eq. 13, C" was identified. In order to find Budyko’s Ω, w was defined by the following equation:
in which p = pressure, q = specific humidity relative to p, Ps = surface pressure, ρL = density of liquid water, and This issue was resolved by creating an average annual specific humidity and wind direction value that is representative of the average column pressure for the MERRA-tile closest to the upwind region of the basins. These pressure, annually averaged specific humidity, and wind velocity values were then divided by the MERRA-tile’s 2-m specific humidity and 10-m wind velocity data. This created a ratio that was applied to the NCALDAS product data to get pressure and annual average values with greater spatial resolution. The wind direction was assumed to be the same as the larger MERRA-tile wind direction over the encompassed basin. Because of the limited spatial resolution, the area-weighted average wind velocity over the whole basin was considered to be the same as the entering and exiting wind velocity.
The wind direction components were used to identify the average width of the basin perpendicular to wind direction. For Budyko’s Ω, the E values obtained from L’vovich were used. For Entekhabi’s Ω, the Ep were obtained from the NCALDAS Model NOAH0125_D product. Once Budyko’s Ω was found, the three water balance coefficients were determined. In order to find the remaining A and C variables, A was found by using the annual average atmospheric water vapor flux AQg value of the upwind MERRA-tile; then Eq. 11 was used to find C. The composition of AQg value is described by the following equation:
The AQg is then multiplied by the average width of the basin, perpendicular to the wind direction, and the number of seconds in a year. The resulting value is then divided by the density of water and the area of the basin to obtain the resulting value of A applicable over the basin. 6. RESULTS OF HYDROLOGIC BALANCES
6.1 CONVENTIONAL HYDROLOGIC BALANCE RESULTS
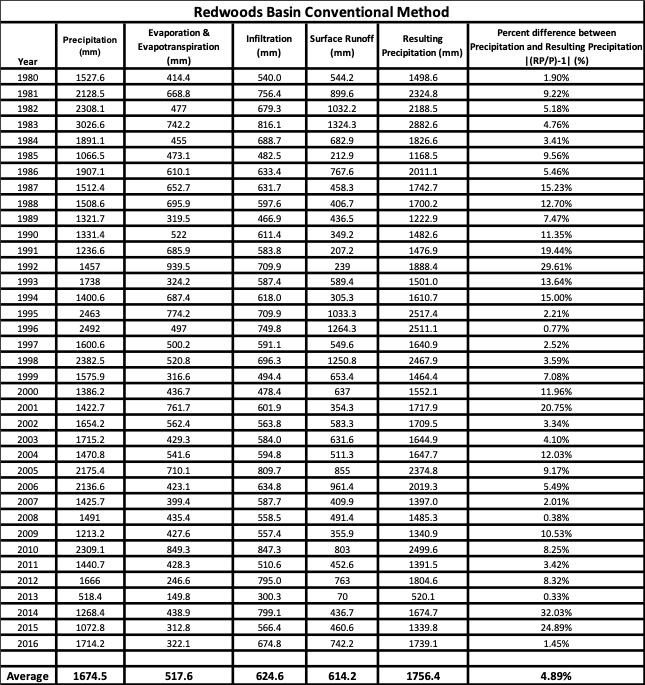
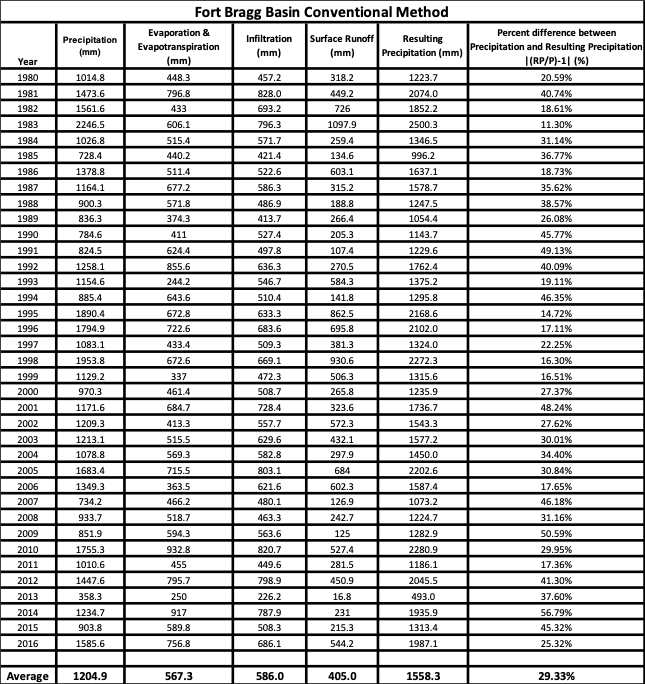
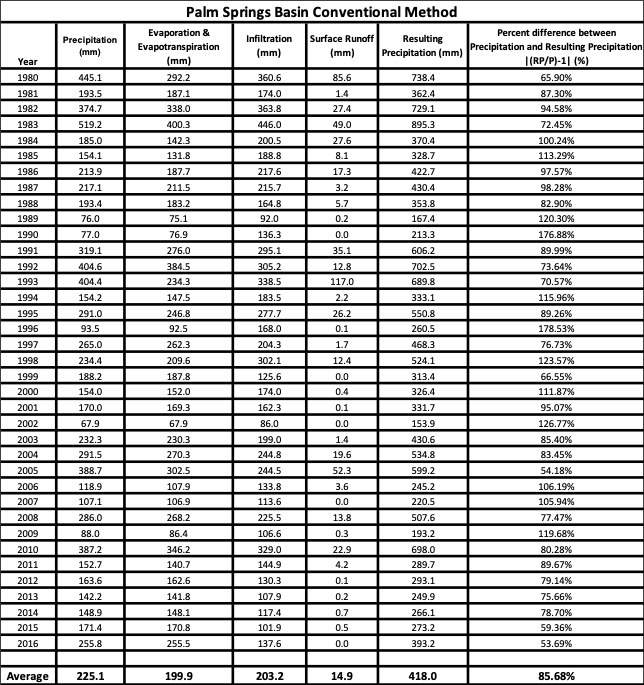
Figures 7 to 9 show the conventional results, ranging from least humid to most humid basin. Note that the percent difference between the measured and calculated precipitation increases with increasing aridity. Measured precipitation was obtained from remotely sensed data; calculated precipitation was obtained using
6.2 L’VOVICH'S CYBERNETIC HYDROLOGIC BALANCE RESULTS
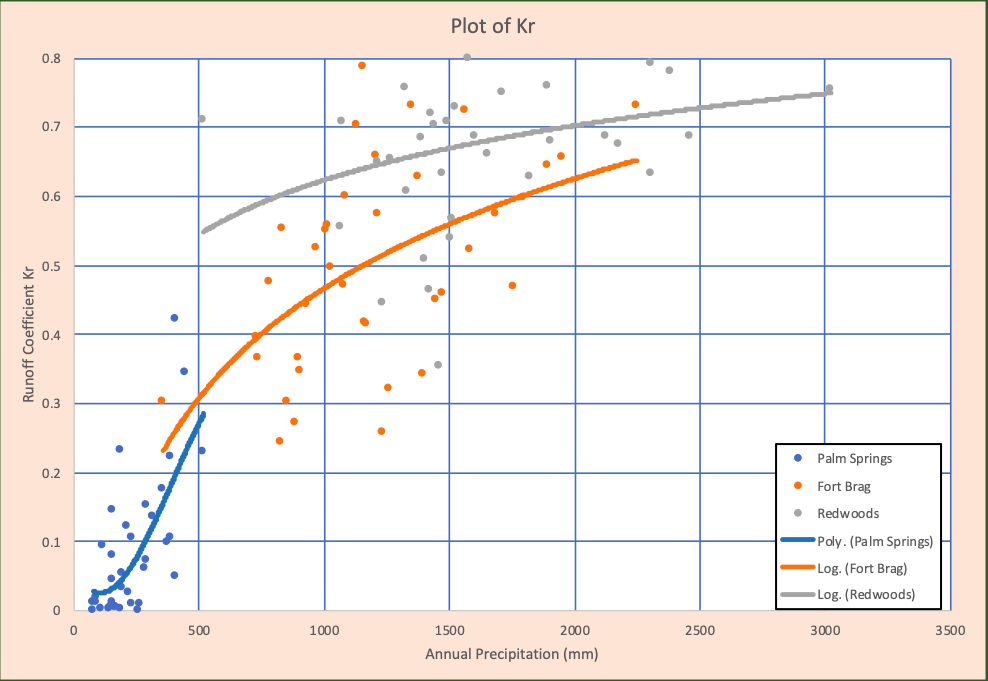
Figures 10 to 14 show the L’vovich method results, ranging from least humid to most humid basin. Note that larger slopes of Fig. 13 vs. Fig. 14. Note, the differences in trendline shape between the Palm Springs basin and the other basins in figures 13-14.
6.3 BUDYKO'S CYBERNETIC HYDROLOGIC BALANCE RESULTS
Figures 15 to 19 show the Budyko method results, ranging from least humid to most humid basin. Note the large A values and low Ω values found in figures 15-17. Also note that in Fig. 18 Entekhabi’s Ω, with constant length scale, increases with decreasing moisture. In Fig. 18, among the three basins Budyko’s Ω peaks at the Fort Bragg basin. Figure 19 shows that Budyko’s water balance coefficients follow the anticipated trends, discussed in the previous section for Kr and Kd.
7. ANALYSIS
7.1 CONVENTIONAL HYDROLOGIC BALANCE ANALYSIS
The results of Figures 7-9 show that double counting of infiltration indeed does occur. This is supported by the larger calculated precipitation than measured precipitation, a feature not found in the other hydrologic balance methods. Interestingly, the more arid the basin, the higher the discrepancy between resulting and measured precipitation. This is due to the fact that even though Eq. 3 is said to only consider surface waters, in reality infiltration will appear at the boundaries of the basin either as baseflow or vaporization. Since vaporization has already been accounted for, the more infiltration becomes baseflow, the less it is double counted. It follows that in the Palm Spring basin, where a larger amount of infiltration will exfiltrate through vaporization due to higher solar radiation and less saturated air conditions, the double counting will be greater.
7.2 L'VOVICH'S CYBERNETIC HYDROLOGIC BALANCE ANALYSIS
Figures 2-3 and 13-14 correlate nicely. Both Kr and Ku increase with increasing precipitation. This is due to the saturation limits of both the ground and air. All four figures demonstrate that the Kr slopes tend to be steeper than the Ku slopes. The difference in steepness between the two coefficients could be due to the temporal distribution of rainfall. When precipitation tends to occur in short, concentrated burst (storms), not in a temporally well distributed manner, this relationship becomes stronger as the climate becomes more arid. During concentrated periods of rainfall, the ground is likely to reach saturation quickly, resulting in a larger portion of precipitation exfiltrating as surface runoff. Figure 13 supports this theory, as the more arid a basin, the steeper its Kr slope becomes. It should be noted that while this could serve as an explanation of the differences in Kr slope, humid basins are more likely to have already saturated ground before the start of a precipitation event. However, arid regions are also likely to have more crusting form on the soil surface due to less flushing of fine particles, thus encouraging more surface runoff.
7.3 BUDYKO'S CYBERNETIC HYDROLOGIC BALANCE ANALYSIS
The most notable results come from the analysis of Budyko’s transport phases. Figures 15-17 show that Entekhabi’s Ω and Budyko’s Ω are two orders of magnitude lower than expected based on Fig. 5. This is due to the length scale component of both Ωs. Both Ωs were developed to estimate climatic properties at the regional scale, while this study was performed at a smaller scale. This points to the need for the development of a climatic type parameter that can accomplish the role of Budyko’s Ω, either at smaller lengthscales or independent of lengthscale.
Figure 18 shows both Ω values calculated with a constant 500 km length scale, which is closer to a regional scale measurement. Figure 18 reveals that Entekhabi’s Ω does indeed grow with decreasing humidity. Figure 18 also shows that the point at which Budyko’s Ω is balanced by increasing water availability and decreasing solar radiation (along California’s precipitation over latitude gradient) is somewhere near the annual precipitation and latitude value of Fort Bragg, as this represents the peak value of Budyko’s Ω.
Figure 19 confirms the expected Kr and Kd trends. It should be noted that although not in the expected order of magnitude, Kc does follow the expected trend (increasing with annual precipitation). The values of A are at least two orders of magnitude larger than those shown in Fig. 5. This is due to the basins being smaller than regional size, as well as their proximity to the Pacific Ocean, which has higher than terrestrial values of w and u. As a result of an uncharacteristically large A, the C value, was also large in accordance with Eq. 11. Albedo increased with increasing Entekhabi’s Ω. A simple inversely or conversely growing trend between Budyko’s Ω and albedo is expected in basins that don’t have opposing water availability and solar radiation trends.
8. SUMMARY AND CONCLUSIONS
The issue of double counting in the conventional hydrologic balance was confirmed and found to be greater in arid basins. This is atributed to a larger value of the vaporization to total exfiltration ratio.
The predicted global trends identified with conceptual models held for the three study basins, despite not being regionally scaled. Both the L’vovich and Budyko trends for the water balance coefficients held with measured data. This means that the conceptual models are consistent with the governing natural systems. However, this study also exemplified the need to examine relevant climatological trends. Contrary to tropical trends, in this study, basin water availability increases with decreasing solar radiation. The previous statement is consistant with the Hadley Cell, as the basins fall within 30° and 60° latitude. Barring this analysis, the results of Budyko’s Ω, with a constant 500 km lengthscale (Fig. 18), would seem incorrect in their trends.
The need for a climatic parameter that can be used in a manner similar to Budyko’s Ω, but independent of basin size, was shown to be necessary.
REFERENCES
Budyko, M. I. 1984. The evolution of the biosphere. D. Reidel Publishing Co., Boston.
Entekhabi, D., I. Rodriguez-lturbe, and R. L. Bras. 1992. “Variability in large-scale water balance with land surface-atmosphere interaction.” J. Climate, 5, 798-813.
L'vovich, M. I, 1979. World water resources and their future. Original in Russian. English translation, American Geophysical Union, Washington, DC.
Ponce, V. M., and A.V. Shetty. 1995. “A Conceptual Model of Catchment Water Balance: 2. Application to Runoff and Baseflow Modeling.” Journal of Hydrology, vol. 173, no. 1-4, 41–50., doi:10.1016/0022-1694(95)02745-b.
Ponce, V. M., A. K. Lohani, and P. T. Huston. 1997. “Surface Albedo and Water Resources: Hydroclimatological Impact of Human Activities.” Journal of Hydrologic Engineering, vol. 2, no. 4, 197–203., doi:10.1061/(asce)1084-0699(1997)2:4(197).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 210727 11:45 |