1.  INTRODUCTION

The companion paper (Ponce and Shetty, 1995) has described a conceptual model of water balance which separates annual precipitation into surface runoff and wetting, and wetting into baseflow and vaporization, following concepts suggested by L'vovich (1979). The objective is to determine the fraction of annual precipitation which goes into surface runoff and the fraction of wetting which goes into baseflow. Runoff, or streamflow, consists of surface runoff and baseflow. A competition exists between surface runoff and wetting. Any drop of water that goes into surface runoff is a drop that does not add to catchment wetting. Similarly, a competition exists between baseflow and vaporization. Any drop of water that goes into baseflow is a drop that does not leave the catchment through vaporization.

Conflicting evidence regarding this dual competition is scattered throughout the literature. On a global basis, differences in biogeographical regions and climatic settings have tended to mask the nature of the competition. For instance, Pitman (1978) has documented declining streamflow following large-scale afforestation in South Africa. Baker (1986) has reported temporary increases in streamflow following herbicide treatment in a pinyon-juniper watershed in north-central Arizona. Ruprecht and Schofield (1989) have documented increases in both surface runoff and baseflow following replacement of deep-rooted native forest species with shallow-rooted agricultural species in Western Australia. However, Ruprecht and Stoneman (1993) have stated that the long-term prognosis for annual water yield from areas subjected to forest harvesting in Western Australia is uncertain. Hibbert (1967) qualified his review of catchment experiments to increase water yield by stating that catchment response to treatment was highly variable, and for the most part, unpredictable. Nevertheless, Bosch and Hewlett (1982), in their comprehensive review of catchment experiments to increase water yield, were not inclined to support Hibbert's doubts. The issue of the competition between runoff (including baseflow) and vaporization is one of significant practical interest, as decreasing runoff is invariably associated with decreasing water resources.

In this paper we simulate runoff and baseflow using a conceptual model of water balance described in the companion paper (Ponce and Shetty, 1995). The conceptual basis of the model enhances its applicability to a wide range of biogeographical regions and climatic settings. In this paper, selected catchment data for Africa, North America, and South America (L'vovich, 1979) are supplemented with the writers' own Asian data. Two runoff and baseflow functions are derived: (1) runoff and baseflow coefficients vs annual precipitation; (2) runoff and baseflow gains vs annual precipitation. Analysis of these functions leads to a characterization of runoff and baseflow throughout the climatic spectrum, shedding additional light on the competition between runoff and vaporization, and baseflow and vaporization.

2.  THE CONCEPTUAL MODEL

Annual precipitation P can be separated into two components (Ponce and Shetty, 1995):

P = S + W

(1)

in which S is surface runoff and W is wetting. In turn, wetting is separated into two components:

W = U + V

(2)

in which U is baseflow, and V is vaporization. As used here, the term "vaporization" encompasses all moisture returned to the atmosphere by evaporation: evapotranspiration from vegetated areas, evaporation from nonvegetated areas, and evaporation from water bodies.

Runoff consists of surface runoff and baseflow:

R = S + U

(3)

Combining Eqs. (1)-(3) yields

P = R + V

(4)

The runoff coefficient is:

R Kr = ____         P

(5)

The vaporization coefficient is:

V Kv = ____ = 1 - Kr           P

(6)

Runoff gain is defined herein as:

dKr K'r = ______           dP

(7)

Vaporization loss is the derivate of the vaporization coefficient, or also:

K'v = - K'r

(8)

The baseflow coefficient is (L' vovich, 1979):

U Ku = ____          W

(9)

Baseflow gain is defined herein as:

dKu K'u = _____            dP

(10)

The sequential separation of annual precipitation into surface runoff and wetting, and wetting into baseflow and vaporization, is modeled by a proportional relation such that wetting asymptotically reaches an upper bound as precipitation and surface runoff increase unbounded. Likewise, vaporization asymptotically reaches an upper bound as wetting and baseflow increase unbounded. The surface runoff and baseflow submodels are given as Eqs. (16) and (18) of the companion paper (Ponce and Shetty, 1995), respectively.

Given a set of model parameters λ_s, W_p, λ_u and V_p, the conceptual model separates annual precipitation into surface runoff and wetting, and wetting into baseflow and vaporization. The procedure can be applied to a realistic range of annual precipitation, from which runoff and baseflow functions (Eqs. (5), (7), (9), and (10)) are derived.

3.  MODEL APPLICATION

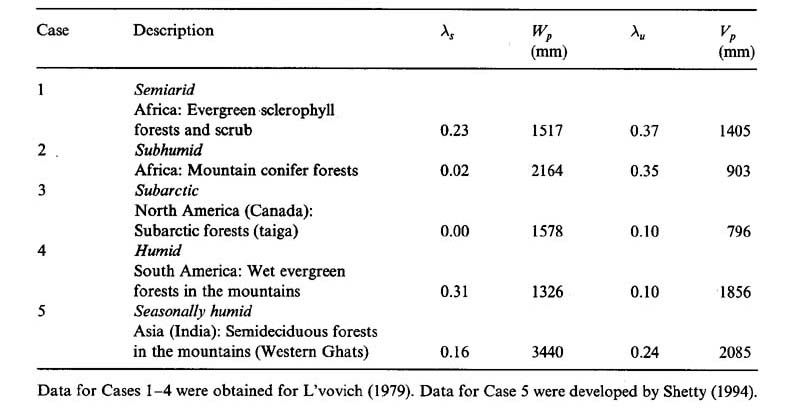
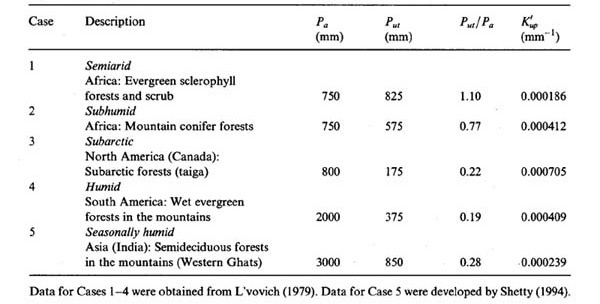
Table 1 shows calibrated model parameters for five cases. The first four cases were included in the companion paper Ponce and Shetty, 1995). In this contribution, we add a fifth case: the Malaprabha river basin at Khanapur, Karnataka (India), which consists largely of semideciduous forests in the eastern slopes of the Westem Ghats (Shetty, 1994). The Malaprabha basin has a seasonally humid climate, characterized by monsoon-driven rainfall lasting 4-5 months. The five selected cases encompass a wide range of climatic settings, as follows: Case 1: Semiarid; Case 2: Subhumid; Case 3: Subarctic; Case 4: Humid; Case 5: Seasonally humid.

Table 1.  Conceptual model parameters for selected cases.

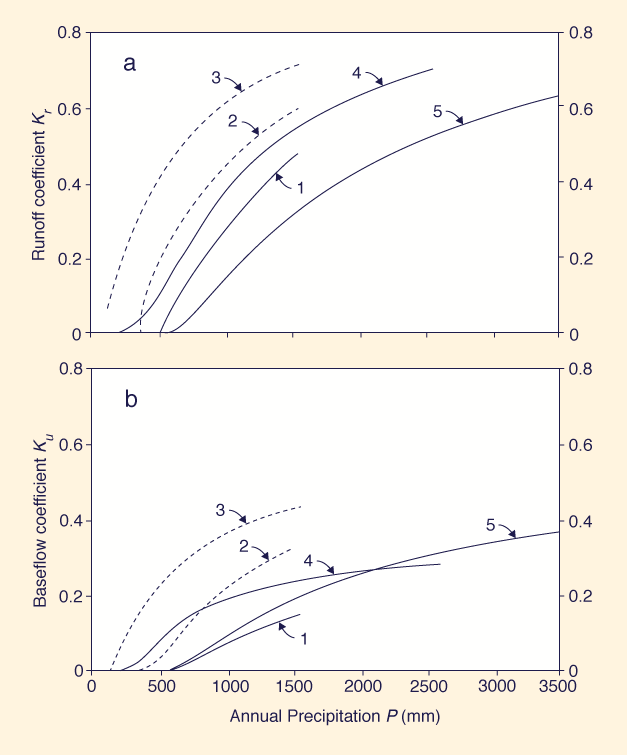
Figure 1 shows runoff and baseflow coefficients for the five cases included in this study. Analysis of this figure leads to the following conclusions:

1. Runoff and baseflow coefficients increase monotonically with annual precipitation, starting from zero in most cases. The drier the climate and the lower the annual precipitation, the more the likelihood that the coefficients will start from zero.

2. Runoff and baseflow coefficients increase markedly for low and midrange values of annual precipitation.

3. Runoff and baseflow coefficients have a tendency to reach an upper bound for high and very high values of annual precipitation.

Fig. 1. Runoff and baseflow coefficients for the five cases included in this study.

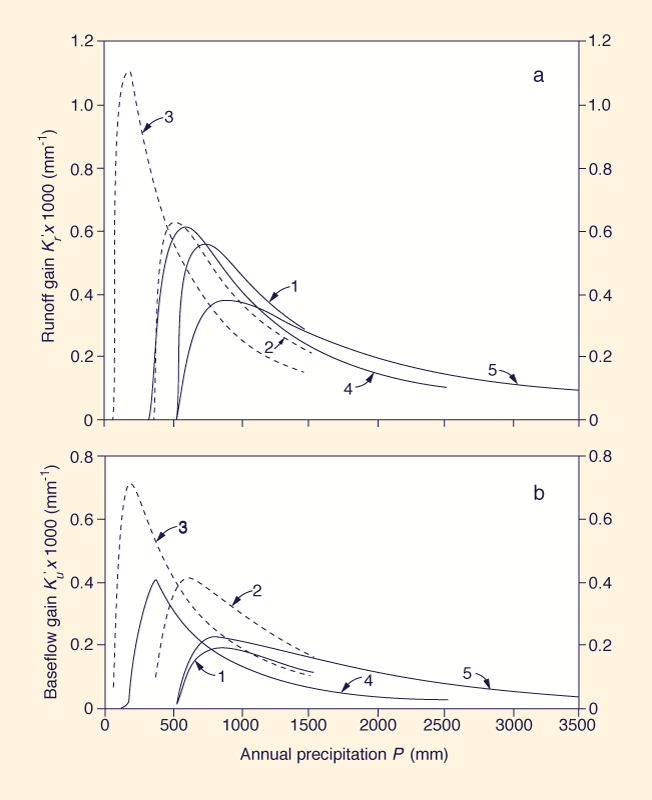
Figure 2 shows runoff and baseflow gains for the five cases included in this study. Analysis of this figure leads to the following conclusions:

1. Runoff gains are always positive, reaching a peak K'_rp at a runoff threshold precipitation P_rt.

2. Baseflow gains are always positive, reaching a peak K'_up at a basefiow threshold precipitation P_ut.

3. An increase/decrease in runoff or baseflow gain corresponds to a decrease/increase in vaporization gain, i.e. an increase/decrease in vaporization loss.

Fig. 2.  Runoff and baseflow gains for the five cases included in this study.

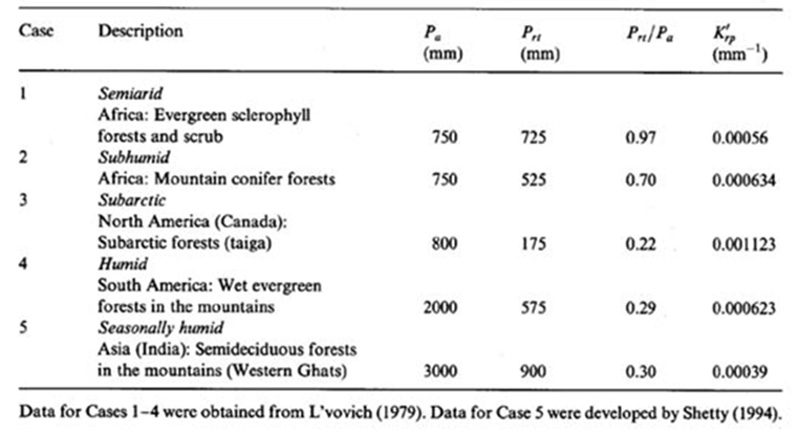
Table 2 shows mean annual precipitation, runoff threshold precipitation, ratio of runoff threshold precipitation to mean annual precipitation, and peak runoff gain for the five cases included in this study. Analysis of this table leads to the following conclusions:

1. Runoff threshold precipitation varies with the climatic setting, as follows; (a) in semiarid and seasonally humid regions, P_rt is high (725-900 mm); (b) in subhumid and humid regions, P_rt has midrange values (525-575 mm); (c) in subarctic regions, P_rt is low (175 mm).

2. Peak runoff gain varies with the climatic setting, as follows: (a) in seasonally humid regions, K'_rp is low (0.00039 mm^-1); (b) In semiarid, subhumid and humid regions, K'_rp has midrange values (0.00056-0.000634 mm^-1); (c) in subarctic regions, K'_rp is high (0.001123 mm^-1).

3. The ratio of runoff threshold precipitation to mean annual precipitation characterizes the climatic setting, as follows: (a) in semiarid regions, the value P_rt ∕P_a, is high, close to unity; for instance, the value for evergeen sclerophyll forests and scrub in Africa is 0.97; (b) in subhumid regions,P_rt ∕P_a has midrange values, less than unity; the value for mountain conifer forests in Africa is 0.70; (c) in seasonally humid, humid, and subarctic regions,P_rt ∕P_a has low values, typically less than or equal to 0.3; the measured values for Asia, South America, and North America range between 0.22 and 0.30.

Table 2.  Mean annual precipitation Pa, runoff threshold precipitation Prt, ratio Prt ∕ Pa and peak runoff gain K'rp for selected cases.

Table 3 shows mean annual precipitation, baseflow threshold precipitation, ratio of baseflow threshold precipitation to mean annual precipitation, and peak baseflow gain for the five cases included in this study. Analysis of this table leads to the following conclusions:

1. Baseflow thereshold precipitation varies with the climatic setting, as follows: (a) in semiarid and seasonally humid regions, P_ut is high (825-850 mm); (b) in subhumid and humid regions, P_ut has midrange values (370-575 mm); (c) in subartic regions,P_ut is low (175 mm).

2. Peak baseflow gain varies with the climatic setting, as follows: (a) in semiarid and seasonally humid regions, K'_up is low (0.000186-0.000239 mm^-1); (b) in subhumid and humid regions, K'_up has midrange values (0.000409 - 0.000412 mm^-1); (c) in subartic regions, K'_up is high (0.000705 mm^-1).

3. The ratio of baseflow threshold precipitation to mean annual precipitation characterizes the climate setting, as follows: (a) in semiarid regions, the value P_ut ∕P_a is high, close to unity; for instance, the value for evergreen sclerophyll forests and scrub in Africa is 1.10; (b) in subhumid regions, P_ut ∕P_a has midrange values, less than unity; the value for mountain conifer forests in Africa is 0.77; (c) in seasonally humid, humid, and subarctic regions, P_ut ∕P_a has low values typically less than 0.3; the measured values for Asia, South America, and North America range between 0.19 and 0.28.

Table 3. Mean annual precipitation Pa, baseflow threshold precipitation Put, ratio Put /Pa and peak baseflow gain K'up for selected cases.

4.  COMPETITION BETWEEN RUNOFF AND VAPORIZATION, AND BASEFLOW AND VAPORIZATION

Analysis of the runoff gain function serves to clarify the nature of the competition between runoff and vaporization. Two scenarios are possible, depending on the magnitude of annual precipitation relative to runoff threshold precipitation (P_rt ): (1) for P < P_rt , increases in annual precipitation lead to increases in runoff gain and proportionally larger increases in runoff; (2) for P > P_rt , increases in annual precipitation lead to decreases in runoff gain and proportionally smaller increases in runoff.

For semiarid regions P_rt ∕P_a ≈ 1. Therefore: (1) P < P_rt implies that P < P_a , and P > P_rt implies that P > P_a . We conclude the runoff is a strong competitor over vaporization in the case of greatest practical interest, i.e., in semiarid regions when the annual precipitation is below average. That is, in a semiarid region, a drop of rain is more likely to go to runoff on the dry side of the spectrum of annual rainfall (P < P_a ). Conversely, a drop of rain is more likely to go to vaporization on the wet side of the spectrum of annual rainfall (P > P_a ).

Unlike semiarid regions, for seasonally humid, humid, and subarctic regions P_rt ∕ P_a < 0.3. Therefore: (1) P < P_rt implies that P < 0.3 P_a , and (2) P > P_rt implies that P > 0.30 P_a . We conclude that vaporization is a strong competitor over runoff in humid regions (including seasonally humid and subarctic) when the annual precipitation is above 0.3 P_a . That is, in a humid region, a drop of rain is more likely to go to vaporization throughout a wide range of variation of annual rainfall (P > 0.3 P_a).

The competition between baseflow and vaporization follows a pattern similar to that of runoff and vaporization. In semiarid regions, baseflow is a strong competitor over vaporization on the dry side of the spectrum of annual rainfall (P < P_a ). In humid regions, vaporization prevails over baseflow throughout a wide range of variation of annual rainfall (P > 0.3 P_a ).

5.  SUMMARY

A conceptual model of water balance is used to simulate changes in runoff and baseflow with annual precipitation. The model in based on the sequential separation of annual precipitation into surface runoff and wetting, and wetting into basefiow and vaporization. The separation is modeled by a proportional relation such that wetting reaches asymptotically an upper bound as precipitation and surface runoff increase unbounded. Likewise, vaporization reaches asymptotically an upper bound as wetting and baseflow increase unbounded. The model parameters are the initial abstraction coefficient for surface runoff λ_s , the wetting potential W_p , the initial abstraction coefficient for baseflow λ_u , and the vaporization potential V_p .

Runoff gain is defined as the derivative of runoff coefficient with respect to precipitation. Baseflow gain is defined as the derivative of baseflow coefficient with respect to precipitation. Catchment data show that baseflow gains are always positive. Runoff gain reaches a peak for a runoff threshold precipitation; baseflow gain reaches a peak for a baseflow threshold precipitation.

Two runoff and baseflow functions are derived: (1) runoff and baseflow coefficients vs annual precipitation; (2) runoff and baseflow gains vs annual precipitation. The ratio of threshold precipitation P_t to mean annual precipitation P_a is shown to characterize the climatic setting, as follows: in semiarid regions, P_t ∕P_a is high, with values close to unity; in subhumid regions,P_t ∕P_a has midrange values, less than unity; in seasonally humid, humid, and subarctic regions, P_t ∕P_a has low values, generally less than or equal to 0.3.

Analysis of runoff and baseflow functions sheds additional light on the nature of the competition between runoff and vaporization, and baseflow and vaporization. Runoff and baseflow are shown to be strong competitors over vaporization in the case of greatest practical interes, i.e., in semiarid regions when the annual precipitation is below average (P < P_a ). On the other hand, vaporization is shown to be strong competitor over runoff and baseflow in humid regions throughout a wide range of variation of annual rainfall (P > 0.3 P_a).

ACKNOWLEDGMENTS

The present study was performed in Spring 1994, while A.V. Shetty was at San Diego State University, on leave from the Hard Rock Regional Centre, National Institute of Hydrology, Belgaum, Karnataka, India. His leave was funded by the United Nations Development Programme.

 REFERENCES

1. Baker, Jr., M. B. 1986. Effects of Ponderosa pine treatment on water yield in Arizona. Water Resour. Res., 22(1): 63-67.

2. Bosch, J. M. and J. D. Hewlett. 1982. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol., 55: 3-23.

3. Hibbert, A. R. 1967. Forest treatment effects on water yield. In: W.E. Sopper and H.W. Lull (Editors), International Symposium on Forest Hydrology. Pergarnon, Oxford.

4. L'vovich, M. I. 1979. World water resources and their future. Original in Russian. English translation, American Geophysical Union, Washington, DC.

5. Pitman, W. V. 1978. Trends in streamflow due to upstream land use changes. J. Hydrol., 39:227-237. .

6. Ponce, V. M. and A. V. Shetty. 1995. A conceptual model of catchment water balance: 1. Formulation and calibration. J. Hydrol., 173: 27-40.

7. Ruprecht, J. K. and N. J. Schofield. 1989. Analysis of streamflow generation following deforestation in southwest Western Australia. J. Hydrol., 105: 1-17

8. Ruprecht, J. K. and G. L. Stoneman. 1993. Water yield issues in the jarrah forest of southwestern Australia. J. Hydrol., 150: 369-391.

9. Shetty. A. V. 1994. Application of water balance conceptual model to the Malaprabha river basin, Karnataka. National Institute of Hydrology Report, Roorkee, Roorkee, Uttar Pradesh, India.