|
WHAT IS THE ASPECT RATIO OF A SELF-FORMED ALLUVIAL STREAM?
San Diego State University, San Diego,
California
1. INTRODUCTION
Alluvial streams are self-formed, i.e.,
their shape, characterized by depth and width, obeys the laws of mechanics,
properly within the field
of river mechanics. The ratio of width to depth is referred to as the aspect ratio of the Momentum integrates the acting force in time,
while energy integrates the same force in space; therefore,
they are not independent. In steady flow in open channels, the equations of mass and energy are used
to solve for the unknown flow variables (depth and slope).
In unsteady flow, the equations of mass and momentum are used for the same purpose.
This reality leaves the calculation of stream width out of fluid mechanics.
Lane and others (1959) developed a mechanistic approach to calculate the width in a self-formed channel.
The theory has been recently revisited by
Ponce and Jiang (2020). While Lane and others' approach
is limited to noncohesive materials under equilibrium conditions, it is a
point-of-start in the nascent field of
unsteady alluvial river mechanics.
The application of Lane's methodology may serve to
throw additional light onto relevant issues of floods, flood damages and related
sedimentation issues (ASCE, 1975; 2007). Moreover, in light of contemporary global climate change,
the subject is now becoming increasingly important.
2. LANE AND OTHERS' THEORY
The size of the cross-section for a stream channel in equilibrium, formed
with noncohesive materials, is dependent on the maximum threshold
discharge. Using principles of river mechanics,
The main assumptions used by Lane and others in deriving their theory are the following:
The side slope of the channel, at or above the water surface,
is equal to the friction angle φ of the noncohesive alluvial
material (Fig. 1).
The particles at the channel boundary are at the condition of incipient motion.
The lift and drag forces acting on each particle, together
with the downward component of the gravity force,
are balanced exactly by the frictional force developed between particles. The lift and
drag forces are assumed to be proportional to the tractive force exerted on the channel bottom. The
lift-to-drag force ratio is referred to as β.
The particles are held in place by virtue of their submerged weight resolved in a direction normal to the bed.
The tractive force acts in the direction of the flow and is equal to the weight of the column of water above the area on which the force acts.
The channel is assumed to be prismatic, with negligible secondary currents and the absence of backwater effects.
3. FINDINGS
The derivation of the Lane and others (1959)
theory has been extensively documented by
Ponce and Jiang (2020): Section 3.
In that report, Eq. 57, reproduced here as Eq. 1, is the equation derived by
in which To = channel top width, Yo = maximum (center) flow depth, φ = friction angle of the noncohesive material, β = lift-to-drag force ratio, and r = β tanφ.
Table 1 shows aspect ratios calculated using Eq, 1, for friction angle varying in
the range 5 ≤ φ ≤ 45°, at intervals of 5°,
and lift-to-drag-force ratio varying in the range -1 ≤ β ≤ 1, at intervals of 0.1.
For a typical value of φ = 30° and β = 0.4 (Apperley, 1968),
the aspect ratio is:
To / Yo = 5.86. Likewise,
4. ONLINE CALCULATION
Equation 1 may be solved with the aid of the online calculator
ONLINE LANE SHAPE.
For instance, for Yo = 1 m, φ = 30°, and β = 0.4,
the answer is: 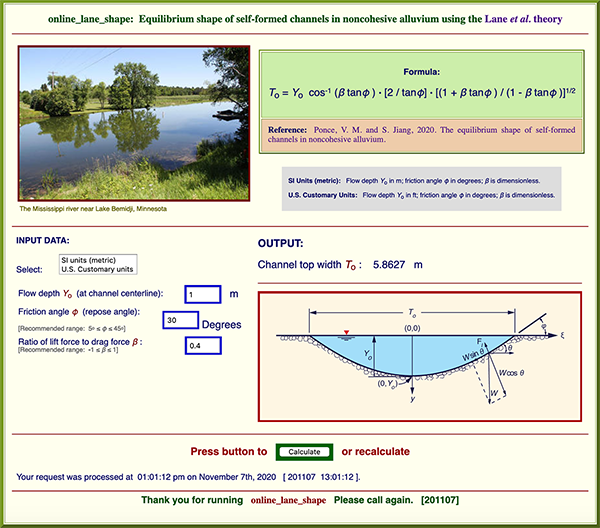
5. CONCLUDING REMARKS
The aspect ratio of a self-formed stream in noncohesive
alluvium has been calculated using the Lane and others (1959) theory.
The aspect ratio To /Yo is expressed in terms
of the friction angle φ of the material forming the channel bed and the
REFERENCES
Apperley, L. W. 1968. The effect of turbulence
on sediment entrainment. Thesis submitted
to the School of Engineering, University of
Auckland, Auckland, New Zealand, in partial fulfillment for the
requirements for the degree
of Doctor of Philosophy, January.
ASCE, 1975. Sedimentation Engineering. Manuals and Reports on Engineering Practice, Manual 54,
Vito A. Vanoni, editor, New York.
ASCE, 2007. Sedimentation Engineering: Processes, Measurements, Modeling, and Practice.
Manuals and Reports on Engineering Practice, Manual 110,
Marcelo H. Garcia, editor, New York.
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York.
Lane, E. W., P. N. Lin, and H. K. Liu. 1959.
The most efficient stable channel for comparatively clean water in noncohesive material.
Report CER-59HKL, Colorado State University, Fort Collins, Colorado, April.
Ponce, V. M., and S. Jiang. 2020.
The equilibrium shape of self-formed channels in noncohesive alluvium.
Online report.
Ponce, V. M. 2014.
Fundamentals of Open-channel hydraulics.
Online textbook. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 230924 |
