1.  INTRODUCCIÓN

Existe una necesidad urgente de tener mejores herramientas analíticas con las cuales evaluar la propagación de las perturbaciones del lecho en canales aluviales. La importancia de este esfuerzo se puede ver fácilmente en relación con el modelado de áreas de préstamo en ríos aluviales y estudios de degradación y degradación a largo plazo.

Gradowczyk (2) y Cunge y Perdreau (1), entre otros, han investigado la propagación de perturbaciones de lecho en su formulación unidimensional. Más recientemente, Ponce et al. (5) derivó una fórmula para la celeridad de las perturbaciones del lecho en función de parámetros hidráulicos y de transporte del material del lecho. Soni et al. (6) llevaron a cabo una serie de experimentos en un canal con el objetivo de estudiar las características del flujo. En este artículo, los datos de Soni et al. se utilizan para comprobar la validez de la teoría de Ponce et al.. Dada la limitada extensión de los datos, la comprobación experimental se considera preliminar, a la espera de estudios más detallados. No obstante, los resultados obtenidos son tales que justifican su presentación con la esperanza de estimular más investigaciones en esta área de la hidráulica de canales aluviales.

2.  TEORÍA

Ponce et al. (1979) realizó un análisis de estabilidad lineal sobre el conjunto de ecuaciones que gobiernan el flujo de agua y sedimentos en canales aluviales. Su análisis abordó flujos muy por debajo del estado crítico (por ejemplo, F ≤ 0.6), para los cuales la escala de tiempo de los fenómenos transitorios del lecho es varios órdenes de magnitud menor que los de la superficie del agua. Bajo estas condiciones, la suposición cuasi-estacionaria condujo a la siguiente fórmula para la celeridad de las perturbaciones de amplitud pequeña:

c*          Fo2(1 - Fo2)σ*2 c*(Φ)  =  ____ = __________________                 Φ         (1 - Fo2)2σ*2 + 9

(1)

en la cual Φ = parámetro de transporte de material del lecho (definido a continuación); c_*(Φ) = celeridad adimensional normalizada con el transporte; y c_*, σ_*, F_o son la celeridad adimensional, el número de onda adimensional y el número de Froude del flujo no perturbado, respectivamente, definidos de la siguiente manera:

c c*  =  _____             uo

(2)

2π                      2π            do σ*  =  ( ______ ) Lo  =  ( ______ ) ( _____ )                  L                        L             So

(3)

uo            Fo  =  _________             (g do)1/2

(4)

en la cual u_o = velocidad media del flujo no perturbado; d_o = profundidad de flujo; S_o = pendiente de fondo; L = longitud característica de la perturbación; L_o = longitud de referencia del canal; y g = aceleración de la gravedad.

La función de transporte de material del lecho se modela como una potencia de la velocidad media, de la siguiente manera:

gs  =  k um

(5)

en la cual g_s = tasa de transporte de material del lecho, por unidad de ancho; u = velocidad media; y k y m = coeficiente y exponente, respectivamente. Cuando la tasa de transporte del material del lecho se expresa en unidades de peso, el parámetro de transporte Φ es el siguiente:

m k uom-3            Φ  =  ___________             (1 - p) ρs

(6)

en la cual p = porosidad del material en el lecho; y ρ_s = densidad de masa de los sólidos.

En ciertos casos, es conveniente expresar la velocidad de transporte del material del lecho en términos de unidades volumétricas en lugar de unidades de peso. Esto conduce a la siguiente ecuación para Φ:

m k g uom-3            Φ  =  _____________                 (1 - p)

(7)

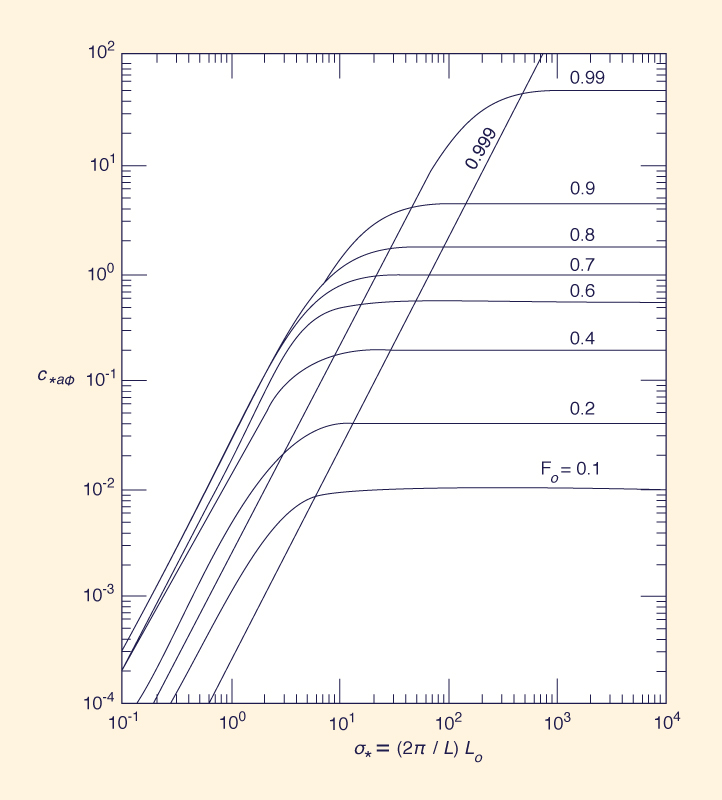
Se observa además que, para valores suficientemente grandes de σ_*, Ec. 1 se reduce a:

Fo2            c*(Φ)  =  _________                   1 - Fo2

(8)

haciendo el valor de c_*(Φ ) independiente de σ_* (Fig. 1). Dadas las Ecs. 1, 2 y 8, la expresión simplificada para la celeridad de las perturbaciones del lecho es:

Fig. 1  Celeridad adimensional normalizada por transporte c*( Φ), en función del número de Froude del flujo no perturbado Fo y el número de onda adimensional σ*.

Fig. 2  Perfiles promedio de la superficie del agua y del lecho transitorio, medidos por Soni et al. (6).

Fo2            c*  =  Φ uo __________                       1 - Fo2

(9)

aplicable para el caso de un tamaño de σ_* suficientemente grande.

3.  VERIFICACIÓN EXPERIMENTAL

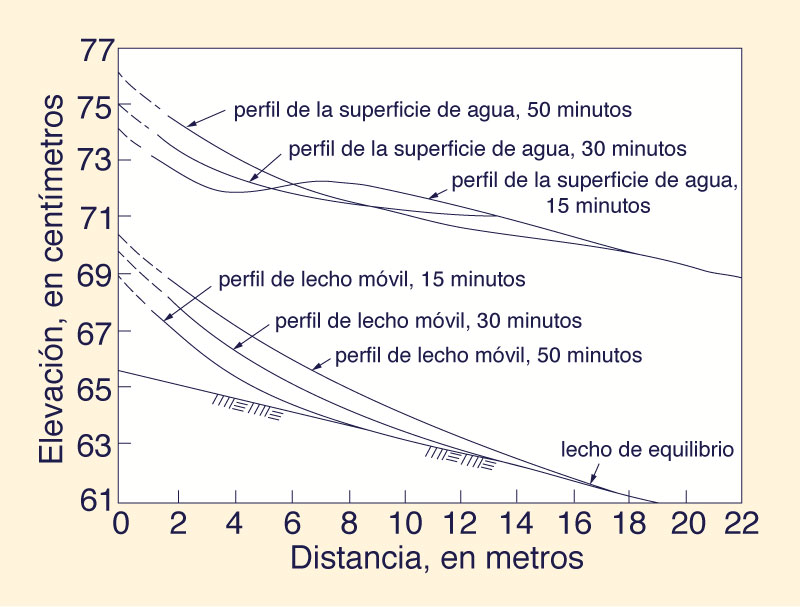
Los experimentos de Soni et al. (6) se utilizaron para comprobar la validez de la Ec. 1 y su versión reducida, Ec. 9. Para este propósito, los datos de la Fig. 3 en la Ref. 6 (mostrado aquí como Fig. 2), fue utilizado. Las características de flujo son las siguientes: u_o = 0.413 m/s; d_o = 0.086 m; y S_o = 0.00225. La ley de transporte de sedimentos se expresa mediante la Ec. 5, en la cual k = 0.00145; m = 5; y g está dado en metros cúbicos por segundo por metro.

Se asumió una porosidad típica: p = 0.4, lo que lleva, a través de la Ec. 7, a un valor de Φ = 0.02. La longitud característica de la perturbación (Fig. 2) se estimó en aproximadamente 20 m, a partir de la cual se calcula el número de onda adimensional de la siguiente manera:

2π        do σ*  =  _____ ( _____ )  =  12              L         So

(10)

Dado F_o = u_o/(gu_o)^1/2 = 0.45, σ_* = 12 se encuentra dentro del rango para el cual la celeridad es independiente de σ_*. Por lo tanto, la Ec. 9 es aplicable, lo que lleva a c_t = 0.0021 m/s como la velocidad teórica de propagación del lecho móvil que se muestra en la Fig. 2.

Para proporcionar una comparación significativa con los datos medidos, como se muestra en esta figura, se realizó una estimación de la velocidad de propagación de esta perturbación del lecho. La estimación consistió en medir la distancia, a lo largo del cauce, entre los perfiles de 15 y 30 minutos, y entre los perfiles de 30 y 50 minutos, en cinco elevaciones colocadas a intervalos de 0.005 m, comenzando a nivel del lecho. El promedio de 10 mediciones fue c_m = 0.0029 m/s, que se compara favorablemente con la celeridad teórica, c_t = 0.0021 m/s, calculado mediante la fórmula de Ponce et al. (1979).

La coincidencia es aún más cercana si se considera el hecho de que la celeridad teórica es estrictamente válida sólo para perturbaciones de pequeña amplitud. En base a experimentos numéricos, López García (3) ha determinado un factor de corrección α a aplicar a la celeridad teórica para tomar en cuenta la amplitud finita. Para F_o = 0.45, y tomando la relación entre la amplitud del lecho transitorio y la profundidad de flujo uniforme, z_o /d_o, como aproximadamente 0.2 para el presente caso, el valor de α según López García (3) es α = 1.2. Por lo tanto, la celeridad teórica, corregida por efectos de amplitud finita, es c_t = 0.0025 m/s.

En vista de la variabilidad inherente en la mecánica del transporte de sedimentos y la dificultad de medir con precisión el movimiento de los sedimentos, los resultados de la comparación anterior son sorprendentes. De manera similar, dicho acuerdo, cuando se comparan las celeridades teóricas y medidas del lecho, ha sido documentado por Ponce y Mahmood (1976).

4.  RESUMEN Y CONCLUSIONES

La aplicabilidad de una fórmula para el cálculo de la celeridad del lecho móvil de un canal aluvial se ha verificado utilizando datos experimentales. La fórmula es fácil de usar, con la celeridad expresada en términos de parámetros hidráulicos y de transporte de sedimentos fácilmente identificables. Los resultados obtenidos son alentadores y muestran la promesa de este enfoque en el análisis cualitativo de la hidráulica de lecho móvil. La necesidad de investigación adicional en esta área es reconocida.

BIBLIOGRAFÍA

1. Cunge, J. A., y N. Perdreau. 1973. "Bed Fluvial Mathematical Models", La Houille Mutile Blanche, No. 7, Grenoble, France.

2. Gradowczyk, M. H. 1968. "Wave Propagation and Boundary Instability in Erodible Chennels", Journal of Fluid Mechanics, Vol. 33, Part 1, pp. 93-112.

3. López García, J. 1977. "Mathematical Modeling of Alluvial Channel Bed Transients", thesis presented to Colorado State University, Fort Collins, Colo., in parcial fulfillment of the requirements for the degree of Master of Science.

4. Ponce, V. M., y K. Mahmood. 1976. "Meandering Thalwegs in Straight AlIuvial Channel". Rivers 76, Proceedings of the Third Annual Symposium of the Waterways, Harbors and Coastal Engineering Division, ASCE, Vol. 2, Aug., pp. 1418-1441.

5. Ponce, V. M., H. Indlekofer, y D. B. Simons. 1979. "The Convergence of Implicit Bed Transient Models", Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY4, Proc. Paper 14493, Apr., pp. 351-363.

6. Soni, J. P., R. J. Gante, y Ranga Raju, K. G. 1977. "Nonuniform Flow in Aggrading Channels", Journal of the Waterway, Port, Coastal and Ocean Division, ASCE, Vol, 103, No. WW3. Proc. Paper 13151. Aug., pp, 321-333.