1.  INTRODUCTION

There is an urgent need for improved analytical tools with which to assess the propagation of bed perturbations in alluvial channels. The importance of this endeavor may be seen readily in connection with the modeling of borrow pits in alluvial rivers and studies of long-term aggradation and degradation.

Gradowczyk (2) and Cunge and Perdreau (1), among others, have researched the propagation of bed perturbations in its one-dimensional formulation. More recently, Ponce et al. (5) derived a formula for the celerity of bed perturbations as a function of hydraulic and bed material transport parameters. Soni et al. (6) carried out a series of flume experiments with the objective of studying flow characteristics in aggrading channels. Herein, the Soni et al. data is used to check the validity of the Ponce et al. theory. Given the limited extent of the data, the experimental check is regarded as preliminary, pending more detailed studies. Nevertheless, the results obtained are such that they warrant presentation in the hope of stimulating further research in this area of alluvial channel hydraulics.

2.  THEORETICAL BACKGROUND

Ponce et al. (1979) performed a linear stability analysis on the set of equations governing the flow of water and sediment in alluvial channels. Their analysis dealt with flows well below the critical state (say, F ≤ 0.6), for which the time scale of the bed transients is several orders of magnitude smaller than that of the water surface transients. Under these conditions, the quasi-steady assumption led to the following formula for the celerity of small bed perturbations:

c*          Fo2(1 - Fo2)σ*2 c*(Φ)  =  ____ = __________________                 Φ         (1 - Fo2)2σ*2 + 9

(1)

in which Φ = bed material transport parameter (defined below); c_*(Φ) = transport-normalized dimensionless celerity; and c_*, σ_*, F_o are the dimensionless celerity, dimensionless wave number, and Froude number of the unperturbed flow, respectively, defined as follows:

c c*  =  _____             uo

(2)

2π                      2π            do σ*  =  ( ______ ) Lo  =  ( ______ ) ( _____ )                  L                        L             So

(3)

uo            Fo  =  _________             (g do)1/2

(4)

in which u_o = unperturbed mean flow velocity; d_o = unperturbed flow depth; S_o = bed slope; L = characteristic length of the perturbation; L_o = reference channel length; and g = gravitational acceleration.

The bed material transport function is modeled as a power of mean velocity, as follows:

gs  =  k um

(5)

in which g_s = bed material transport rate per unit of channel width; u = mean flow velocity; and k and m = coefficient and exponent, respectively. When the bed material transport rate is expressed in terms of units of weight, the transport parameter Φ is given as follows:

m k uom-3            Φ  =  ___________             (1 - p) ρs

(6)

in which p = porosity of the material in the channel bed; and ρ_s = mass density of solids.

In certain cases, it is convenient to express the bed material transport rate in terms of volumetric units rather than weight units. This leads to the following equation for Φ:

m k g uom-3            Φ  =  _____________                 (1 - p)

(7)

It is further noticed that, for sufficiently large values of σ_*, Eq. 1 reduces to:

Fo2            c*(Φ)  =  _________                   1 - Fo2

(8)

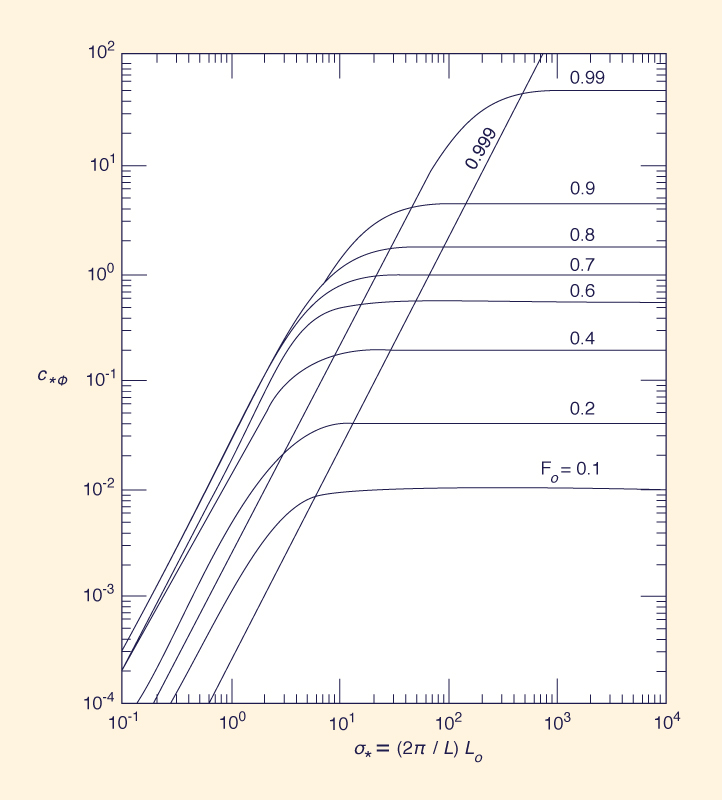
making the value of c_*(Φ) independent of σ_* (Fig. 1). Given Eqs. 1, 2, and 8, the simplified expression for the celerity of bed perturbations is:

Fig. 1  Transport-normalized dimensionless celerity of bed perturbations c*(Φ), as a function of the unperturbed flow Froude number Fo and the dimensionless wave number σ*.

Fo2            c*  =  Φ uo __________                       1 - Fo2

(9)

applicable for the case of a sufficiently large σ_*.

3.  EXPERIMENTAL VERIFICATION

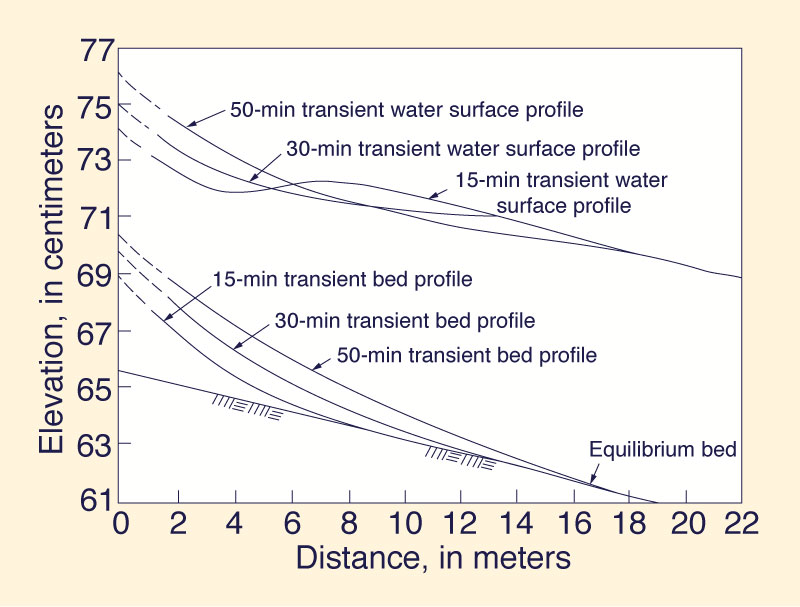
The flume experiments of Soni et al. (6) were used to check the validity of Eq. 1 and its reduced version, Eq. 9. For this purpose, the data of Fig. 3 in Ref. 6 (shown here as Fig. 2), was used. The flow characteristics are given as follows: u_o = 0.413 m/s; d_o = 0.086 m; and S_o = 0.00225. The sediment transport law is expressed by Eq. 5, in which k = 0.00145; m = 5; and g is given in cubic meters per second per meter.

Fig. 2  Average transient bed and water surface profiles, as measured by Soni, et al. (6).

A typical porosity was assumed: p = 0.4, leading through Eq. 7 to a value of Φ = 0.02. The characteristic length of the perturbation (Fig. 2) was estimated to be approx 20 m, from which the dimensionless wave number is calculated as follows:

2π        do σ*  =  _____ ( _____ )  =  12              L         So

(10)

Given F_o = u_o/(gu_o)^1/2 = 0.45, σ_* = 12 lies within the range for which the celerity is independent of σ_*. Therefore, Eq. 9 is applicable, leading to c_t = 0.0021 m/s, as the theoretical velocity of propagation of the bed transient shown in Fig. 2.

In order to provide a meaningful comparison with the measured data, as depicted in this figure, an estimate of the velocity of propagation of this particular bed disturbance was made. The estimate consisted of measuring the distance along the channel between the 15- and 30-minute profiles, and between the 30- and 50-minute profiles, at five elevations positioned at 0.005-m intervals, starting at bed level. The average of 10 measurements was c_m = 0.0029 m/s, which compares favorably with the theoretical celerity, c_t = 0.0021 m/s, calculated by the Ponce et al. formula.

The agreement is even closer if attention is drawn to the fact that the theoretical celerity is strictly valid only for small amplitude perturbations. Based on numerical experiments, Lopez-Garcia (3) has determined a correction factor α to be applied to the theoretical celerity in order to account for the finite transient amplitude. For F_o = 0.45, and taking the ratio of bed transient amplitude to the uniform flow depth, z_o/d_o, as approximately 0.2 for the present case, the value of α according to Lopez-Garcia (3) is α = 1.2. Therefore, the theoretical celerity corrected for finite amplitude effects is c_t = 0.0025 m/s.

In view of the inherent variability in sediment transport mechanics and the difficulty of accurately measuring sediment motion, the results of the above comparison are indeed remarkable. Similarly, such agreement when comparing theoretical and measured bed transient celerities has been documented elsewhere (4).

4.  SUMMARY AND CONCLUSIONS

The applicability of a formula for the calculation of celerity of alluvial channel bed transients has been verified using data from flume experiments. The formula is easy to use, the celerity is expressed in terms of readily identified hydraulics and sediment transport parameters. The results obtained are encouraging, and show the promise of this approach in the qualitative analysis of unsteady alluvial channel hydraulics. The need for additional research in this area is recognized.

REFERENCES

1. Cunge. J. A., and N. Perdreau. 1973. "Bed Fluvial Mathematical Models", La Houille Mutile Blanche, No. 7, Grenoble, France.

2. Gradowezyk, M. H. 1968. "Wave Propagation and Boundary Instability in Erodible Chennels", Journal of Fluid Mechanics, Vol. 33, Part 1, pp. 93-112.

3. Lopez-Garcia, J. 1977. "Mathematical Modeling of Alluvial Channel Bed Transients", thesis presented to Colorado State University, Fort Collins, Colo., in partial fulfillment of the requirements for the degree of Master of Science.

4. Ponce. V. M., and K. Mahmood. 1976. "Meandering Thalwegs in Straight AlIuvial Channel". Rivers 76, Proceedings of the Third Annual Symposium of the Waterways, Harbors and Coastal Engineering Division, ASCE, Vol. 2, Aug., pp. 1418-1441.

5. Ponce, V. M., H. Indlekofer, and D. B. Simons. 1979. "The Convergence of Implicit Bed Transient Models", Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY4, Proc. Paper 14493, Apr., pp. 351-363.

6. Soni, J. P., R. J. Gante, and Ranga Raju, K. G. 1977. "Nonuniform Flow in Aggrading Channels", Journal of the Waterway, Port, Coastal and Ocean Division, ASCE, Vol, 103, No. WW3. Proc. Paper 13151. Aug., pp, 321-333.