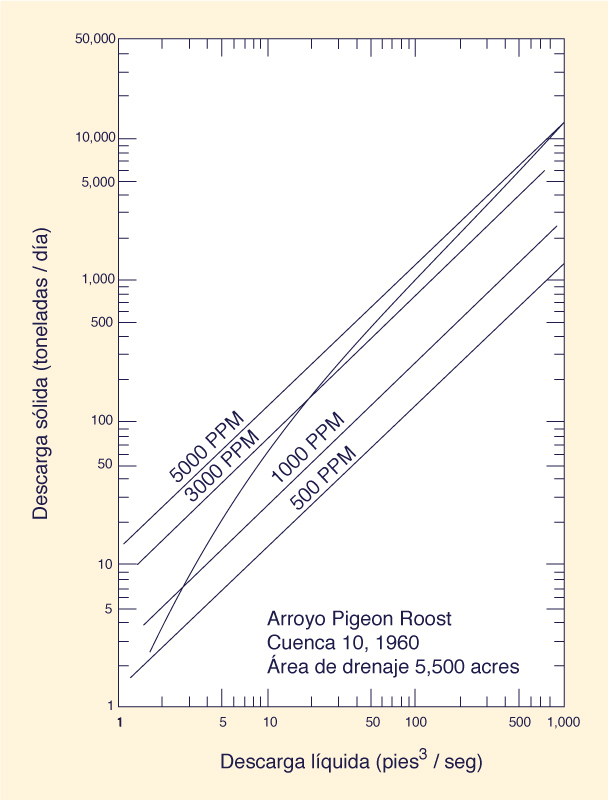
1.  INTRODUCCIÓN

En la práctica de la ingeniería hidráulica, la curva de gasto de sedimentos se utiliza para relacionar la descarga de sedimentos (caudal sólido) con la descarga de agua (caudal líquido), en condiciones de flujo permanente, o de equilibrio. La pendiente de la curva de gasto de sedimentos es una medida de la concentración de sedimentos suspendidos del material del lecho. En este artículo, la concentración de sedimentos suspendidos del material del lecho se denomina "concentración de sedimentos", y específicamente excluye la carga de lavado (wash load).

Por lo general, las curvas de gasto de sedimentos trazadas en escala logarítmica tienen pendientes grandes para caudales bajos y pendientes pequeñas para caudales altos, como se muestra en la Fig. 1 (1). Para un caudal suficientemente alto, la pendiente de la curva de gasto de sedimentos se aproxima asintóticamente al valor de uno (1), es decir, una concentración constante de sedimentos del material del lecho. Esta concentración constante de sedimentos que las corrientes tienden a alcanzar con caudales altos se denomina aquí "concentración última de sedimentos". Como se muestra en este artículo, la concentración última de sedimentos se puede calcular fácilmente en función de las propiedades del flujo y del sedimento.

2.  CONCENTRACIÓN ÚLTIMA DE SEDIMENTOS

En la práctica de la ingeniería hidráulica, la siguiente función se usa comúnmente para proporcionar un ajuste entre los datos de caudal sólido y líquido:

Qs  =  c Q m

(1)

en la cual Q_s = descarga de sedimentos suspendidos, o caudal sólido, Q = caudal líquido, y c y m, coeficiente y exponente de la curva de gasto, respectivamente.

En la Ecuación 1, para m = 1, la concentración de sedimentos es independiente de Q e igual a lo siguiente:

Cs'  =  c

(2)

en la cual C_s' = concentración final de sedimentos. El valor de m = 1 parece ser un valor mínimo al que se aproximan las corrientes, con caudales muy altos (Ref. 1, p. 476).

Una fórmula de transporte de sedimentos ampliamente utilizada, la cual está basada en el método de Colby (2) es la siguiente:

qs  =  k ρ v n

(3)

en la cual q_s = descarga de sedimentos, por unidad de ancho; v = velocidad media; k = parámetro, una función de las propiedades del sedimento del material del lecho, incluido el tamaño medio de las partículas, la gradación y la gravedad específica; ρ = densidad del agua; y n = exponente. El valor de n suele estar en el rango 3 ≤ n ≤ 7.

Colby (2) ha demostrado que los valores altos de n prevalecen para caudales bajos, mientras que los valores bajos de n son típicos de caudales altos. Debido a que n no puede disminuir de manera realista por debajo del valor de 3, n = 3 se toma como el exponente asociado a la concentración última del sedimento. En este caso, la configuración del lecho se acerca al régimen superior (upper regime) (por ejemplo, lecho plano con movimiento de sedimentos), en el que la fricción de fondo se debe en gran parte a la rugosidad del grano (5).

Con n = 3, la Ecuación 3 es dimensionalmente homogénea:

qs  =  k ρ v 3

(4)

en la cual q_s = descarga última de sedimentos, por unidad de ancho, y k es un parámetro adimensional.

El caudal, por unidad de ancho es:

q  = v d

(5)

en la cual d = profundidad de flujo.

En términos de descarga por unidad de ancho, la Ec. 2 se reformula como sigue:

qs Cs  =  ______               q

(6)

La sustitución de las Ecs. 4 y 5 en la Ec. 6 conduce a lo siguiente:

Cs  = k F 2 γ

(7)

en la cual:

γ  = ρ g

(8)

es el peso específico del agua, g = aceleración de la gravedad, y

v F  =  ___________            (gd )1/2

(9)

es el número de Froude del flujo permanente.

La Ecuación 7 se puede utilizar en modo de calibración o de predicción. En el modo de calibración, se conocen el número de Froude y la concentración final del sedimento, y la Ec. 7 se utiliza para resolver el parámetro k. En el modo de predicción, F y k son conocidos, y la Ec. 7 se usa para resolver C_s'. Por ejemplo, con k = 0.1, y F = 0.2, la Ec. 7 conduce a:

C_s' = 0.1 × 0.04 × 1,000 g/L = 4 g/L = 4,000 ppm.

Para canales hidráulicamente anchos, se puede derivar una ecuación alternativa a la Ec. 7. La siguiente expresión relaciona la pendiente de fricción (o de fondo) con el número de Froude, en condiciones de flujo permanente (es decir, flujo uniforme en el caso de canales artificiales) (3):

So  = f  F 2

(10)

en la cual S_o = pendiente de fondo, y

g f  =  ______           C 2

(11)

en la cual f = factor de fricción adimensional de Chezy, y C = coeficiente de Chezy. Combinando las Ecs. 7 y 10 se obtiene:

k So Cs'  =  ________ γ                 f

(12)

Dada la Ecuación 12, la concentración última de sedimentos se puede calcular como una función de los siguientes tres parámetros adimensionales: (1) parámetro de transporte de sedimentos k, (2) pendiente de fondo S_o, y (3) factor de fricción f. Por ejemplo, con C = 70 m^1/2/s, S_o = 0.0084, y k = 0.05, la aplicación de las Ecs. 11 y 12 conduce a lo siguiente: C_s' = 10,000 ppm.

En la práctica, el parámetro k es una medida de la capacidad del flujo para arrastrar y transportar sedimentos del material del lecho. No sólo tiene en cuenta el tamaño medio de las partículas, la gradación y la gravedad específica, sino también el efecto de la concentración de la carga de lavado y la temperatura del agua en el transporte del material del lecho (2).

3.  RESUMEN Y CONCLUSIONES

Con caudales suficientemente altos, las curvas de gasto de sedimentos muestran una tendencia asintótica hacia una concentración constante de sedimentos (material de lecho suspendido). Este valor máximo de concentración de sedimentos se denomina aquí concentración última de sedimentos.

Se muestra que la concentración última de sedimentos es una función de un parámetro adimensional de transporte de sedimentos (de material del lecho) y un parámetro adimensional del flujo (el cuadrado del número de Froude). Alternativamente, el número de Froude al cuadrado se puede expresar como la relación entre la pendiente fondo y el factor de fricción de Chezy adimensional.

Fig. 1   Curva típica de gasto de sedimentos (1). 4.  APLICACIONES La Ecuación 7 puede usarse para el cálculo de la concentración de sedimentos suspendidos del material del lecho, aplicable para caudales altos. Por ejemplo, se necesita una fórmula de transporte de sedimentos aplicable a caudales altos en el cálculo de rupturas graduales de presas de tierra, ya sea postuladas o retrospectivas. El parámetro de transporte de sedimentos k puede utilizarse como parámetro de calibración, a determinar en función de los datos de concentración última de sedimentos, o alternativamente, en un modo de predicción, una vez que se haya establecido su valor. A la fecha, la experiencia sugiere que k está normalmente restringido dentro de un rango relativamente pequeño (4). Las curvas de gasto de sedimentos, bajo una amplia gama de caudales, son relativamente escasas (Ref. 1, p. 476). Por lo tanto, para comprender la gama de caudales altos, a menudo son necesarias extrapolaciones. Las extrapolaciones que no toman en cuenta la concentración última de sedimentos están destinadas a dar como resultado valores muy altos de descarga de sedimentos. En casos extremos, la descarga de sedimentos extrapolada de esta manera puede resultar en una concentración superior a 1,000,000 ppm, lo que es claramente imposible. Por lo tanto, es necesaria investigación adicional para aclarar los mecanismos físicos que gobiernan la aproximación a la concentración última de sedimentos. APÉNDICE I.  BIBLIOGRAFÍA ASCE. 1975. "Sedimentation Engineering," Manual No. 54. Colby, B. R. 1964. "Discharge of sands and mean velocity relations in sand-bed streams," Profeasional Paper No. 462-A, U.S. Geological Survey, Washington, D.C. Lighthill, M. J., y G. B. Whitham. 1955. "On kinematic waves. I. Flood movement in long rivers," Proceedings of the Royal Society of London, Vol. A229, May, pp. 281-216. Ponce, V. M., y A. J. Tsivoglou. 1981. "Modeling gradual dam breaches," Journal of the Hydraulics Division, ASCE, Vol. 107, No. HY7, July, pp. 829-838. Simons, D. B. y E. V. Richardson. 1966. "Resistance to flow in alluvial channels," Professional Paper 422-J, Washington, U.S. Geological Survey, Washington, D.C. APÉNDICE II.  NOTACIÓN En este artículo se utilizan los siguientes símbolos: C = coeficiente de Chezy; Cs' = concentración última de sedimentos (material del lecho suspendido); c = coeficiente de curva de gasto de sedimentos; d = profundidad de flujo; F = número de Froude del flujo permanente; f' = factor de fricción adimensional de Chezy; g = aceleración de la gravedad; k = parámetro de transporte de sedimentos (material de lecho suspendido) ; m = exponente de la curva de gasto de sedimentos; n = exponente de la fórmula de descarga de sedimentos; Q = caudal líquido; Qs = caudal sólido (material de lecho suspendido); q = caudal líquido unitario; qs = caudal sólido unitario (material de lecho suspendido); qs' = descarga última de sedimentos (material de lecho suspendido), por unidad de ancho; So = pendiente de fricción o de fondo; v = velocidad media; γ = peso específico del agua; y ρ = densidad del agua.