1. INTRODUCCIÓN
La característica esencial de un modelo numérico es el reemplazo de una derivada tal como ∂ƒ/∂s por una relación de diferencias finitas tal como Δƒ/Δs. Al hacerlo, el modelo numérico debe satisfacer ciertos requisitos de estabilidad y convergencia. La estabilidad se refiere a la capacidad del esquema numérico para inhibir la amplificación de errores. La convergencia es una medida del tamaño del error de discretización.
En la práctica, la estabilidad es una condición necesaria para el funcionamiento del modelo, ya que un modelo inestable tiene poca o ninguna utilidad. En los modelos numéricos, la estabilidad generalmente se logra a expensas de la convergencia. Por lo tanto, la convergencia es el tema central: Una vez que se demuestra que el modelo es estable, es necesario evaluar sus propiedades de convergencia.
El método de von Neumann (5) para el análisis sistemático de la estabilidad y la convergencia ha sido reconocido en la literatura hidráulica (8) como una poderosa herramienta analítica para estudiar las propiedades de los modelos numéricos. En el presente artículo, este método se aplica para estudiar las propiedades de convergencia de modelos numéricos implícitos transitorios de lecho móvil en canales aluviales. Cunge y Perdreau (2), Mahmood y Ponce (4) y Ponce et al. (7) han desarrollado modelos numéricos de propagación transitoria de lecho móvil. Cunge y Perdreau estudiaron las propiedades numéricas de su modelo, pero no llegaron a generalizar sus hallazgos con respecto a la fricción de borde y el transporte de sedimentos. El análisis que se presenta en este artículo muestra que es posible aislar los parámetros de fricción y transporte de sedimentos, proporcionando así una mayor comprensión de las propiedades de convergencia de los modelos numéricos implícitos transitorios de lecho móvil.
2. ECUACIONES DE GOBIERNO
Las ecuaciones que gobiernan el flujo en un canal aluvial unidimensional son: (1) Continuidad del agua; (2) continuidad de sedimentos; y (3) ecuación del movimiento. Expresadas por unidad de ancho de canal, tienen la siguiente forma:
Continuidad del agua:
Continuidad de sedimentos:
Ecuación de movimiento:
en las cuales: u = velocidad media; h = elevación de la superficie del agua; z = elevación del fondo del canal;
Se necesitan dos ecuaciones complementarias que describan la fricción del fondo y el transporte de material de fondo. La fricción de fondo se puede expresar mediante una relación de tipo Chézy, de la siguiente forma:
en la cual ƒ = factor de fricción adimensional, definido como sigue:
y C = coeficiente de Chézy. Para flujo uniforme, el esfuerzo cortante de fondo es:
De igual manera:
en la cual So = pendiente de fondo. Por lo tanto, a partir de las Ecs. 6 y 7 se obtiene:
en la cual Fo = número de Froude del flujo uniforme, definido como sigue:
La velocidad de transporte del material de fondo se modela mediante una relación de tipo Colby (1) de la siguiente forma:
en la cual k y m son parámetros empíricos de transporte de material de fondo.
3. ECUACIONES SIMPLIFICADAS
En el flujo subcrítico de régimen bajo (Fo ≤ 0.6), las ondas transitorias del lecho se propagan aguas abajo con una celeridad que es varias órdenes de magnitud menor que la de las ondas de la superficie. Esta diferencia de escala de tiempo permite la solución para las ondas del lecho asumiendo una descarga constante dentro de un intervalo de tiempo, reduciendo así el problema a dos ecuaciones (continuidad de sedimentos y ecuación de movimiento) en dos incógnitas (nivel de la superficie del agua y nivel del lecho de la corriente). Además, para Fo ≤ 0.6, el término de concentración espacial en la Ec. 2 es pequeño en comparación con los términos restantes (4);
Sustituyendo la Ec. 10 en la Ec. 2, y expresando u en términos de q y d:
Operando en la Ec. 11:
Sustituyendo la Ec. 10 en la Ec. 12:
Dividiendo por u ( 1 - p ) ρs g:
en la cual cb = concentración de material del lecho en partes por unidad, definida como sigue:
En la Ecuación 14, expresando u en términos de q y d, y d en términos de h y z:
Sustituyendo la Ecuación 4 en la Ecuación 3:
En la Ecuación 17, expresando u en términos de q y d, y d en términos de h y z:
4. ANÁLISIS DE ESTABILIDAD LINEAL
Las Ecuaciones 16 y 18 deben satisfacer tanto el flujo de equilibrio para el cual h = ho, z = zo,
La sustitución de las variables perturbadas en la Ec. 16 conduce a la siguiente ecuación:
en la cual:
De las Ecuaciones 9, 10 y 15:
Por lo tanto:
en la cual Φ = parámetro compuesto de transporte de material de lecho, definido como sigue:
Sustituyendo la Ec. 22 en la Ec. 19:
La sustitución de las variables perturbadas en la Ec. 18 conduce a lo siguiente:
en la cual:
5. SOLUCION ANALÍTICA
La solución del sistema de Ecs. 24 y 25 se postula en forma exponencial como sigue:
y
en las cuales:
y
en las cuales L = longitud de onda; T = período de onda; y h* y z* son funciones adimensionales de amplitud.
La celeridad adimensional, c*, de una perturbación sinusoidal se define como sigue (6):
El decremento logarítmico, δ, se define de la siguiente manera (6):
La sustitución de las Ecs. 27 y 28 en las Ecs. 24 y 25 dan como resultado un sistema homogéneo de ecuaciones lineales en las incógnitas h* y z*. La condición no trivial para el determinante de la matriz de coeficientes conduce a una celeridad adimensional normalizada de transporte, c*aΦ, expresada como sigue:
y un decremento logarítmico, δa, expresado como sigue:
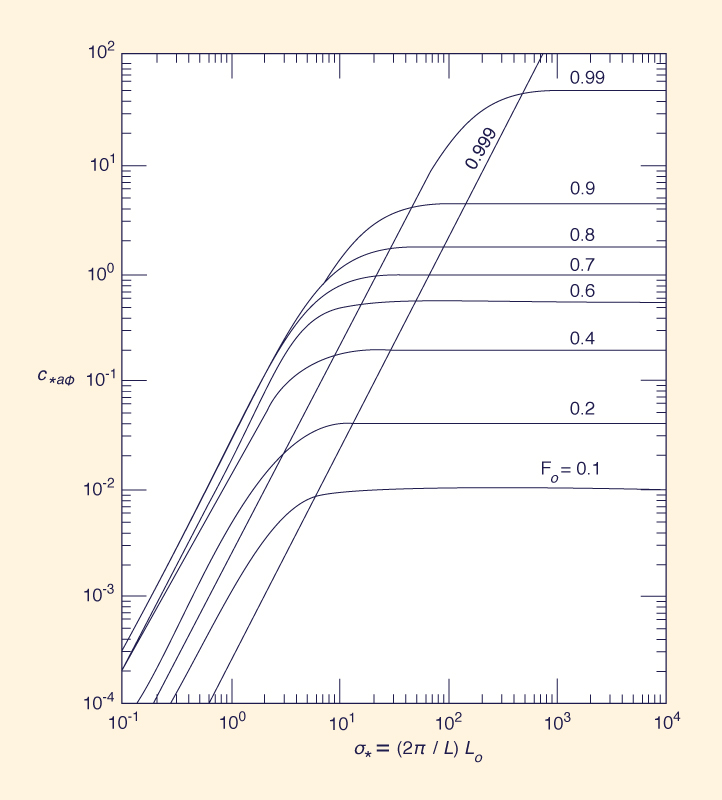
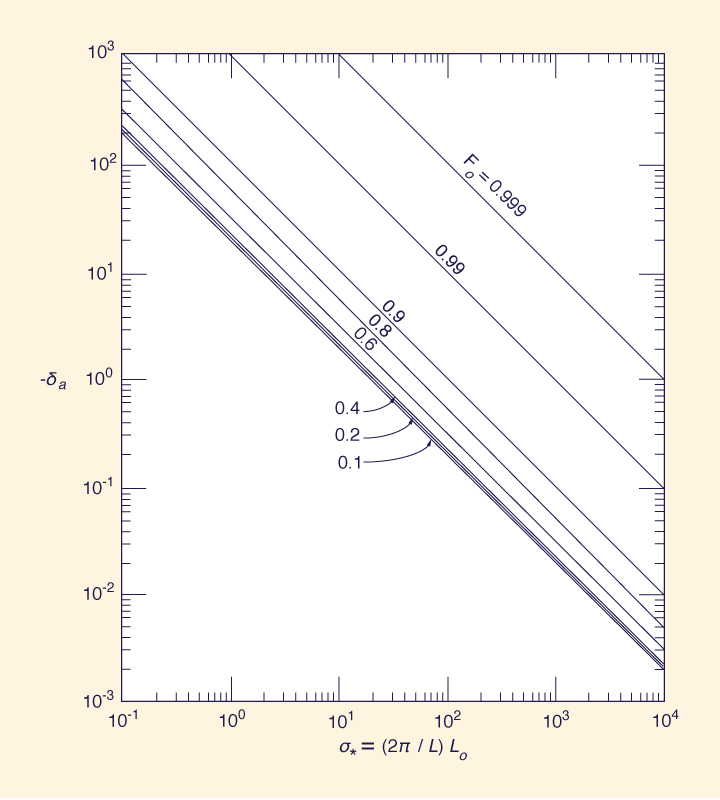
Las Figuras 1 y 2 muestran la celeridad adimensional normalizada por transporte, c*aΦ, y el decremento logarítmico, δa, en función del número de Froude del flujo de equilibrio, Fo, y el número de onda adimensional, σ*, en flujo subcrítico.
6. SOLUCIÓN NUMÉRICA
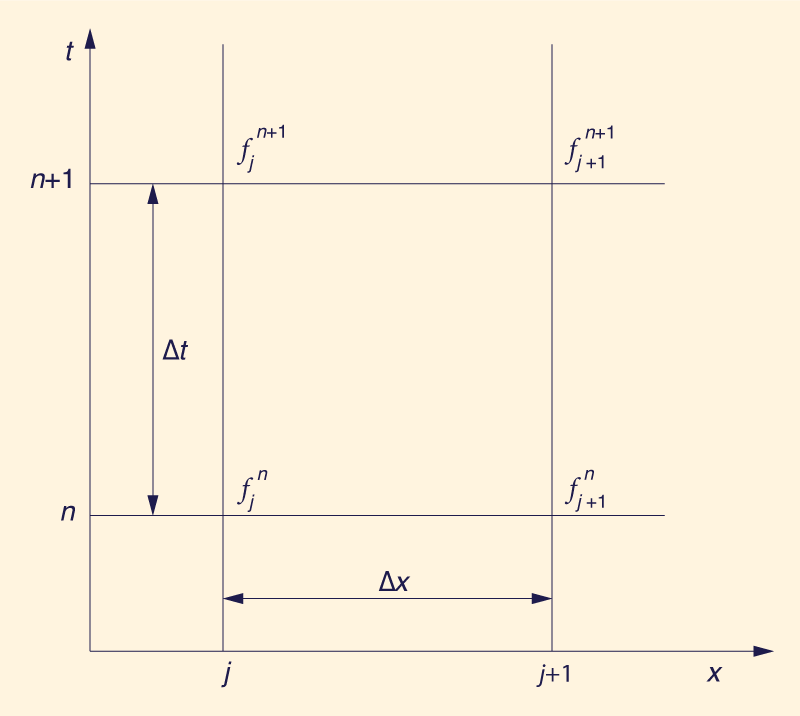
El esquema implícito de cuatro puntos de Preissmann (3) se utiliza para discretizar las ecuaciones de gobierno. Las ecuaciones en diferencias finitas tienen la siguiente forma (Fig.3):
en las cuales ƒ(x,t) = variable dependiente; Δx = intervalo de espacio; Δt = intervalo de tiempo; y Llamando η = h' y ζ = z', las Ecs. 24 y 25 se convierten a:
Sustituyendo las Ecs. 39-41 en 42 y 43 se obtiene:
La sustitución de las Ecs. 27 y 28 en las Ecs. 44 y 45 conduce a lo siguiente:
en las cuales:
y
Las Ecuaciones 46 y 47 conducen a un sistema homogéneo de ecuaciones lineales con las incógnitas h* y z*. Para que la solución no sea trivial, el determinante de la matriz de coeficientes debe anularse. Esto conduce a:
en la cual C = número de Courant del lecho, definido como sigue:
Dado que:
la Ecuación 52 se reduce a:
Resolviendo la Ec. 55 para E:
en la cual:
En la Ecuación 56, expresando β* en sus componentes reales e imaginarios:
Se obtiene:
y
La celeridad adimensional de la solución numérica, c*n, se define como sigue:
Dado que:
y definiendo:
la Ecuación 63 se reduce a:
El decremento logarítmico de la solución numérica, δn, es definido como sigue:
Las Ecuaciones 66 y 67 permiten el cálculo de la celeridad de propagación, c*nΦ, y decremento logarítmico, δn, del esquema numérico implícito de cuatro puntos de las Ecs. 2 y 3, en función de: (1) Número de Froude del flujo de equilibrio, Fo = uo / (gdo)1/2; (2) número de onda adimensional, σ*, del componente transitorio del movimiento, σ* = (2π /L)Lo; (3) parámetro de resolución espacial,
7. ANÁLISIS DE CONVERGENCIA
El análisis de convergencia se basa en las siguientes ralaciones:
El valor R1 es la relación de atenuación, y R2 es la relación de translación (fase). Para (δn - δa) > 0, R1 > 1, lo cual conduce a amplificación numérica; para (δn - δa) < 0, R1 < 1, lo cual conduce a una atenuación numérica. Para R2 > 1, la translación numérica es mayor que la translación física; para R2 < 1, la translación numérica es menor que la translación física. Para R1 = R2 = 1, existe una coincidencia exacta entre la soluciones analíticas y numéricas.
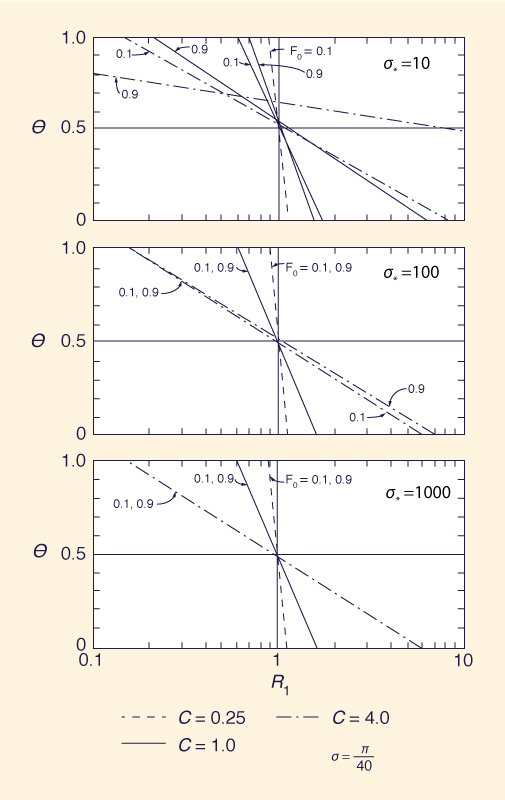
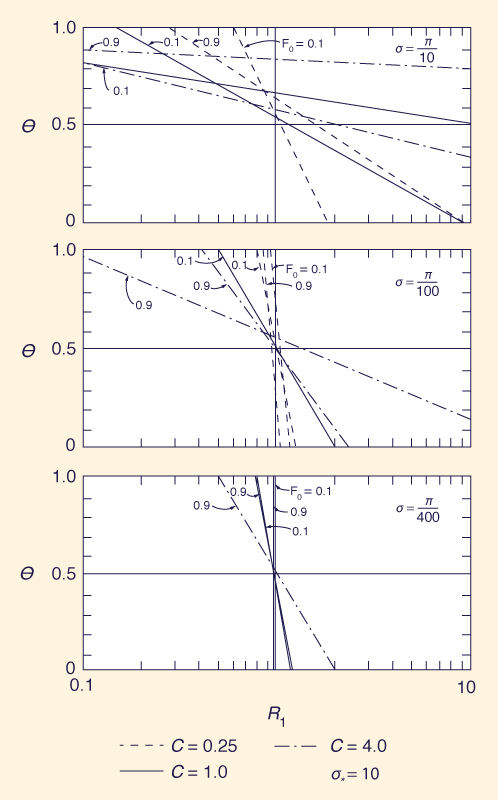
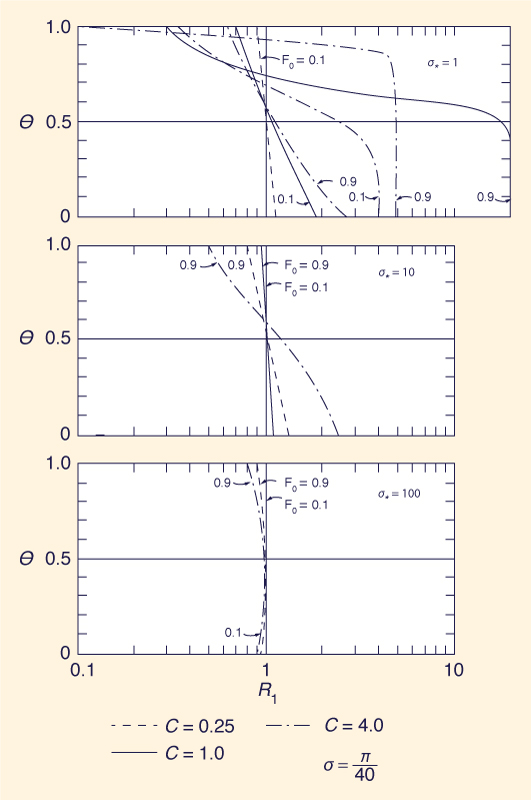
Las Figuras 4 y 5 muestran la relación de atenuación, R1, como una función de Fo, σ*, α, C y θ.
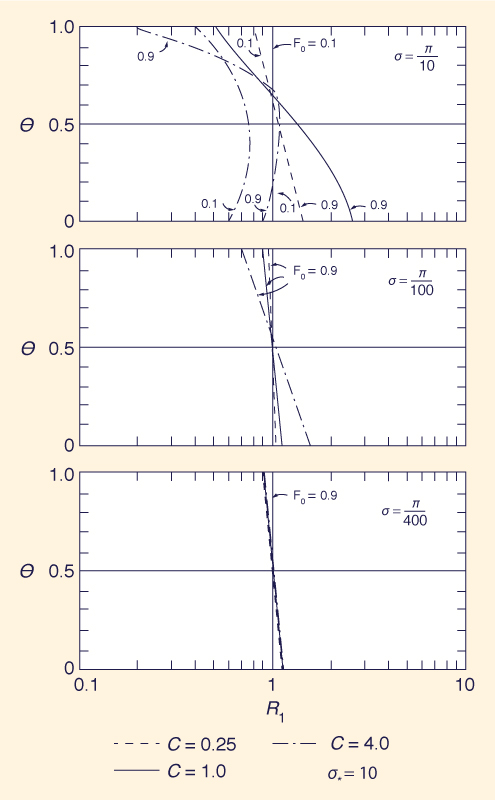
Las Figuras 6 y 7 muestran la relación de translación, R2, en función de Fo, σ*, α, C y θ.
Los resultados de las Figs. 4-7 permiten obtener las siguientes conclusiones: (1) La convergencia mejora para un valor suficientemente alto de σ*, y para valores bajos de Fo, α, y C; y (2) para un valor de θ en el rango medio, entre 0.5 y 1, satisfacerá en general los requisitos de estabilidad y convergencia. Con base en el análisis realizado, se recomienda el siguiente rango de parámetros: σ* ≥ 10; Fo ≤ 0.6;
En la práctica, σ y Fo están determinadas por las características del problema siendo considerado. Los valores recomendados para α, C, y θ deben tomarse solo como una sugerencia.
8. RESUMEN Y CONCLUSIONES
Se presenta un tratamiento teórico detallado de la convergencia del modelo numérico implícito transitorio de lecho móvil. Se calcula la celeridad adimensional y el decremento logarítmico de las soluciones analíticas y numéricas. La convergencia se prueba estableciendo la relación de celeridades (convergencia de translación) y de las relaciones de atenuación (convergencia de atenuación). Se identifican dos parámetros físicos y tres numéricos, a saber: el número de Froude del flujo de equilibrio Fo, el número de onda adimensional del flujo transitorio σ* , la resolución espacial α, el número de Courant C, y el factor de ponderación θ.
AGRADECIMIENTOS
La investigación presentada en este documento fue apoyada en parte por la Estación Experimental de la Universidad Estatal de Colorado. La visita de Horst Indlekofer a la Universidad Estatal de Colorado fue posible gracias a una beca de la OTAN.
APÉNDICE Ι. BIBLIOGRAFÍA
Colby, B, R. 1964. "Discharge of Sands and Mean Velocity Relationships in Sand-Bed Streams," Professinal Paper 462-A, United States Geological Survey, Washington, D.C.
Cunge, J. A., y N. Perdreau. 1973. "Mobile Bed Fluvial Mathematical Models," La Houille Balanche, Grenoble, France, No. 7, 561-580.
Liggett, J. A., y J. A. Cunge. 1975. "Numerica Methods of Solution of the Unsteady Flow Equations," Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Fort Collins, Colo., 89-182.
Mahmood, K., and V. M. Ponce. 1976. "Mathematical Modeling of Sedimentation Transients in Sand-Bed Channels," Report CER75-76-KM-VMP28, Engineering Research Center, Colorado State University, Fort Collins, Colo., Apr.
O'Brien, G. G., M. A. Hyman, and S. Kaplan. 1951. "A study of the Numerical Solution of Partial Differential Equations," Journal of Mathematics and Physics, Vol. 29, No. 4, 223-251.
Ponce, V. M., y D. B. Simons. 1977. "Shallow Wave Propagation in Open Channel Flow," Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12. Proc. Paper 13392, Dec., 1461-1476.
Ponce, V. M., J. Lopez Garcia, y D. B. Simons. 1979. "Modeling Alluvial Channel Bed Transients," Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY3. Proc. Paper 14456, Mar., 245-256.
Roache, P. J. 1972. Computational Fluid Dynamics, Hermosa Publishers, Albuquerque, N. M.
APÉNDICE ΙΙ. SIMBOLOGÍA
En este artículo se utilizan los siguientes símbolos:
Ao = parámetro, Ec. 20;
C = coeficiente de Chézy, y número Courant de lecho móvil;
ca = celeridad analítica;
cb = concentración de material del lecho, Ec. 15;
cn = celeridad numérica;
c* = celeridad adimensional, Ec. 35;
c*a = celeridad analítica adimensional;
c*n = celeridad numérica adimensional;
c*aΦ = celeridad analítica adimensional normalizada de transporte, Ec. 37;
c*nΦ = velocidad numérica adimensional normalizada de transporte, Ec. 66;
d = profundidad de flujo;
E = parámetro, Ec. 48;
F = número de Froude;
ƒ = factor de fricción adimensional, Ec. 5 y variable dependiente;
g = aceleración de la gravedad;
gs = tasa de transporte de material del lecho de ancho unitario;
h = elevación de la superficie del agua;
j = índice de discretización espacial;
k = parámetro empírico de transporte de material del lecho, Ec. 10;
L = longitud de onda;
Lo = longitud del canal, Ec. 34;
M = parámetro, Ec. 57;
m = parámetro empírico de transporte de material del lecho, Ec. 10;
N = parámetro, Ec. 58;
n = índice de discretización de tiempo;
P = parámetro, Ec. 59;
p = porosidad del material del lecho;
q = descarga de agua, por unidad de ancho;
R1 = relación de atenuación, Ec. 68;
R2 = relación de translación (fase), Ec. 69;
So = pendiente de fondo;
T = período de la onda;
t = variable temporal;
u = velocidad media;
x = variable espacial;
z = elevación de fondo;
α = parámetro de resolución espacial, Ec. 51;
β*I = factor de atenuación (o amplificación);
β*R = frecuencia adimensional, Ec. 30;
Δt = intervalo de tiempo;
Δx = intervalo de espacio;
δ = decremento logarítmico, Ec. 36;
δa = decremento logarítmico de la solución analítica, Ec. 38;
δn = decremento logarítmico de solución numérica, Ec. 67;
ζ = elevación de la perturbación de fondo;
η = perturbación de la elevación de la superficie del agua;
θ = factor de ponderación del esquema implícito;
ρs = densidad de sólidos;
ρw = densidad del agua;
σ* = número de onda adimensional, Ec. 29;
τb = esfuerzo cortante de fondo;
Φ = parámetro compuesto de transporte de material de lecho, Ec. 23;
Subíndices
o = flujo de equilibrio;
* = variable adimensional; y
Superíndice
' = variable perturbada.
|
| 220101 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |