1. INTRODUCCIÓN Los métodos simplificados de enrutamiento de avenidas disfrutan de una posición de preeminencia dentro de la gama de métodos de enrutamiento disponibles. Estos métodos son sencillos de formular y utilizar, y bien pueden explicar la mayoría de los fenómenos de las ondas de inundación en lo referente a aplicaciones prácticas. Las versiones más refinadas simulan el modelo de onda difusiva y en esto radica su ventaja.
Un método simplificado que está recibiendo mayor atención es el método de Muskingum en el cual los parámetros de enrutamiento se calculan en función de las características hidráulicas del canal y las de la malla (1), en este documento denominado modelo difusivo de Muskingum-Cunge. Una consecuencia directa de la resolución espacial insuficiente son los notorios caudales negativos que se han documentado en algunos casos (3,10). Mientras no se identifique la causa de esta anomalía, los métodos simplificados adolecerán de falta de credibilidad. Esto sólo puede obstaculizar su aceptación para aplicaciones prácticas. El objetivo de este artículo es, por lo tanto: (1) revisar y examinar las contribuciones recientes sobre resolución espacial y temporal en el modelo difusivo de Muskingum-Cunge; y (2) desarrollar un criterio de resolución espacial para preservar la exactitud del método. Aquí se entiende por exactitud lo que se puede lograr dentro del marco del enrutamiento de ondas difusivas. 2. CONTRIBUCIONES RECIENTES Koussis (2) fue uno de los primeros en reconocer el efecto de una resolución espacial insuficiente en el hidrograma calculado por el modelo difusivo de Muskingum-Cunge y en vincular este efecto al tamaño de la malla. Propuso, "para obtener resultados razonables", la siguiente restricción:
en el cual Δt = intervalo de tiempo; Δx = intervalo de espacio; X = parámetro; y c = celeridad de la onda de inundación. Koussis no dio más detalles sobre cómo la Ec. 1 fue obtenida, y se atribuye aquí a su experiencia con el método. Weinman y Laurenson (10), en su reciente revisión de métodos aproximados de enrutamiento de ondas de inundación, se enfocan en el modelo difusivo de Muskingum-Cunge y sus variantes. Señalan la posibilidad de salidas negativas poco realistas, pero sugieren que, para efectos prácticos, éstas son lo suficientemente pequeñas y de corta duración como para ser ignoradas si se satisface la siguiente desigualdad:
en el cual Tr = tiempo de crecida del hidrograma.
Es evidente la sorprendente similitud entre los criterios de Koussis y Weinman y Laurenson.
lo que indica que el criterio de Koussis es más conservador en la estimación de Δx que el de Weinmann y Laurenson. Los autores (7) han informaron los resultados de los hallazgos preliminares que parecían indicar que si se debe preservar la precisión (es decir, evitar las salidas negativas), la siguiente desigualdad debe mantenerse:
en el cual C y D son números de Courant y de Reynolds de la malla, respectivamente, definidos de la siguiente manera:
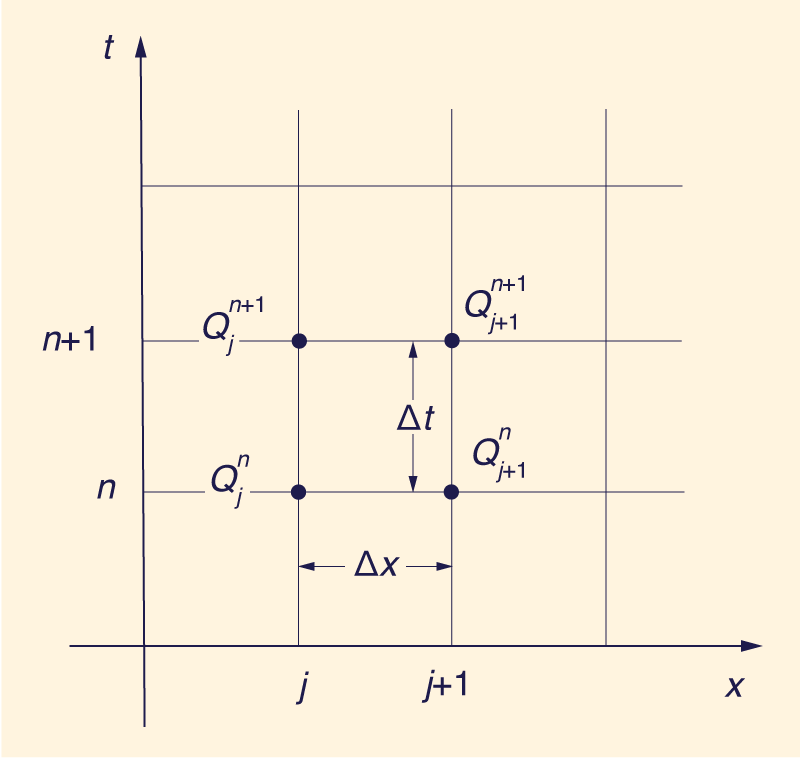
en el cual qo = caudal de referencia por unidad de ancho; y So = pendiente de equilibrio de la superficie de agua. Además Ponce y Theurer afirmaron que un valor de ξ = 0.25 proporcionaba una precisión satisfactoria en la mayoría de los casos. Kundzewicz (3) aplicó el método de análisis de convolución al modelo de onda difusiva de Muskingum y concluyó que la Ec. 2 no es válida para el caso general. Además, afirmó que la búsqueda de un criterio general para suprimir las salidas negativas podría resultar infructuosa. 3. INTERVALOS DE ESPACIO Y DE TIEMPO Los criterios de precisión como las Ecs. 1, 2 o 4 proporcionan pautas para la selección de intervalos de espacio y tiempo si el objetivo es eliminar los flujos de salida negativos. De acuerdo a Ponce y Yevjevich (5), los intervalos de espacio y tiempo se utilizan junto con los propiedades hidráulicas y de la onda de inundación para calcular los parámetros de enrutamiento C y D, es decir, las Ecs. 5 y 6. A su vez, estos parámetros se utilizan en la ecuación de enrutamiento (Fig. 1):
en la cual C1, C2 and C3 se definen como sigue:
Intervalo de espacio. Dadas las Ecs. 1, 2 y 4, la elección del intervalo de espacio no está del todo clara. Un límite superior para Δx es ciertamente una necesidad en cualquier procedimiento numérico y el presente método no es una excepción. La Ecuación 1 parecería indicar que el límite superior debería ser el siguiente:
Sin embargo, esta condición adolece de un inconveniente; no está definida para X = 0. En el enrutamiento de onda difusiva de Muskingum, X = 0 implica que Δx es fijo, y la Ec. 11 ya no podría ser aplicable. El mismo tipo de crítica se aplica a la Ec. 2. Por otro lado, la Ec. 4 se expresa en términos de D en lugar de X, y la expresión para el límite superior de Δx basada en esta ecuación es:
La cuestión de un límite inferior para Δx también ha provocado cierta confusión, principalmente debido a la existencia de una relación entre X y Δx:
Históricamente, el parámetro X se ha interpretado como un factor de ponderación, y esto llevó a Miller y Cunge (4), entre otros, a sugerir un límite inferior para X: X ≥ 0. Este concepto se repite en la revisión de Weinmann y Laurenson (10), que establece lo siguiente (p. 1529): Dado que X no puede disminuir de manera realista por debajo de cero, existe un límite para el grado permisible de subdivisión, lo que implica un límite inferior para Δx. Dada la Ec. 13, este límite inferior se puede calcular estableciendo X ≥ 0, a partir del cual:
El lado derecho de la Ec. 14 se reconoce inmediatamente como la "longitud característica de un tramo" identificada por primera vez por Kalinin y Milyukov (4) en relación con el método de enrutamiento que lleva su nombre. Sin embargo, la experiencia con el método ha demostrado que, de hecho, no existe un límite inferior teórico para Δx. Ponce y Theurer (7), así como otros investigadores (3,9), han informado de la experiencia con valores de Δx que infringen la Ec. 14, y sin embargo, sin irrealidad física alguna adjunta a los resultados del cálculo.
La razón de este comportamiento es evidente cuando se reconoce la característica de igualación del momento en la Ec. 13. Siempre que se satisfaga esta ecuación, Δx puede elegirse arbitrariamente para infringir la Ec. 14, lo que implica la posibilidad de valores negativos de X. Intervalo de tiempo. El criterio para seleccionar el intervalo de tiempo también ha generado alguna confusión. Un límite superior en Δt es claramente una necesidad si la solución debe permanecer dentro de un marco numérico razonable. A diferencia de la resolución espacial, la resolución temporal es un concepto más fácil de comprender en aplicaciones hidrológicas, ya que los hidrogramas se representan en el dominio temporal. La práctica establecida es establecer un límite superior para Δt tal que se cumpla la siguiente desigualdad:
en la cual n = número entero que tiene un valor mínimo de 5. En la práctica, los hidrogramas están sesgados hacia la derecha; por lo tanto, la Ec. 15 garantiza un nivel satisfactorio de resolución temporal. Además del requisito de resolución temporal, existe la duda de si el modelo difusivo de Muskingum está sujeto al criterio de estabilidad numérica de Courant que normalmente se aplica a los problemas hiperbólicos. Si éste es el caso, entonces se debe imponer una restricción adicional sobre Δt:
que proviene de la siguiente relación:
Los cálculos prácticos, sin embargo, han demostrado que las infracción de las Ecs. 16 y 17 no dan lugar a inestabilidad numérica. Este comportamiento se explica recordando que el método es esencialmente una formulación en diferencias finitas de la ecuación de la onda cinemática. Un límite inferior en Δt es principalmente una cuestión de recursos computacionales. La decisión sobre este asunto se deja al modelador. Criterios de precisión. Del análisis anterior, se deduce que no existe una justificación teórica para un límite inferior para Δt o Δx. Además, aunque existe un límite superior para Δt dado por el requisito de resolución temporal, un límite superior similar para Δx no es claramente discernible. Dadas las Ecs. 5, 6 y 13, el criterio de Koussis se modifica aquí y se expresa en términos de C y D:
De esta forma, la sobredeterminación de la Ec. 11 se elimina. En efecto, para X = 0, D = 1 y El criterio de Weinmann y Laurenson, Ec. 3, conduce a:
y se aplican comentarios similares a los de Koussis. El criterio de Ponce y Theurer continua siendo:
La siguiente sección describe un programa de experimentos numéricos diseñado para arrojar luz adicional sobre la cuestión de los criterios de precisión. Consistencia. Estrechamente relacionado con la precisión está el tema de la consistencia de un método de enrutamiento simplificado como el presente. En el contexto de este estudio, la precisión se refiere a evitar salidas negativas físicamente irreales; de otro modo, la consistencia se refiere a la capacidad del método para producir los mismos resultados independientemente del tamaño de la malla. Por ejemplo, si se obtiene un determinado hidrograma al final de un tramo dado usando diez (10) intervalos de espacio, un método consistente produciría el mismo hidrograma si en cambio sólo se hubieran usado dos (2) intervalos. La consistencia se utilizará en el marco de un método de enrutamiento simplificado en el que el objetivo es optimizar la difusión numérica haciéndola coincidir con la difusión física. Este concepto no debe confundirse con la propiedad de consistencia de un esquema convencional de diferencias finitas, en el que el objetivo es minimizar la cantidad de error numérico para resolver adecuadamente la ecuación diferencial en consideración. 4. EXPERIMENTOS NUMÉRICOS
Se llevó a cabo un programa de experimentos numéricos con el fin de evaluar la precisión (y por ende, la consistencia) del enrutamiento de difusión de Muskingum descrito por las Ecs. 7-10.
Se probaron seis canales hipotéticos. Para cada canal, se especificaron dos condiciones de flujo: (1) Un flujo base bajo; y (2) un flujo base alto. Cada canal y condición de flujo se probó calculando el mismo hidrograma a través de doce (12) especificaciones de la malla, lo que hace un total de 144 corridas. Las doce (12) especificaciones de la malla representaron combinaciones de tres intervalos de tiempo y cuatro intervalos de espacio. Para simular hidrogramas naturales, se utilizó una distribución gamma como hidrograma de entrada. Esta función tiene la siguiente forma:
en la cual Qt = flujo de entrada en el tiempo t; Qb = flujo base; Qp = flujo pico; tp = tiempo desde el inicio de la escorrentía directa hasta el pico del hidrograma; tg = tiempo desde el inicio de la escorrentía directa hasta el centro de gravedad del hidrograma; y m está dado por la siguiente ecuación:
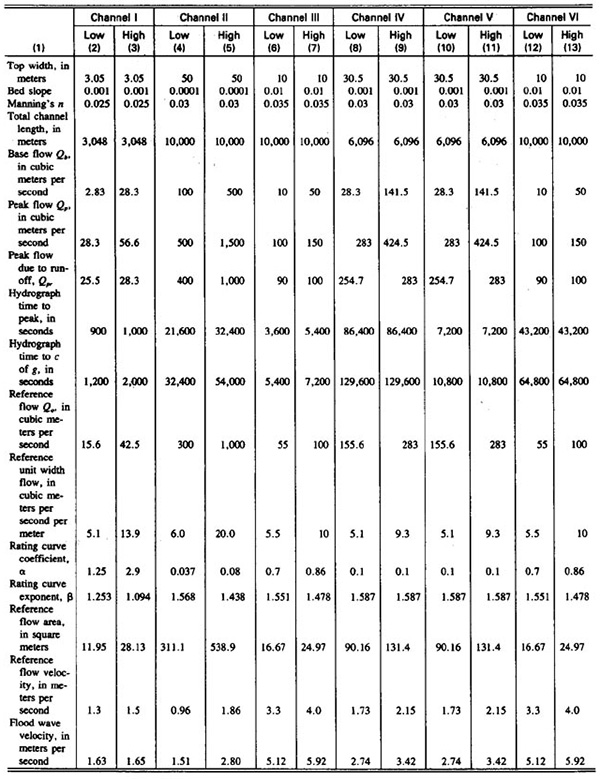
La Tabla 1 muestra las características del canal y del hidrograma para las doce (12) series de ensayos.
5. ANÁLISIS DE RESULTADOS
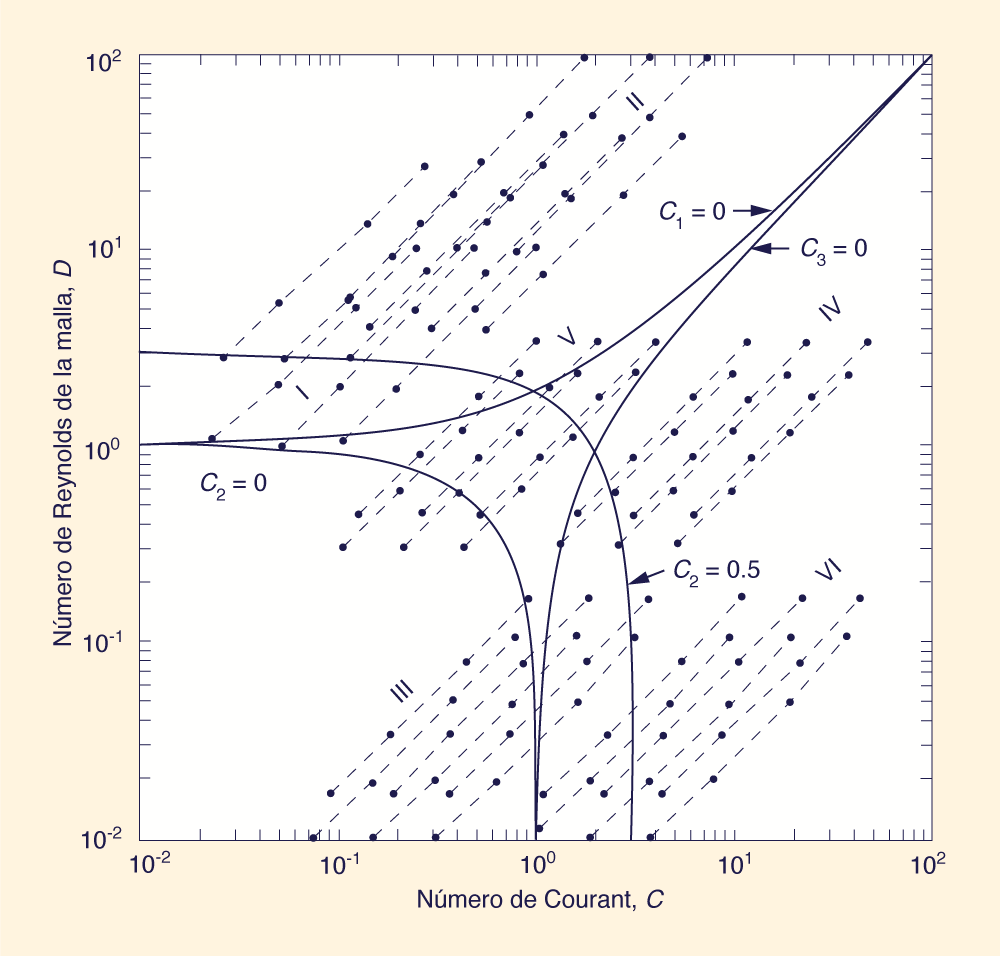
Los resultados de los experimentos numéricos pueden ser interpretados a la luz de los dos parámetros de enrutamiento: número Courant, C, y el número de Reynolds de la malla, D. La Figura 2 es un gráfico logarítmico de los valores de C y D asociados con los resultados del programa de ensayos. En esta figura también se muestran las líneas para C1 = 0, C2 = 0, y C3 = 0. Un análisis de los resultados numéricos indica claramente que la precisión depende del valor de C2. Los valores negativos de C2 están asociados invariablemente con caídas en la parte ascendente del hidrograma de flujo de salida, lo que indica la tendencia de los flujos de salida a volverse "negativos" (es decir, valores menores que el flujo base). Esta tendencia aumenta a medida que aumenta el valor de C2 en el rango negativo.
Los valores de C2 en el rango 0.0-0.5 no muestran caídas en el hidrograma de salida. Sin embargo, dependiendo del problema, aún pueden permanecer pequeñas inexactitudes en los hidrogramas calculados. Los valores de C2 superiores a 0.5 están asociados con hidrogramas que no muestran ninguna de las anomalías anteriores. Además, una vez que se alcanza la precisión, digamos para C2 ≥ 0.5, se garantiza las consistencia. En otras palabras, los hidrogramas calculados en el rango C2 ≥ 0.5 muestran una excelente reproducibilidad del flujo máximo, el tiempo al pico y la forma del hidrograma, con la variación de Δx y Δt. 6. CRITERIOS DE PRECISIÓN EN LA RESOLUCIÓN ESPACIAL
La evidencia experimental sugiere que C2 y sólo C2 es determinante de la precisión. De hecho, los valores de C1 y C3 fueron monitoreados a lo largo de la serie de ensayos, y se demostró que los valores negativos para cualquiera de ellos no afecta la precisión del hidrograma calculado. La condición C2 ≥ 0 se examina más a fondo aquí. Esto conduce, con la Ec. 9, a C + D ≥ 1, que es el criterio de Koussis modificado desarrollado en la sección anterior. Una condición más fuerte viene dada por C2 ≥ 0.5, lo que conduce a
En general, se aplica una condición tal que C2 ≥ ζ , en la cual ζ es un número real positivo.
Es instructivo examinar el significado físico de este criterio. Dadas las Ecs. 5 y 6, la Ec. 24 se puede expresar de la siguiente manera:
en la cual:
es la longitud de Courant, definida como la longitud del canal recorrida por la onda de crecida en un intervalo de tiempo Δt; y
en la "longitud característica del tramo", definida en términos de la fricción y sección transversal del canal. Además, se observa que:
en la cual uo = velocidad media del flujo; y do = profundidad del flujo; y
en la cual β = exponente de la relación caudal-área de flujo Q = α Aβ, de la cual:
Dadas las Ecs. 29 y 30, la Ec. 24 alternativamente se puede expresar de la siguiente manera:
en la cual β, uo, do, y So = propiedades del canal y del flujo; y κ = un parámetro de precisión determinado experimentalmente. Un valor de κ = 2 es suficiente para preservar la precisión para aplicaciones prácticas. 7. RESUMEN Y CONCLUSIONES Se lleva a cabo un análisis del enrutamiento de difusión de Muskingum. Se realizan experimentos numéricos para arrojar luz adicional sobre el criterio que establece un límite superior al intervalo espacial Δx con el fin de preservar la precisión. La experiencia computacional indica que para valores muy grandes de Δx, existe una tendencia a que ocurran flujos negativos, los cuales son físicamente irreales. Los resultados de los experimentos numéricos indican que el valor de C2 es determinante de la precisión. La condición C2 ≥ ζ es postulada para preservar la precisión (y consistencia) del método de enrutamiento, en el que ζ es un número real positivo. Esto conduce a un límite superior para Δx dado por la siguiente relación:
Se recomienda un valor de ζ = 0.33, el cual corresponde a κ = 2. Las cantidades ΔxC y ΔxD se definen en términos de características de canal y tamaño de la malla. AGRADECIMIENTOS
La investigación en la cual se basa este documento fue financiada en parte por el Servicio de Conservación de Suelos (SCS), Departamento de Agricultura de los EE.UU., Lanham, Maryland. APÉNDICE I. BIBLIOGRAFÍA
APÉNDICE II. NOTACIÓN
Los siguientes símbolos son usados en el siguiente artículo:
A = área de flujo;
C = número de Courant, Ec. 5;
C1 = coeficiente de enrutamiento, Ecs. 7 y 8;
C2 = coeficiente de enrutamiento, Ecs. 7 y 9;
C3 = coeficiente de enrutamiento, Ecs. 7 y 10;
c = celeridad de la onda de inundación;
D = número de Reynolds de la malla, Ec. 6;
do = profundidad de flujo;
j = índice espacial;
m = exponente, definido por la Ec. 22;
n = índice espacial, número entero en la Ec. 3;
Q = caudal;
Qb = flujo base;
Qp = flujo pico;
Qt = flujo de entrada en el instante t;
qo = caudal por unidad de ancho;
So = pendiente de equilibrio del flujo de agua;
Tr = período de crecida del hidrograma de entrada;
t = tiempo;
tg = tiempo desde el inicio de la escorrentía directa hasta el centro de gravedad del hidrograma;
uo = velocidad media del flujo;
X = parámetro de Muskingum;
α = coeficiente en la relación Q = α A β;
β = exponente en la relación Q = α A β;
Δt = intervalo de tiempo;
Δx = intervalo de espacio;
ΔxC = longitud de Courant;
ΔxD = longitud característica del tramo;
ξ = parámetro de precisión, Ec. 4;
κ = parámetro de precisión, Ecs. 24 y 25; y
ζ = número real positivo, en la Ec. 24.
|
| 220709 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |