|
Abstract. The hydraulic design of a channel transition is described and explained.
The calculation of an inlet transition between canal and flume is shown by an example,
originally presented by Hinds (1928)
and subsequently cited by Chow (1959). The example is reproduced
with detailed explanation and minor corrections for rounding accuracy.
An online calculator is provided.
|
1. INTRODUCTION
A transition is an open-channel flow structure whose purpose is to change the shape or cross-sectional area of the flow.
The design objective is to avoid excessive energy losses and to minimize surface waves and other turbulence.
When the transition is designed to keep the streamlines smooth and parallel, the theory of gradually varied flow is applicable.
In practice, the design of channel transitions is based
on the principles of energy and momentum conservation.
The form or shape of a transition may vary from as simple as straight-line headwalls normal to the flow to very elaborate
streamlined warped structures. Straight-line headwalls are often satisfactory for small canal structures or
where there is plenty of available hydraulic head (Fig. 1).
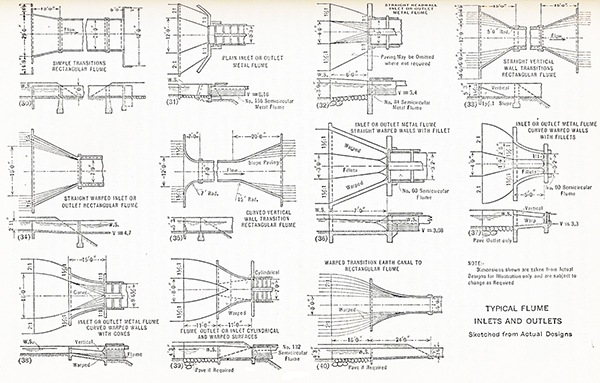
Other simplifications may be applied as long as they do not cause excessive wave action or turbulence (Fig. 2).
Fig. 1 A simple channel transition.
Common types of transitions are inlet and outlet transitions between: (1) canal and flume, (2) canal and tunnel, and (3)
canal and inverted siphon. Appreciable changes in flow depth within the transition may lead to rapidly varied flow
and the generation of standing waves.
| [Click on figure to display] |
Fig. 2 Typical flume inlets and outlets (Hinds, 1928).
2. DESIGN PROCEDURE
Careful consideration should be given to the detail dimensions of the transition
throughout its entire length. The design water-surface profile
should be a smooth, continuous curve,
tangent to the water-surface profile upstream and downstream of the transition.
The occurrence of critical flow or hydraulic jump should
be avoided.
A curved transition should be used in all
important designs.
The best approach is to first select the shape of the water surface
and then to calculate the dimensions of the
cross sections to conform with established principles of conservation of energy.
Transition between canal and flume, or canal and tunnel
The following design features are considered (Hinds, 1928; Chow, 1959):
Length and angle. A well-designed transition should follow these rules:
A sharp angle should be avoided to minimize the possibility of standing waves.
The optimum angle subtended between the channel axis and a line connecting the
channel sides between entrance and exit sections is 12.5°.
Losses. The energy loss through a transition has two components:
Conversion loss, which is generally expressed in terms of the change
in velocity head between the entrance and exit sections of the
transition structure. Table 1 shows conversion loss coefficients for transitions.
Friction loss, which may be estimated by the use of a uniform flow formula. This loss is usually very small and may be considered to be negligible for preliminary design.
Table 1 Conversion loss coefficients for transitions.
|
| Type of transition |
Inlet coefficient ci |
Outlet coefficient co |
| Warped |
0.10 |
0.20 |
| Cylinder quadrant |
0.15 |
0.25 |
| Simplified straight line |
0.20 |
0.30 |
| Straight line |
0.30 |
0.50 |
| Square ended |
0.30 + |
0.75 |
|
Water-surface profile.
The drop in water-surface elevation from end of the
canal to
midlength of the transition should be equal to half of the total drop through the entire length.
From canal end to midlength, the individual drops should be proportional to the square of the distance (a forward parabola).
From midlength to beginning of flume, the drops should mirror those of the first half-length, in reverse order (a backward parabola).
Using this procedure, a smooth curve is obtained for the water-surface profile.
Freeboard. The customary rules for the estimation of freeboard for lined and unlined canals may be used.
For flow depths exceeeding 12 ft (4 m), the freeboard in transitions should be examined carefully.
Energy loss in transitions
For inlet structures, the velocity at the entrance section is less than the velocity at the exit; hence, the water surface must drop
at least the full difference between the velocity heads plus a small conversion loss known as the inlet loss.
Therefore, the drop Δy' in water-surface elevation for an inlet structure is:
Δy' = Δhv + ci Δhv = ( 1 + ci ) Δhv
| (1) |
where Δhv is the velocity head difference between entrance and exit sections.
For outlet structures, the velocity at the entrance section is greater than the velocity at the exit; hence, the water surface must rise
to recover velocity head. The drop is equal to the full difference between the velocity heads minus a small conversion rise known as the outlet rise.
Therefore, the drop Δy' in water-surface elevation for an outlet structure is:
Δy' = Δhv - co Δhv = ( 1 - co ) Δhv
| (2) |
Figure 3 shows the following typical designs: (a) an inlet transition from canal to flume, and (b) an outlet transition from
flume to canal. The step-by-step design of an inlet transition between canal and flume is explained below.
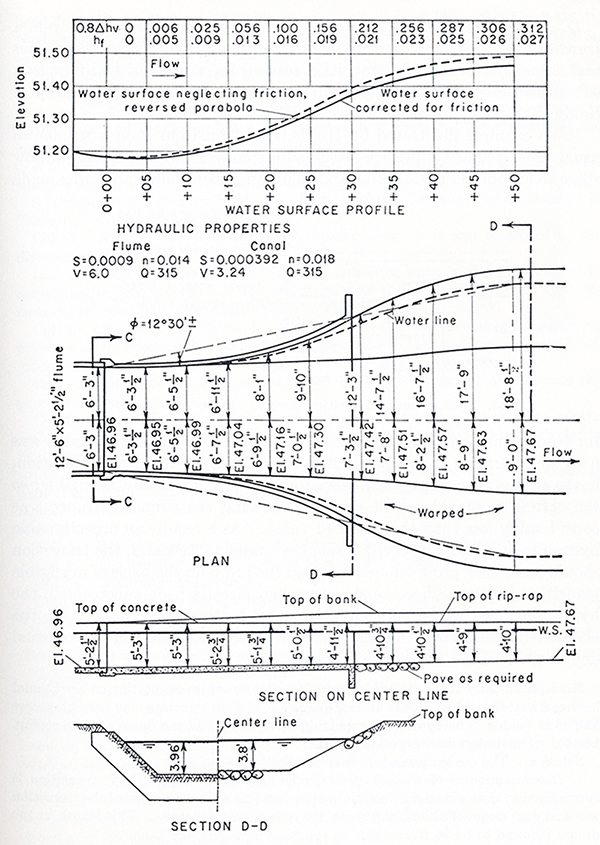
The design of an outlet transition
follows the same general steps as in the case of the inlet transition. However, the outlet transition is often complicated due to the presence of uneven velocity distribution.
In this case, the velocity distribution coefficients may be appreciably greater than one (1) and, therefore, should be considered in the design.
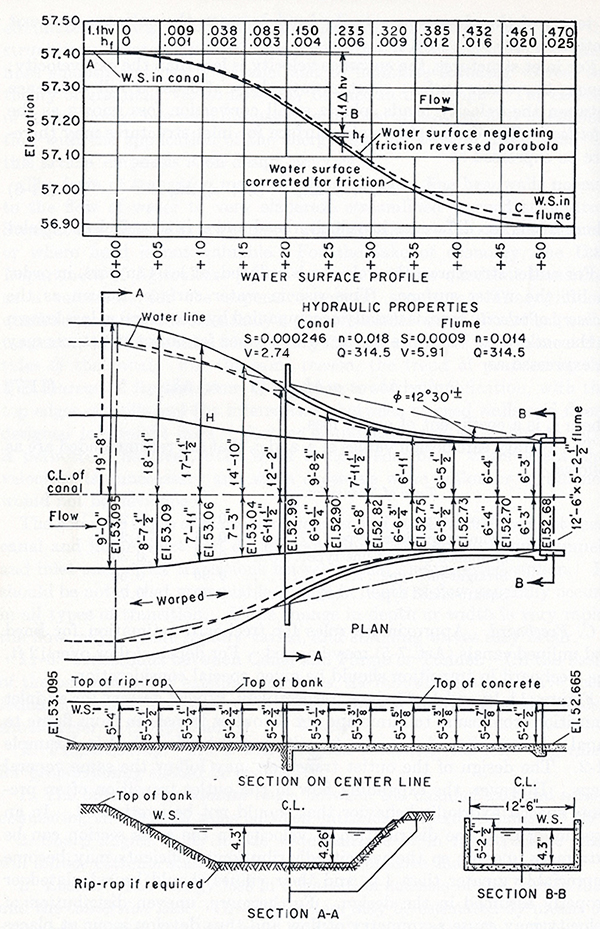
| [Click on figure to display] |
Fig. 3 (a) Design of an inlet transition (Modified from Chow, 1959).
| [Click on figure to display] |
Fig. 3 (b) Design of an outlet transition (Chow, 1959).
Design of an inlet transition: Example
The following example was originally presented by Hinds (1928)
and subsequently cited by Chow (1959).
It is reproduced here with detailed explanation and minor corrections for rounding accuracy. |
Design an inlet transition to connect
an unlined canal of bottom width b = 18 ft and side slope
z = 2 H: 1 V, with a rectangular concrete flume
of width b = 12.5 ft. The hydraulic conditions are:
Design discharge: Q = 314.5 cfs
Canal bottom slope: S = 0.000246
Manning's n of canal: n = 0.018
Flume bottom slope: S = 0.0009
Manning's n of flume: n = 0.014
Water-surface elevation
immediately upstream of the transition, at Station 0 + 00: Zw,0 = 57.410 ft.
Table 2 shows the hydraulic
properties of the canal and flume, corresponding to normal flow: depth yn (ft),
velocity Vn (fps),
flow area An (sq. ft.),
wetted perimeter Pn (ft),
top width Tn (ft),
hydraulic radius Rn (ft), and
hydraulic depth Dn (ft). The hydraulic properties were calculated
using
onlinechannel01.
Table 2 Hydraulic properties of the canal and flume.
|
| Type |
b |
z |
S |
n |
yn |
Vn |
An |
Pn |
Tn |
Rn |
Dn |
| Canal |
18.0 |
2 |
0.000246 |
0.018 |
4.311 |
2.74 |
114.77 |
37.28 |
35.244 |
3.079 |
3.256 |
| Flume |
12.5 |
0 |
0.0009 |
0.014 |
4.254 |
5.914 |
53.18 |
21.008 |
12.5 |
2.531 |
4.254 |
|
Solution Procedure.
-
Length of the transition.
To determine the length of the transition, a straight line
joining the flow line (on the wall) at the two ends of the transition
should make an angle θ = 12.5° with the longitudinal alignment.
The length of the transition is equal to half of the difference between the normal top widths of canal and flume,
divided by tan θ:
L =
0.5 ( Tn canal - Tn flume ) / tan θ
| (3a) |
L =
0.5 (35.244 - 12.5) / 0.2217 = 51.3 ft
| (3b) |
Assume L = 50 ft as a round number to be used for design.
Difference in velocity head.
The velocity head at the upstream cross section (end of canal) is:
hv = (2.74)2 / (2 × 32.17) = 0.117 ft
| (4b) |
Likewise, the velocity head at the downstream cross section (beginning of flume) is: hv = 0.544 ft.
The velocity head difference is:
Δhv =
0.544 - 0.117 = 0.427 ft.
| (5) |
Energy losses, neglecting
friction. For a warped transition,
shown in Fig. 2 (a),
the inlet loss coefficient is ci = 0.1 (Table 1).
Therefore, the total drop in water-surface elevation, neglecting frictional losses, is (Eq. 1):
Δy' =
1.1 × 0.427 = 0.470 ft.
| (6) |
Calculation of drop in water-surface elevation.
The water-surface
elevation (water-surface profile) may be approximated as two equal parabolas, pieced together at midpoint of the transition,
positioned in such a way that the forward parabola is
tangent to the flow at the end of the canal, and the backward parabola is tangent to the flow at the
start of the flume. The two parabolas are tangent to themselves at midpoint of the
transition (Hinds, 1928). The following drops are fixed:
- At the upstream section, Station 0 + 00, the drop is 0.000 ft;
- At midlength, Station 0 + 25, the drop is half the full drop, i.e., 0.235 ft; and
- At the downstream section, Station 0 + 50,
the drop is the full drop: 0.470 ft.
Assume that the length L of the transition is divided into n = 10
equal subreaches, making a total of eleven (11) stations or cross sections, at a distance of 5-ft apart.
To calculate the drops, define a as the half-length of the transition;
thus, a = 25 ft. Furthermore, define b as one-half of the total drop in water-surface elevation Δy'.
Thus, b = 0.235 ft.
For each station i, the forward parabola is defined by varying i from 1 to 5 as follows:
Δy'i =
(b /a 2) xi 2
| (7a) |
For instance, for i = 1:
Δy'1 =
(0.235 / 25 2) 5 2 = 0.0094 ≅ 0.009
| (7b) |
The backward parabola is defined by varing i from 9 to 6 as follows:
Δy'i =
Δy'10 -
Δy'10 - i
| (7c) |
For instance, for i = 9:
Δy'9 =
Δy'10 -
Δy'1 = 0.470 - 0.009 = 0.461
| (7d) |
Similarly, for i = 8:
Δy'8 =
Δy'10 -
Δy'2 = 0.470 - 0.038 = 0.432
| (7e) |
Table 3 shows the partial drop in
water-surface elevation Δy'i corresponding to
each station i, calculated using Eq. 7.
These values are inserted in Col. 2 of Table 4.
Table 3 Calculation of drop in water-surface elevation.
|
| Station |
0+00 |
0+05 |
0+10 |
0+15 |
0+20 |
0+25 |
0+30 |
0+35 |
0+40 |
0+45 |
0+50 |
| i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| xi (ft) |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
| Δy'i (ft) |
0.000 |
0.009 |
0.038 |
0.085 |
0.150 |
0.235 |
0.320 |
0.385 |
0.432 |
0.461 |
0.470 |
|
The computational procedure consists of the following steps, detailed in Table 4 below:
Column 1 shows the eleven (11) stations, from Station 0 + 00 to Station 0 + 50.
Column 2 shows the partial drops in water-surface elevation Δy'.
Column 3 shows the change in velocity head Δhv,
equal to the value of Col. 2 divided by 1.1 (from Eq. 6).
Column 4 shows the velocity heads at each cross section,
beginning with 0.117 ft at the upstream end (Sta. 0 + 00) to 0.544 ft at the downstream end (Sta. 0 + 50).
To calculate the values of Col. 4, for each station, the values of Col. 3 are added to the value for Col. 4, Sta. 0 + 00 (0.117).
Column 5 shows the velocity V corresponding to the velocity head hv of Col. 4:
V = (2 × 32.17 × hv)1/2
| (8b) |
Column 6 shows the flow area A, obtained by dividing the discharge (Q = 314.5 cfs) by the corresponding velocity of Col. 5.
Column 7 shows half the top width 0.5 T,
obtained from the sketched plan [(Fig. 3 (a)].
The plan may be chosen arbitrarily or by trial,
until satisfactory results are obtained (Chow, 1959).
The values shown here are those of the original example (Hinds, 1928).
Column 8 shows half the bottom width 0.5 b, obtained from the cross sections of the sketched plan [(Fig. 3 (a)]. The values shown here are those of the original example (Hinds, 1928).
Column 9 shows the flow depth y, calculated as follows:
y = A / (0.5 T + 0.5 b).
| (9) |
Note that at the downstream end of the
transition, the flow depth for Sta. 0 + 50 has been adjusted
to 4.242 ft.
Column 10 shows the wetted perimeter P, calculated as follows:
P = 2 { 0.5 b + [ ( 0.5 T - 0.5 b )2 + y 2 ] 0.5 }
| (10) |
Column 11 shows the hydraulic radius:
Column 12 shows the friction slope,
calculated using the Manning equation:
V = ( 1.486 / n ) R 2/3 Sf 1/2
| (12) |
Therefore:
Sf = 0.45286 V 2 n 2 R - 4/3
| (13) |
in which n = 0.014 (the flume value) is used for all sections in the transition.
Column 13 shows the incremental friction head loss Δhf between two
adjoining sections, calculated as the equidistance (5 ft) multiplied by the average friction slope for the indicated reach:
Column 14 shows the cumulative friction head loss ∑ Δhf.
| Table 4 (a) Tabular computation for the design of an inlet transition. |
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
(11) |
(12) |
(13) |
(14) |
| Variable |
Δy' |
Δhv |
hv |
V |
A |
0.5 T |
0.5 b |
y |
P |
R |
Sf |
Δhf |
∑ Δhf |
| Station |
(ft) |
(ft) |
(ft) |
(fps) |
(ft2) |
(ft) |
(ft) |
(ft) |
(ft) |
(ft) |
|
(ft) |
(ft) |
| 0 + 00 |
0.000 |
0.000 |
0.117 |
2.740 |
114.771 |
17.600 |
9.000 |
4.315 |
37.243 |
3.082 |
0.000150 |
- |
- |
| 0 + 05 |
0.009 |
0.009 |
0.125 |
2.839 |
110.790 |
17.000 |
8.625 |
4.324 |
36.100 |
3.069 |
0.000160 |
0.000773 |
0.000773 |
| 0 + 10 |
0.038 |
0.034 |
0.151 |
3.116 |
100.947 |
15.427 |
7.917 |
4.324 |
33.166 |
3.044 |
0.000200 |
0.000889 |
0.001662 |
| 0 + 15 |
0.085 |
0.0777 |
0.194 |
3.529 |
89.120 |
13.460 |
7.250 |
4.303 |
29.611 |
3.010 |
0.000250 |
0.001124 |
0.002786 |
| 0 + 20 |
0.150 |
0.137 |
0.253 |
4.037 |
77.900 |
11.228 |
6.958 |
4.284 |
26.013 |
2.995 |
0.000340 |
0.001474 |
0.004260 |
| 0 + 25 |
0.235 |
0.213 |
0.330 |
4.609 |
68.235 |
9.139 |
6.771 |
4.289 |
23.340 |
2.923 |
0.000450 |
0.001966 |
0.006226 |
| 0 + 30 |
0.319 |
0.290 |
0.407 |
5.117 |
61.457 |
7.717 |
6.667 |
4.273 |
22.133 |
2.777 |
0.000600 |
0.002617 |
0.008842 |
| 0 + 35 |
0.385 |
0.350 |
0.467 |
5.480 |
57.387 |
6.847 |
6.563 |
4.279 |
21.704 |
2.644 |
0.000730 |
0.003312 |
0.012154 |
| 0 + 40 |
0.432 |
0.393 |
0.509 |
5.725 |
54.930 |
6.458 |
6.458 |
4.253 |
21.422 |
2.564 |
0.000830 |
0.003895 |
0.016050 |
| 0 + 45 |
0.460 |
0.418 |
0.535 |
5.868 |
53.599 |
6.315 |
6.315 |
4.244 |
21.118 |
2.538 |
0.000880 |
0.004279 |
0.020329 |
| 0 + 50 |
0.470 |
0.427 |
0.544 |
5.914 |
53.177 |
6.250 |
6.250 |
4.254 |
21.008 |
2.531 |
0.000900 |
0.004457 |
0.024786 |
|
Column 15 [Table 4 (b)] shows the water-surface elevation.
At Station 0 + 00: Zw,0 = 57.410 ft.
For each cross section i, the water-surface elevation is:
Zw,i = Zw,0 -
Δy'i - ∑ Δhf,i
| (15) |
Column 16 shows the channel bottom elevation.
For each cross section i, the channel bottom elevation is:
Column 17 shows the side slope z, calculated as follows:
z = (0.5 T - 0.5 b) / y
| (17) |
Column 18 shows the elevation of the top of lining ZL.
To facilitate construction lof the lining, the elevation ZL makes a straight line through the transition.
The recommended height of lining above the water surface for Q = 314.5 cfs is about 1 ft.
Accordingly, the value of ZL at midpoint of the transition (Sta. 0 + 25) should be:
ZL (Sta. 0 + 25) = Zw (Sta. 0 + 25) + 1
| (18a) |
ZL (Sta. 0 + 25) = 57.169 + 1 = 58.169
| (18b) |
The total drop in water-surface elevation
through the transition is [Table 4 (b), Col. 15]:
ΔZw = 57.410 - 56.915 = 0.495
| (19) |
Within any two adjacent cross sections, the drop in water-surface elevation is: 0.495/10 = 0.0495.
Therefore, the elevation of the top of lining upstream of the transition is:
ZL (Sta. 0 + 00) = 58.169 + (5 × 0.0495) = 58.416
| (20) |
Likewise, the elevation of the top of lining downstream of the transition is:
ZL (Sta. 0 + 50) = 58.169 - (5 × 0.0495) = 57.922
| (21) |
The values of ZL for the remaining cross sections are obtained by linear interpolation.
Column 19 shows the height of the lining HL, calculated as follows:
Column 20 shows the computed values of
the half-width 0.5 W, measured at the top of the lining:
0.5 W = z HL + 0.5 b
| (23) |
Column 21 shows the adopted
value of the half-width 0.5 W, measured at the top of the lining.
The values of Col. 21 are indicated in the plan view shown in
Fig. 3 (a).
| Table 4 (b) Tabular computation for the design of an inlet transition (continued). |
| (1) |
(15) |
(16) |
(17) |
(18) |
(19) |
(20) |
(21) |
| Variable |
Zw |
Zb |
z |
ZL |
HL |
0.5 W
(computed) |
0.5 W
(adopted) |
| Station |
(ft) |
(ft) |
z H: 1 V |
(ft) |
(ft) |
(ft) |
(ft-in) |
| 0 + 00 |
57.410 |
53.095 |
1.993 ≅ 2 |
58.416 |
5.321 |
19.605 |
19'-8" |
| 0 + 05 |
57.400 |
53.076 |
1.937 |
58.367 |
5.290 |
18.873 |
18'-11" |
| 0 + 10 |
57.371 |
53.046 |
1.737 |
58.317 |
5.271 |
17.071 |
17'-1.5" |
| 0 + 15 |
57.323 |
53.019 |
1.443 |
58.268 |
5.248 |
14.824 |
14'-10" |
| 0 + 20 |
57.255 |
52.972 |
0.997 |
58.218 |
5.246 |
12.188 |
12'-2" |
| 0 + 25 |
57.169 |
52.880 |
0.552 |
58.169 |
5.289 |
9.691 |
9'-8.5" |
| 0 + 30 |
57.082 |
52.809 |
0.246 |
58.120 |
5.310 |
7.972 |
7'-11.5" |
| 0 + 35 |
57.013 |
52.733 |
0.066 |
58.070 |
5.337 |
6.917 |
6'-11" |
| 0 + 40 |
56.962 |
52.709 |
0 |
58.021 |
5.312 |
6.458 |
6'-5.5" |
| 0 + 45 |
56.929/td>
| 52.686 |
0 |
57.971 |
5.286 |
6.315 |
6'-4" |
| 0 + 50 |
56.916 |
52.661 |
0 |
57.922 |
5.260 |
6.250 |
6'-3" |
|
The design of a channel transition may be performed with the aid of the
onlinetransitiondesign.php
calculator featured in ponce.sdsu.edu.
3. SUMMARY
The hydraulic design of a channel transition is described and explained.
The calculation of an inlet transition between canal and flume is
shown by an example,
originally presented by Hinds (1928)
and subsequently cited by Chow (1959). The example is reproduced
with detailed explanation and minor corrections for rounding accuracy.
An online calculator is provided.
References
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York.
Hinds, J. 1928. The hydraulic design of flume and siphon transitions. Transactions,
American Society of Civil Engineers, Vol. 92, 14-23-1459.
|