El tema de la inestabilidad de la superficie libre en canales abiertos ha interesado a varios investigadores y profesionales, comenzando con Vedernikov (1945), quien desarrolló el criterio que lleva su nombre. El número de Vedernikov V = 1 describe la condición de estabilidad neutra, que separa el flujo estable (V < 1) del inestable (V > 1) (Chow 1959). El flujo estable atenúa las perturbaciones, mientras que el flujo inestable no las atenúa. Por lo tanto, el flujo inestable puede promover el desarrollo de ondas de rollo en canales suficientemente empinados (Ponce y Maisner, 1993). Además, bajo flujos con alto número de Vedemikov, las ondas de inundación pueden empinarse hasta convertirse en ondas de choque cinemáticas (Lighthill y Whitham, 1955; Ponce y Windingland 1985; Porras 1994).

Craya (1952) mejoró el criterio de Vedernikov interpretándolo como la relación entre la celeridad de la onda cinemática relativa y la celeridad de la onda dinámica relativa. Posteriormente, Liggett (1975) desarrolló la ecuación diferencial del canal estable, para el cual V = 0 para todos los números de Froude (F ≤ ∞). Esta condición es demasiado amplia, porque es probable que el máximo número de Froude que se pueda alcanzar en la práctica sea mucho menor que ∞ (generalmente es menos de 20). En su lugar, se puede diseñar un canal estable eligiendo un número de Froude neutralmente estable F_ns que sea mucho menor que ∞, de modo que V ≤ 1 para los números de Froude en el rango F ≤ F_ns. Esta proposición es examinada en este artículo.

La celeridad relativa de la onda cinemática, o la velocidad relativa de Seddon (Seddon 1990), esta dada por la siguiente ecuación:

crk = ( β - 1 ) v

(1)

en la cual v = velocidad media; y β es el exponente de la curva de gasto:

Q = α A β

(2)

en la cual Q = descarga; y A = área de flujo.

La celeridad de onda dinámica relativa de pequeña amplitud, o celeridad de Lagrange (Chow 1959), esta dada por la siguiente ecuación:

crd = ( g D )1/2

(3)

en la cual g = aceleración de la gravedad; y D = profundidad hidráulica, definida como sigue:

A D = ____          T

(4)

en la cual T = ancho superior.

El número de Froude es el siguiente (Chow 1959):

v F = __________        ( g D )1/2

(5)

Utilizando las Ecs. 1, 3 y 5, el número de Vedernikov se puede expresar de la siguiente forma:

V = ( β - 1 ) F

(6)

La Ecuación 6 enfatiza el significado físico de β, o más bien de β - 1, ya que, por definición, la celeridad de la onda cinemática relativa adimensional es la siguiente:

cdrk = β - 1

(7)

La ecuación de Manning en unidades SI es la siguiente (Chow 1959):

1 v = ___ R 2/3 So1/2        n

(8)

en la cual v = velocidad media (v = Q/A); n = coeficiente de rugosidad de Manning; R = radio hidráulico (R = A/P); P = perímetro mojado; y S_o = pendiente de fondo.

Suponiendo una función de forma de la sección transversal P = k A^δ, las Ecs. 2, 7 y 8 conducen a lo siguiente:

2 cdrkM = ____ ( 1 - δ )                3

(9)

en la cual c_drkM = celeridad de la onda cinemática relativa adimensional bajo la fricción de Manning.

La forma de la sección transversal se caracteriza por el parámetro δ, que varía típicamente en el rango 0 ≤ δ ≤ 1. En general, δ varía con la profundidad de flujo, como en el caso de canales rectangulares y trapezoidales. Sin embargo, hay tres casos especiales para los cuales δ es una constante.

Caso 1: El canal hidráulicamente ancho, para el cual δ = 0. En este caso, el perímetro mojado es constante (P = k) e independiente del área de flujo (dP/dA = 0). Esta sección transversal teórica es el límite asintótico de todos los canales anchos (Chow 1959).

Caso 2: El canal triangular, para el cual δ = 1/2. En este caso, dP/dA = (1/2)/R. La forma actual de un canal triangular es una función de la pendiente lateral z (z Horizontal: 1 Vertical).

Caso 3: El canal inherentemente estable, para el cual δ = 1 (Ponce 1991). En este caso, el radio hidráulico es una constante (R = R_o = 1/k) y el perímetro mojado es proporcional al área de flujo: P = k A. Esta sección transversal teórica es el límite asintótico de todos los canales estables.

De estos casos se infiere lo siguiente:

dP δ = R _____             dA

(10)

La definición convencional del número de Vedernikov (Vedernikov 1945; Chow 1959; Jolly y Yevjevich 1970) es la siguiente:

v = x γ F

(11)

en la cual:

1 + b x = ________          2 - b

(12)

en el cual b = exponente del número de Reynolds R en la ley de fricción f = α R^-b; y γ = un factor de forma de la sección transversal, el cual es definido como sigue:

dP γ = 1 - R _____                  dA

(13)

Para la fricción de Manning: b = 1/5, y por lo tanto, x = 2/3. Dadas las Ecs. 7, 9 y 10, se confirma la equivalencia de las dos definiciones del número de Vedemikov (ecuaciones 6 y 11). Además, de las Ecs. 6 y 7, la celeridad de la onda cinemática relativa adimensional se reformula de la siguiente manera:

V cdrk = _____              F

(14)

Para V = 1, F = F_ns, en la cual F_ns es el número de Froude neutralmente estable. Por lo tanto:

Fns = cdrk-1

(15)

Liggett (1975) derivó la ecuación diferencial para el canal estable, definido como aquél para el cual δ es una constante e igual a 1. Aquí extendemos la definición de canal estable a los casos en los que δ es una constante pero es menor que 1. Por lo tanto, se pueden formular dos tipos de canales estables:

Tipo 1. Un canal incondicionalmente estable, para el cual δ = 1 (Liggett 1975). éste es el canal inherentemente estable, que presenta c_drk = 0 y F_ns = ∞, y es absolutamente estable (V = 0) para todos los números de Froude (F ≤ ∞) (Ponce 1991). El radio hidráulico es una constante (R_o).

Tipo 2. Un canal condicionalmente estable, para el cual δ < 1. Este canal presenta c_drk > 0 y F_ns < ∞, y es estable (V ≤ 1) para números de Froude en el rango F ≤ F_ns. El radio hidráulico varía con la profundidad del flujo.

Debido a la simetría habitual de las secciones del canal, es apropiado realizar un análisis utilizando la mitad de una sección transversal. De ahora en adelante, el asterisco (_*) se utiliza como subíndice para referirse a mitades de valores; por ejemplo, T_* es la mitad del ancho superior.

El diferencial del perímetro mojado de la sección transversal estable se define de la siguiente manera:

dP* = (dh 2 + dT*2 )1/2

(16)

en la cual h = profundidad del flujo. Dividiendo entre dh, y dado que dA_* = T_* dh, entonces:

dP*                   dT* T* _______ = [ 1 + (______) 2 ] 1/2         dA*                   d h

(17)

Con la Ecuación 10, la Ec. 17 queda expresada de la siguiente manera:

δ T*                   dT* _______ = [ 1 + (______) 2 ] 1/2      R                     d h

(18)

El canal incondicionalmente estable tiene δ = 1 y radio hidráulico R = R_o. Por lo tanto:

d T*              T* _______ = [ (______) 2 - 1 ] 1/2     d h              Ro

(19)

sujeto a T_* > R_o .

El diseño de un canal estable requiere que el radio hidráulico (R_o) se especifique al inicio. Para lograr esto, la sección transversal real del canal debe estar compuesta por dos subsecciones (Liggett 1975): (1) una subsección inferior de forma rectangular, trapezoidal o triangular, y (2) una subsección superior, de forma estable (ver Fig. 1).

Fig. 1   Secciones de canal estable en función del radio hidráulico inicial Ro y el número de Froude neutralmente estable Fns : (a) ho = 0.5 m, Ro = 0.417 m; (b) ho = 0.75 m, Ro = 0.577 m; (c) ho = 1.0 m, Ro = 0.714 m.

La subsección inferior (de ancho de fondo B, profundidad h_o, y pendiente lateral z) define el radio hidráulico R_o en el cual se basa la subsección superior. El parámetro R_o se define en h = h_o de la siguiente manera:

0.5 (2 B* + zho ) ho Ro = ________________________            B* + ho ( 1 + z 2 ) 1/2

(20)

Además de definir R_o, la subsección inferior sirve para transportar los caudales base. En la práctica, los flujos de alta velocidad pueden ocurrir a profundidades de flujo relativamente pequeñas. Esto debe tenerse en cuenta en el diseño de la subsección inferior.

La ecuación diferencial 19 representa una familia de canales incondicionalmente estables, con parámetro R_o. Un solución particular para T_* = T_*o en h = h_o es la siguiente:

( T* / Ro ) + [( T* / Ro )2 - 1 ] 1/2 h = ho + Ro ln { _____________________________________ }                              ( T*o / Ro ) + [( T*o / Ro )2 - 1 ] 1/2

(21)

que se reduce a la solución de Liggett (1975) para el caso especial de T_*o = R_o como sigue:

T*             T* h = ho + Ro ln { _____ + [( _____ )2 - 1 ]1/2 }                             Ro            Ro

(22)

Dado que la fricción tiene un límite inferior y no puede disminuir de manera realista a cero, se deduce que existe un límite superior para el número de Froude que se puede lograr en la práctica. Por lo tanto, un canal de δ constante puede diseñarse para permanecer estable (V ≤ 1) dentro de un rango de número de Froude F ≤ F_ns, en el cual no es probable que se exceda el F elegido para una condición de diseño dada. Por ejemplo, según Chow (1959), un límite superior práctico para el número de Froude puede ser F = 20. En este caso, los parámetros de sección transversal correspondientes son c_drk = 0.05 y δ = 0.925, de las Ecs. 9 y 15.

La extensión de la Ec. 18 al canal condicionalmente estable, para el cual δ < 1 y R varía con la profundidad del flujo, conduce a lo siguiente:

d T*             δ T* _______ = [ (______) 2 - 1 ] 1/2    d h               R

(23)

sujetos a δ T_* > R.

A diferencia de la Ec. 19, la Ec. 23 no se puede integrar analíticamente. La forma de la subsección superior T_* = f (δ, R_o, R) puede obtenerse por integración numérica, dada una selección de F_ns, c_drkM, δ, y el radio hidráulico inicial R_o (el correspondiente a la profundidad h_o de la subsección inferior).

La integración numérica procede seleccionando primero la forma de la subsección inferior y la profundidad total del canal h_f para incluir las subsecciones inferior y superior. En la subsección inferior, la profundidad del flujo varía en el rango 0 ≤ h ≤ h_o; en la subsección superior varía en el rango h_o ≤ h ≤ h_f.

En el caso de una subsección rectangular inferior, se seleccionan la profundidad de flujo h_o y el ancho medio superior T_*o = B_*. Una elección adecuada de F_ns permite el cálculo de c_drkM  y δ a partir de las Ecs. 9 y 15. Los valores iniciales son h = h_o; A_* = B_* h_o; P_* = B_* + h_o; T_* = T_*o; y R = A_* / P_*. La Ecuación 23 se resuelve de h = h_o a h = h_f en incrementos de Δh. Para una mayor precisión, se elige un Δh muy pequeño, como Δh = 0.0001 m. Los valores de ΔT_*, ΔP_*, ΔA_*, P_*, A_*, y R se calculan en cada incremento, en el cual:

ΔP* = ( Δh 2 + ΔT*2 )1/2

(24)

y

ΔA* = 0.5 ( 2 T* + ΔT* ) Δh

(25)

Los valores de h y T_* se actualizan antes de cada incremento.

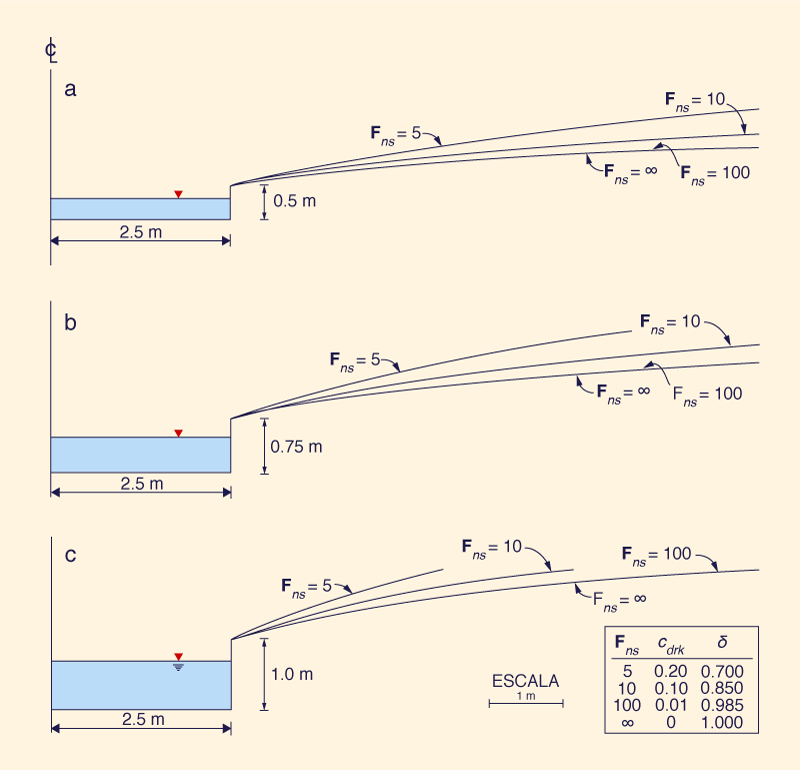
La Figura 1 muestra ejemplos de canales estables calculados utilizando el algoritmo descrito. Las subsecciones inferiores son rectangulares, o de mitad de ancho B_* = 2.5 m. Se muestran tres secciones transversales: Figura 1 (a), h_o = 0.5 m, y R_o = 0.417 m; Fig. 1 (b), h_o = 0.75 m, y R_o = 0.577 m; y Fig. 1 (c), h_o = 1.0 m, y R_o = 0.714 m. Se muestran las secciones transversales estables correspondientes a F_ns = 5, 10, 100, y ∞. Como era de esperar, la sección transversal correspondiente al canal incondicionalmente estable (F_ns = ∞) satisface la Ec. 21.

Las siguientes conclusiones pueden extraerse de la Fig. 1: (1), Para un número de Froude neutralmente estable F_ns, cuanto mayor sea el radio hidráulico inicial R_o, más estrecha será la sección transversal resultante; y (2) Para un radio hidráulico inicial dado R_o, cuanto menor sea la elección de R_o, más estrecha será la sección transversal resultante.

Estos hallazgos tienen importantes implicaciones prácticas. Dada una elección adecuada de R_o y F_ns, se puede diseñar una sección transversal de canal estable relativamente estrecha siguiendo esta metodología. Dicho canal estará en gran parte libre de ondas de rollo y ondas de choque cinemático, siempre que el número de Froude permanezca en el rango F ≤ F_ns.

Se demuestra que el efecto de la forma de la sección transversal sobre la inestabilidad de la superficie libre en el flujo de canales abiertos se caracteriza por la celeridad de la onda cinemática relativa adimensional c_drk = β - 1, en la cual β es el exponente de la curva de gasto caudal-área. Las tres secciones transversales de constante c son: (1) hidráulicamente ancha, con c = 2/3; (2) triangular, con c = 1/3; y (3) inherentemente estable, con c = 0. El valor de c es una función del parámetro de sección transversal δ, el exponente de la relación perímetro mojado-área de flujo (P = k A^δ).

Un canal estable se define como aquél para el cual δ y c_drk son constantes. Se formulan dos tipos de canales estables: (1) incondicionalmente estable, para el cual δ = 1, c_drk = 0 y V = 0 para todos los números de Froude (F ≤ ∞) ; y (2) condicionalmente estable, para el cual δ < 1, c_drk > 0 y V ≤ 1 para números de Froude en el rango F ≤ F_ns, en el que F_ns es el número de Froude neutralmente estable. Se puede diseñar un canal condicionalmente estable seleccionando δ para que coincida con un valor adecuado de F_ns.

Los resultados muestran que cuanto mayor es el radio hidráulico inicial R_o para un F_ns dado, más estrecha es la sección transversal resultante. Asimismo, cuanto menor sea la elección de F_ns para un R_o dado, más estrecha será la sección transversal resultante. Por lo tanto, dada una selección adecuada de R_o y F_ns, se puede diseñar una sección transversal de canal estable relativamente estrecha. Dicho canal estará en gran parte libre de ondas de rollo y ondas de choque cinemático, siempre que el número de Froude permanezca en el rango F ≤ F_ns. Es necesario una investigación adicional para verificar experimentalmente los hallazgos reportados en este artículo.

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill Book Co. Inc,. New York. N.Y.

Craya, A. 1952. "The criterion of the possibility of roll wave formation." Gravity waves, Circular No. 521, National Bureau of Standards, Washington, D. C., 141-151.

Jolly, J. P., y V. Yevjevich. 1970. "Amplification criterion of gradually varied, single peaked waves." Hydro. Paper No. 51, Colorado State University, Fort Collins, Colo.

Ligget, J. A. 1975. "Stability - Chapter 6," Unsteady flow in open channels, Vol 1. K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Fort Collins, Colo., 259-281.

Lighthill, M. J. y G. B. Whitham. 1995. "On kinematic waves I: Flood movement in long rivers.: Proc. Roy. Soc. of London, Vol. A229, London, England, (May), 281-316.

Ponce, V. M. 1991. "New perspective on the Vedernikov number," Water Resour. Res., 27(7), 1777-1779.

Ponce, V. M., y M. P. Maisner. 1993. "Verification of theory of roll wave formation." J. Hydr. Engrg., ASCE, 119(6), 768-773.

Ponce, V. M., y D. Windingland. 1985. "Kinematic shock: Sensitivity analysis," J. Hydr. Engrg., ASCE, 114(4), 600-611.

Porras, P. J. 1994. "Flood wave propagation in inherently stable channels: Theory and applications," MS thesis, Dept. of Civil Engrg., San Diego State University, CA.

Seddon, J. 1900. "River hydraulics," ASCE Trans., Vol. 43, 179-229.

Vedernikov, V. V. 1945. "Conditions at the front of a translation wave disturbing a steady motion of a real fluid," U.S.S.R. Acad. Sciences Comptes Rendus (Doklady), Moskow, U.S.S.R., 48(4), 239-424.