1. INTRODUCCIÓN
Hay dos formulaciones para la difusividad hidráulica en el modelado de ondas de difusión:
2. TEORÍA
Wooding (1965) fue pionero en el uso de ondas cinemáticas con una configuración de "libro abierto" para simular el flujo superficial. Desde entonces, las ondas cinemáticas se han consolidado en la investigación y la prácticas hidrológicas (HEC-1, Flood Hydrograph Package, 1990).
Para hacer frente a esta dificultad, Ponce (1986) ha propuesto un modelo de onda de difusión de flujo superficial basado en el método de Muskingum-Cunge. A diferencia de los modelos de ondas cinemáticas de flujo superficial convencionales, el modelo de ondas de difusión de Muskingum-Cunge tiene la ventaja de que incorpora la difusión física, si la hay, de la escorrentía superficial, combinándola con la difusión numérica del problema en cuestión. Una característica importante de este tipo de modelado es que proporciona independencia de la malla, es decir, los resultados no son una función del tamaño de la malla. Esto libera al usuario del modelo para que se concentre en los aspectos físicos del problema, en lugar de en los numéricos, lo que lleva a un mejor y más consistente modelado.
El modelo de Muskingum-Cunge se basa en la combinación de difusividades físicas y numéricas. La difusividad física es (Hayami, 1951):
La difusividad numérica es (Cunge, 1969):
en la cual c = celeridad de onda, Δx = intervalo de espacio, y X = Factor de ponderación de Muskingum (Chow, 1959). Igualar las difusividades físicas y numéricas conduce a:
y
en la cual
es el número de Reynolds de la celda (Ponce y Yevjevich, 1978).
En el enrutamiento de Muskingum,
en la cual K = tiempo de traslación.
en la cual C = número de Courant (Ponce y Yevjevich, 1978), y Δt = intervalo de tiempo.
Al incluir la inercia en la formulación de las ondas de difusión, Dooge (1973) pudo expresar la difusividad hidráulica en términos del número de Froude:
en la cual v = velocidad media, g = aceleración de la gravedad y d = profundidad hidráulica.
aplicable al caso de fricción de Chezy en canales hidráulicamente anchos.
Dooge et. al. (1982) generalizaron esta formulación para cualquier tipo de fricción y forma de sección transversal:
en la cual β = exponente en la curva de gasto Q = αAβ, con Q = caudal, y A = área de flujo.
El modelo de Dooge es un modelo de ondas de difusión con inercia, que se distingue de un modelo de ondas dinámicas, que implica la solución completa de las ecuaciones gobernantes de continuidad y movimiento (las ecuaciones de Saint Venant). La expresión de Dooge (y Dooge et al.) para la difusividad hidráulica puede considerarse correctamente como una difusividad hidráulica dinámica νd, ya que incluye la inercia en su formulación.
Ponce (1991a, 1991b) mejoró la formulación de Dooge et al. al expresar la difusividad hidráulica dinámica en términos del número de Vedernikov:
El número de Vedernikov [V = (β - 1)F ] es la relación de la celeridad relativa de la onda cinemática crk = (β - 1)ν, a la celeridad relativa de la onda de inercia (celeridad de Lagrange) cri = (gd)1/2 (Craya, 1952). Esto lleva a la definición del número de Reynolds de celda dinámica:
La modificación de Ponce a las expresiones de Hayami y Dooge es importante porque hace que la difusividad hidráulica responda a la dinámica del flujo. En efecto, para el número de Vedernikov
Para aplicaciones de flujo superficial, la pregunta sigue siendo si la difusividad hidráulica dinámica constituye realmente una mejora significativa sobre la difusividad hidráulica cinemática.
3. PROGRAMA EXPERIMENTAL
El trabajo reportado aquí se propuso comparar los resultados del modelo de flujo superficial de ondas de difusión de Muskingum-Cunge usando: (1) el número de Reynolds de la celda cinemática D, Ec. 5; y (2) el número de Reynolds de celda dinámica Dd, Ec. 12. En esencia, se trató de determinar el efecto del número de Vedernikov en la dinámica del flujo superficial bajo una amplia gama de condiciones de flujo (geometría y fricción del fondo, pendientes del plano/canal e intensidad de lluvia efectiva). La comparación se realizó utilizando OVERLAND, un modelo de flujo superficial de ondas de difusión de Muskingum-Cunge desarrollado por el autor principal (Ponce, 1989b). Se implementó una versión especial del modelo para manejar las versiones cinemática o dinámica del número de Reynolds de la celda.
El programa de experimentos numéricos abarcó los tres casos que se muestran en la Tabla 1.
La entrada a OVERLAND es la intensidad de lluvia efectiva ie (cm/h) con una duración especificada tr (hora). El resultado es un hidrograma de salida que muestra el caudal (m3/seg) frente al tiempo (hr). Para cada simulación, la duración de la lluvia se eligió cuidadosamente para permitir que el flujo de salida alcanzara el equilibrio, momento en el cual cesó la lluvia y el flujo retrocedió gradualmente a cero. El caudal en el equilibrio es: Qe = ieA, en el que A = área de captación (Ponce, 1989a). 4. RESULTADOS Los resultados de las simulaciones mostraron un retraso pequeño pero perceptible en la curva ascendente del hidrograma de flujo de salida, junto con un retraso correspondiente en la curva descendente, cuando se compararon las corridas usando números de Reynolds de celdas cinemáticas y dinámicas. La existencia del retraso se atribuye al error de la solución cinemática, que utilizó la formulación original del número de Reynolds de la celda (Ec. 5), en oposición a la solución dinámica, que se basó en la formulación mejorada dependiente del número de Vedernikov (Ec. 12). El error se cuantificó integrando el valor absoluto de la diferencia entre los dos hidrogramas, cinemático y dinámico, para obtener una diferencia de volumen de escorrentía ΔV:
La diferencia de volumen de escorrentía se normalizó dividiéndola por el volumen de escorrentía total Vr = ie trA. Por lo tanto, el error E (en porcentaje) es:
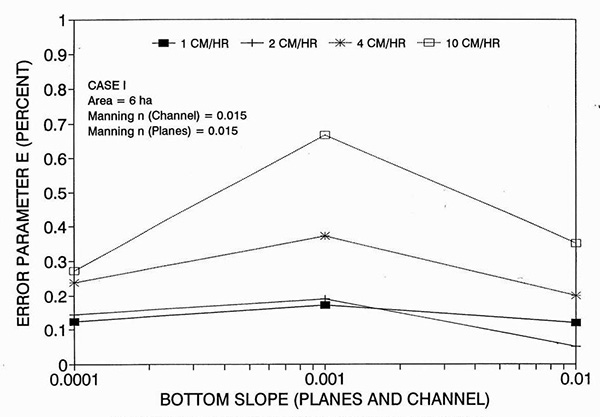
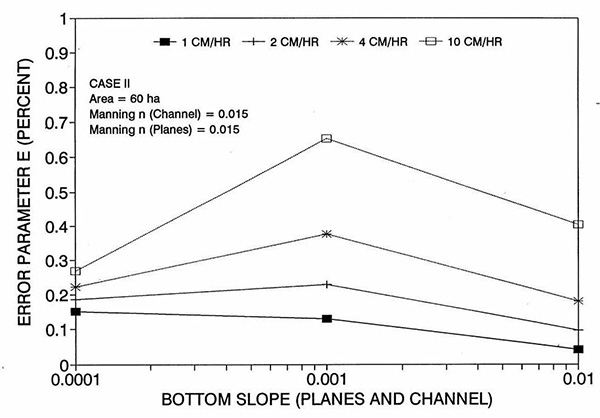
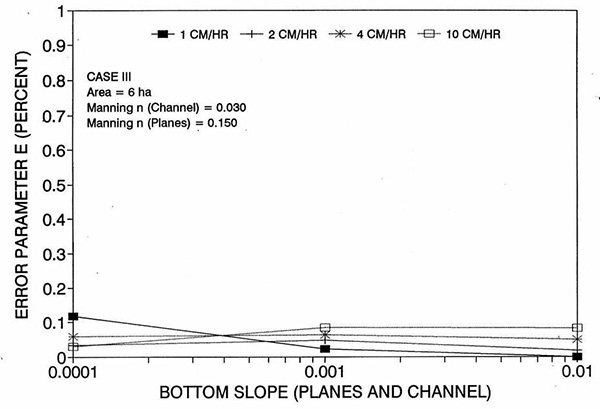
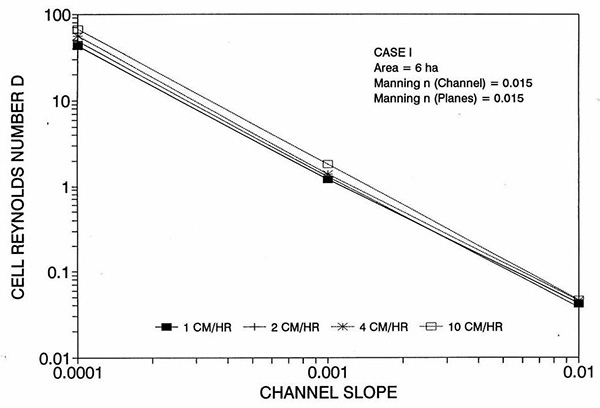
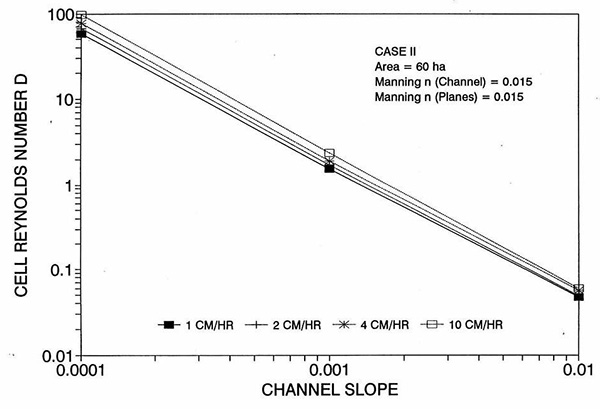
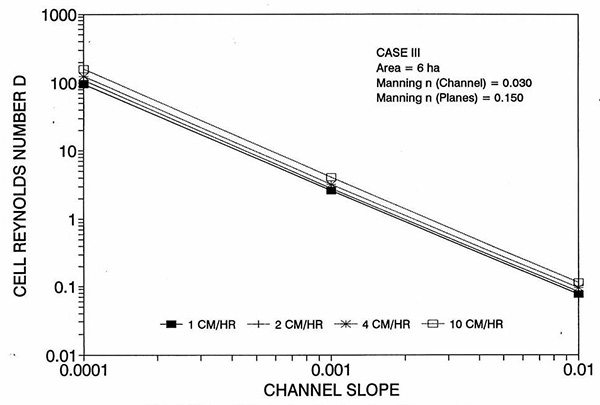
La Figura 1 muestra el error incurrido al usar un número de Reynolds de celda cinemática en una solución de flujo superficial de ondas de difusión, en función de la pendiente del fondo, para cada uno de los tres casos: (a) Caso Ι, (b) Caso ΙΙ, y (c) Caso ΙΙΙ. Estos resultados muestran que el error es realmente pequeño pero perceptible, y es probable que se mantenga dentro del 0.7 por ciento para una amplia gama de condiciones de flujo. Esta figura también muestra que el error está inversamente relacionado con la fricción del fondo: para los Casos I y II, el error es inferior al 0.7 por ciento para intensidades de lluvia inferiores a 10 cm/h; para el Caso ΙΙΙ típicamente es menos del 0.1 por ciento. Los resultados también muestran una tendencia a que el error alcance su punto máximo alrededor del rango medio de las pendientes de fondo (So = 0.001). 5. ANÁLISIS
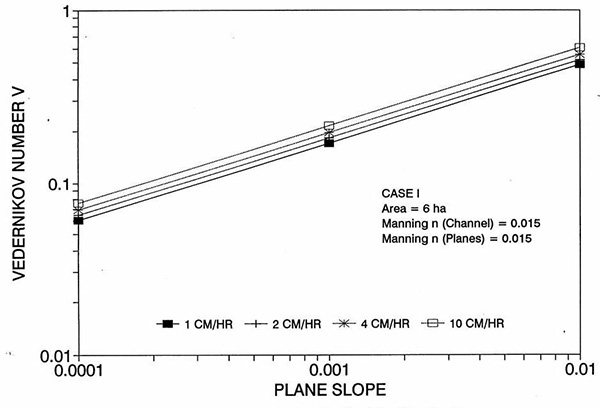
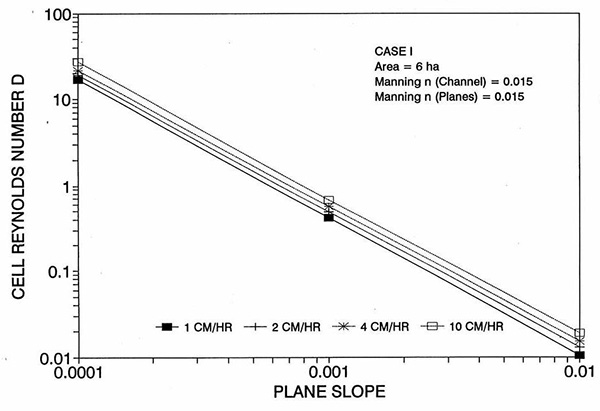
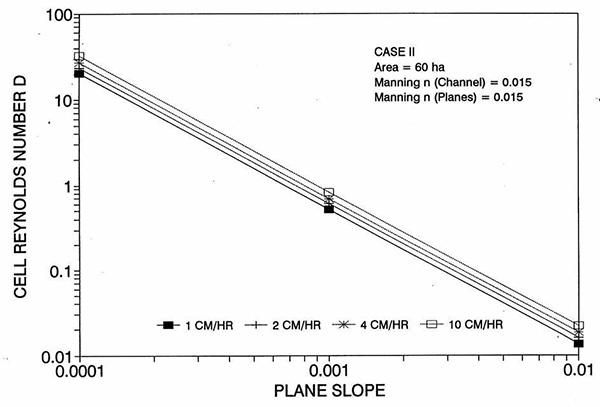
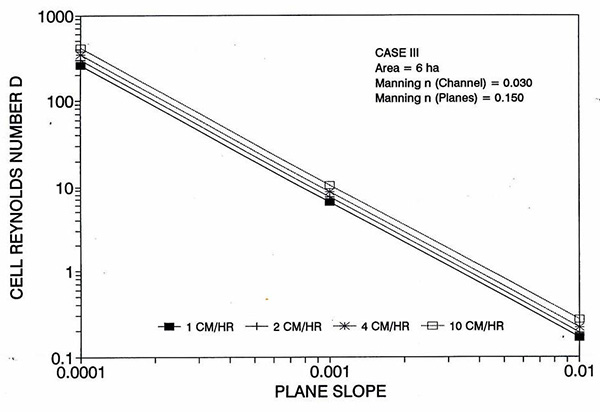
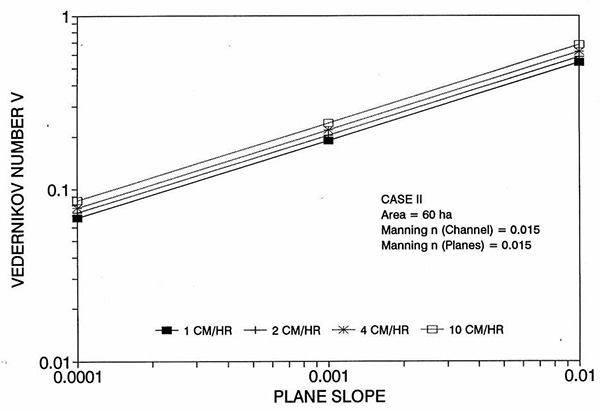
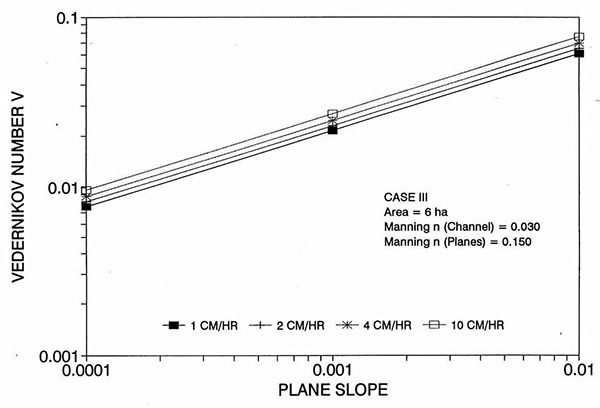
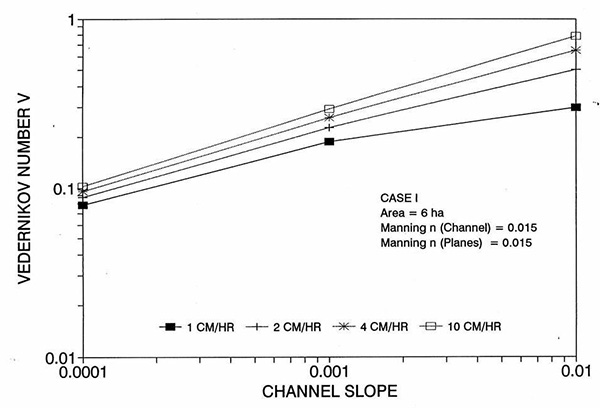
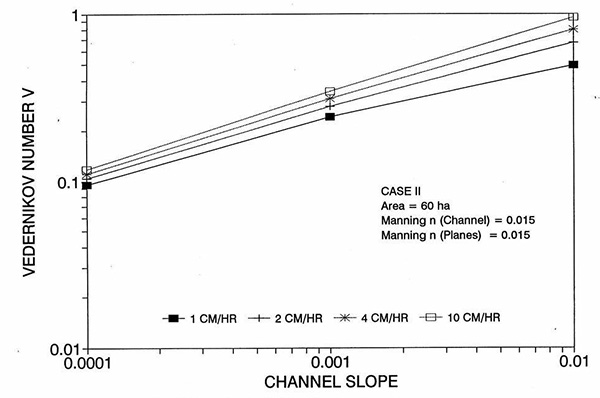
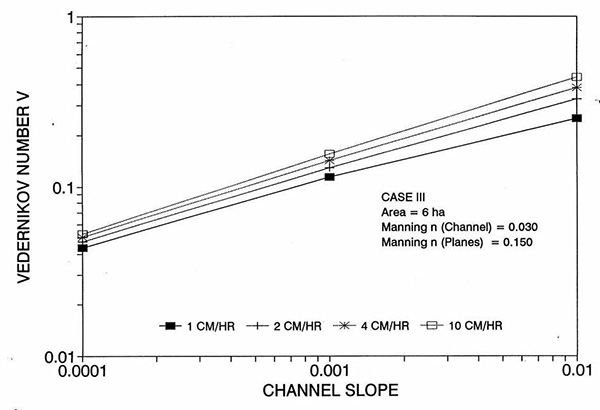
La tendencia del error a alcanzar su punto máximo alrededor del rango medio de las pendientes de fondo requiere más discusión. Las Figuras 2 y 3 muestran la variación del número de Reynolds D de la celda con el plano y la pendiente del canal, respectivamente. Las Figuras 4 y 5 muestran la variación del número V de Vedernikov con el plano y la pendiente del canal, respectivamente.
Estos resultados subrayan la inutilidad de intentar modelar el flujo superficial recurriendo a las ecuaciones hidrodinámicas completas (Chow y Ben-Zvi, 1973; Tayfur et al., 1993). Dado que el modelo de onda de difusión con inercia no mejora sustancialmente la descripción de la dinámica de onda para una amplia gama de condiciones de flujo, se deduce que hay muy poco que ganar si se busca una formulación aún más precisa y elaborada. Además, dado que el modelo de ondas de difusión con inercia no complica indebidamente la formulación, debería ser la forma preferida de modelar el flujo superficial con ondas difusivas. 6. RESUMEN
Se ha realizado un programa de experimentos numéricos para probar el efecto de la difusividad hidráulica dinámica (Dooge, 1973; Ponce, 1991b) frente a la difusividad hidráulica cinemática (Hayami, 1951), cuando se utiliza para modelar el flujo superficial con difusión. Dos modelos
Los resultados mostraron un retraso pequeño pero perceptible en la curva ascendente del hidrograma de flujo de salida, junto con un retraso correspondiente en la curva descendente, al comparar los resultados de los modelos. El retraso se atribuye al error de la solución cinemática, que se basa en el número de Reynolds de la celda cinemática Los hallazgos de este estudio subrayan la inutilidad de intentar modelar el flujo superficial usando las ecuaciones hidrodinámicas completas. Dado que se muestra que el efecto dinámico es pequeño en una amplia gama de pendientes del fondo, un modelo de onda de difusión con inercia puede ser todo lo que se requiere para modelar la dinámica del flujo superficial. Además, dado que el modelo de ondas difusiva con inercia no complica indebidamente la formulación, debería ser la forma preferida de modelar el flujo terrestre utilizando ondas de difusión. BIBLIOGRAFÍA
Chow, V. T., y A. Ben-Zvi. 1973. "Hydrodynamic Modeling of Two-dimensional Watershed Flow." Journal of the Hydraulics Division, ASCE, 99(11), 2023-2040.
Craya, A. 1952. "The Criterion of the Possibility of Roll Wave Formation." Gravity Waves, National Bureau of Standards Circular No. 521, 141-151.
Cunge, J. A. 1969. "On the Subject of a Flood Propagation Computation Method (Muskingum Method)." Journal of Hydraulic Research, 7(2), 205-230.
Dooge, J. C. I. 1973. Linear Theory of Hydrologic Systems. Tech. Bull., No. 1468, USDA Agricultural Research Service, Washington, D.C..
Dooge, J. C. I., W., Strupczewski, and J. J. Napiorkowski. 1982.
"Hydrodynamic Derivation of Storage Parameters in the Muskingum Model." Journal of Hydrology, 54, 371-387.
Hayami, S. 1951. "On the Propagation of Flood Waves." Bulletin Disaster Prevention Research Institute, Kyoto University, 1(1), 1-16.
HEC-1, Flood Hydrograph Package: User's Manual. 1990. U.S. Army Corps of Engineers, Hydrologic Engineering Center, Davis, Calif., September.
Perumal, M. 1992. Comment on "New Perspective on the Vedernikov Number." Water Resources Research, 28(6), 1735.
Ponce, V. M., y D. B. Simons.. 1977. "Shallow Wave Propagation in Open Channel Flow." Journal of the Hydrauclis Division, ASCE, 103(12), 1461-1476.
Ponce, V. M., y V. Yevjevich, V. 1978. "Muskingum-Cunge Method with Variable Parameters." Journal of the Hydraulics Division, ASCE, 104(12), 1663-1667.
Ponce, V. M. 1986. "Diffusion Wave Modeling of Catchment Dynamics." Journal of Hydraulic Engineering, ASCE, 112(8), 716-727.
Ponce, V. M. 1989a. Engineering Hydrology, Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey.
Ponce, V. M. 1989b. "Diffusion Wave Overland Flow Module." Technical Report prepared for USGS Water Resources Division, Stennis Space Center, Miss., June.
Ponce, V. M. 1991a. "The Kinematic Wave Controversy." Journal of Hydraulic Engineering, ASCE, 117(4), 511-525.
Ponce, V. M. 1991b. "New Perspective on the Vedemikov Number." Water Resources Research, 27(7), 1777-1779.
Tayfur, G., M. L. Kavvas, and R. S. Govindaraju. 1993. Applicability of St. Venant Equations for Two-dimensional Overland Flow Over Rough Infiltrating Surfaces. ASCE Journal of Hydraulic Engineering, 119:51-63.
Wooding, R. A. 1965. "A Hydraulic Model for the Catchment-Stream Problem." Journal of Hydrology, 3, 254-267.
SIMBOLOGÍA
A = área de flujo, área de la cuenca;
C = número de Courant;
c = celeridad de la onda;
cri = celeridad relativa de la onda de inercia (celeridad de Lagrange);
crk = celeridad relativa de la onda cinemática;
D = número de Reynolds de la celda cinemática;
Dd = número de Reynolds de la celda dinámica;
d = profundidad hidráulica;
do = profundidad de flujo de referencia;
E = porcentaje de error;
F = número de Froude;
g = aceleración de la gravedad;
ie = intensidad de precipitación efectiva;
K = tiempo de traslación de Muskingum;
L = longitud de la onda;
Lo = longitud del canal de referencia;
n = coeficiente de rugosidad de Manning;
Q = caudal;
Qe = caudal de equilibrio;
qo = caudal unitario de referencia;
So = pendiente de fondo;
t = variable tiempo;
tr = duración de la precipitación efectiva;
V = número de Vedernikkov;
Vr = volumen total de escorrentía;
v = velocidad media;
X = factor de ponderación de Muskingum;
α = coeficiente de la curva de gasto Q = αAβ;
β = exponente de la curva de gasto Q = αAβ;
Δt = intervalo de tiempo;
Δx = intervalo de espacio;
ΔV = diferencia de volumen de escorrentía;
ν = difusividad hidráulica;
νd = difusividad hidráulica dinámica ;
νk = difusividad hidráulica cinemática ; y
σ = número de onda adimensional.
|
| 220906 10:50 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |