1. INTRODUCTION Dams provide many benefits to society. However, floods caused by dam failures have produced some of the most devastating disasters of the last two centuries [20]. As a result, earth dam failure has become a subject of increasing concern among dam engineers, federal, state, and local officials, and society at large.
There is ample documentation on dam breaches, and the prevailing mechanisms are well understood. However, the causal relationships are not as clear. Studies have shown that earth dam failures can be due to many causes. Generally, these are classified as follows: (a) hydrologic, or Failure usually results in the eventual development of a breach compromising a certain length of the embankment. The breach width has been documented in a large number of cases. Dam breach studies have shown that the shape and time evolution of the breach determines to a large extent the characteristics of the outflow hydrograph [12]. The objective of this paper is to develop a dimensionless relationship between geometric and hydraulic parameters governing earth dam breach failure. For this purpose, the following geometric and hydraulic parameters are defined:
2. CASE STUDIES OF DAM BREACH FAILURES Valuable information is available from documented dam breach failures. Wahl [2] has identified many breach prediction equations. These equations have been based on analyses of case studies comprising from 20-60 failures. Sources of case study data for breached dams are numerous, e.g., Ponce [12], Singh [17], and Wahl [2]. Many of the failures took place before the need was recognised to fully document the breach process and associated breach charateristics. Babb and Mermel [1] summarised over 600 dam incidents throughout the world. However, high quality, detailed information was lacking in most cases. During the 1980s, several researchers compiled databases of well-documented case studies in efforts to develop predictive relations for breach peak outflows [3, 5, 6, 7, 10, 12, 14, 16, 18]. Wahl [20] performed a literature search to produce a single database containing all case studies cited, comprising a total of 108 embankment failures. The type, amount and quality of data available for individual case studies varied widely. There are many instances of significant discrepancies between similar data reported by different investigators. Researchers have proposed many relations for estimating breach parameters and peak outflows. The effect of breach parameters on peak discharge and evacuation time has been reported in the literature. The peak discharge was examined by Singh and Snorrason [15]. Petrascheck and Sydler [11] demonstrated the sensitivity of peak outflow, inundation level, and flood arrival time to changes in breach width and formation time. The shape and time evolution of the breach, along with the size of the dam and reservoir, determine to a large extent the characteristics of the outflow hydrograph during an earth dam breach. Singh and Snorrason [14] provided the first quantitative guidance on breach width when they plotted breach width vs dam height for twenty dam failures. MacDonald and Langridge-Monopolis [10] related the breach time-to-failure to the volume of eroded material. The volume of eroded material was related to the breach formation factor, defined as the product of the outflow volume times the initial depth of water above the breach bottom. Froehlich [5] developed non-dimensional prediction equations for estimating average breach width, average side slope factor, and breach formation time. Froehlich's predictions were based on the characteristics of the dam, including reservoir volume, depth of water above the breach bottom, reach depth, length of embankment at the dam crest, breach bottom width, and empirical coefficients that account for overtopping vs non-overtopping failures and the presence or absence of a core wall. Singh and Snorrason [14,15] presented relations for peak outflow as a function of dam height and reservoir storage.
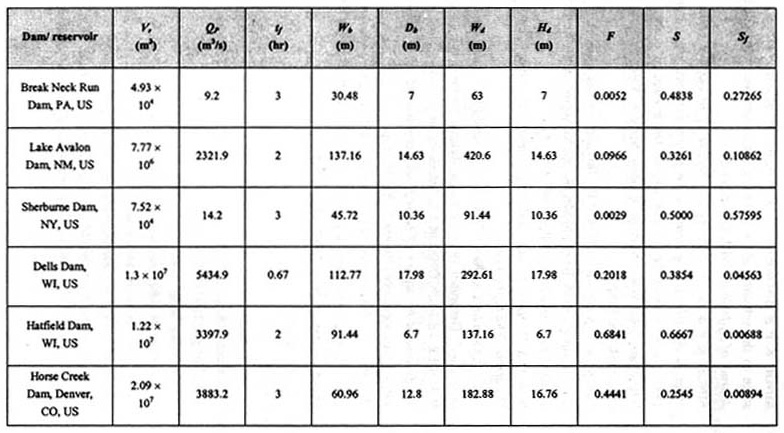
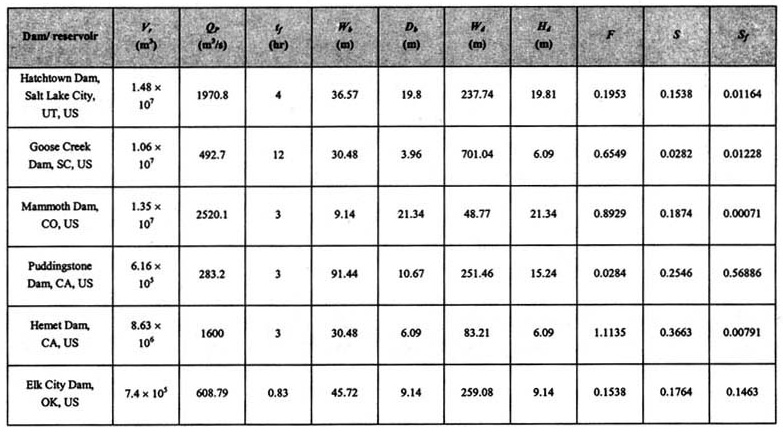
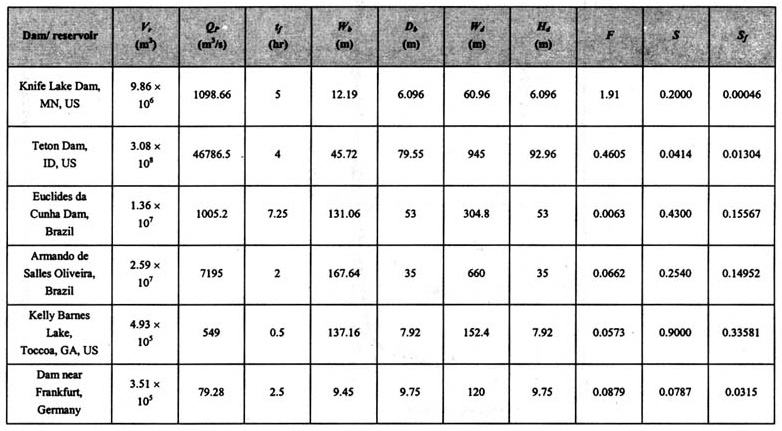
Froehlich [6] developed a regression equation for the prediction of peak outflow based on reservoir volume and hydraulic head. He used data from 22 case studies for which peak outflows were available. Harris and Wagner [8] applied the Schoklitsch sediment transport equation to dam breach outflows. Lou [9] and Ponce and Tsivoglou [13] developed a model that linked the Meyer-Peter and Muller sediment transport equation to the Walder and O'Connor [19] presented a physically-based model of dam breach formation, and used it to relate dimensionless peak outflow to a dimensionless parameter containing a drop in reservoir level, volume of released water, and mean vertical erosion rate of the breach. Fread [4] used a parametric approach to find the dam breach outflow hydrograph, using empirical observations of dam failures. He used hydraulic principles for the prediction of dam breach outflow. Ponce [12] defined a Froude number based on breach peak outflow and related it to a shape factor defined as follows: S = (WbDb) / (WdHd) The result showed a definite trend to an inverse relationship. Ponce's results were very similar to those reported by Black [2]. However, both relations show a poor fit to the data, as depicted in Figure 1.
3. DATA ANALYSIS A comparison was made between Ponce's data and the Dam Safety Office database [20]. It was determined that only 24 cases reported by Wahl [2] are useful for this study. Ostensibly, these are the same as those reported by Ponce [12]. A review of Ponce's work indicates that it was collected directly from original sources. For this reason, it is preferred for use in this study. For completeness, Ponce's data is shown in Table 1.
The following peak outflow Froude number was used in this study:
where g = gravitational acceleration. A new shape factor Sƒ is defined as follows:
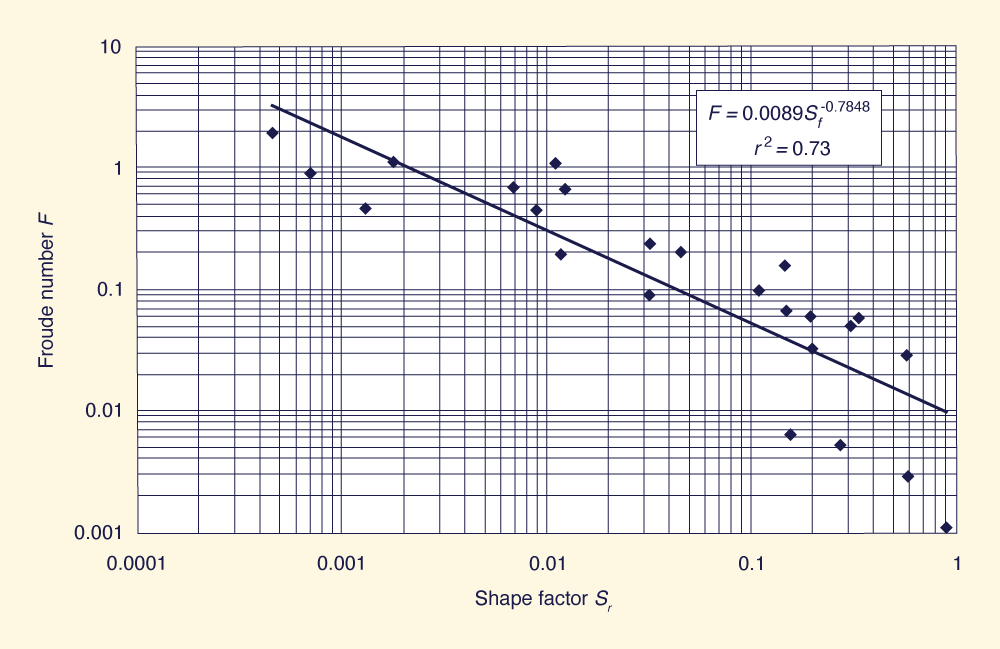
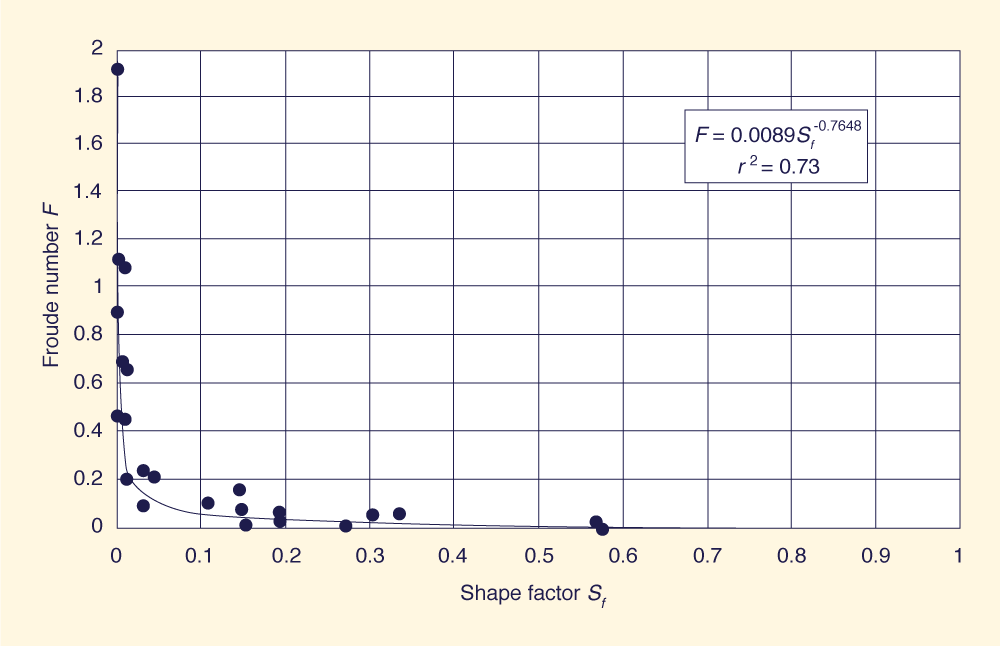
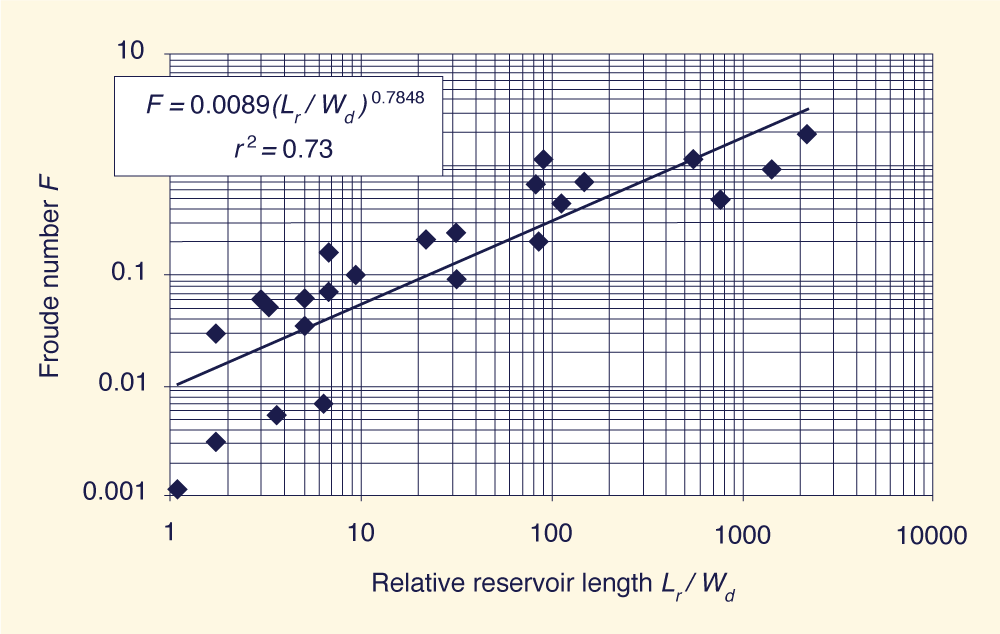
An analysis of the relationship between peak outflow Froude number and the new shape factor Sƒ, based on all the available data, led to the graphs shown in Figure 2 and Figure 3. The relationship is:
with a coefficient of determination r 2 = 0.73.
According to Figure 3, there are two limiting trends:
4. CONCLUSIONS Based on the available data, there appears to be a good correlation between the peak outflow Froude number F and the new shape factor Sƒ. In additiion, the reservoir characteristic length Lr is an indicator of the quantity of water that is responsible for the magnitude of peak outflows during a dam breach. In other words, when Lr increases and/or Wr decrease, F (the Froude number) also increases. REFERENCES
BABB, A. O. and T. W. MERMEL. 1968. "Catalog of dam disasters, failures and accidents", Bureau of Reclamation, Washington, DC, US.
BLACK, E. B. 1925. "Partial failure of earth dam at Horton, Kansas", Engineering News Record, 1925, 95(2), pp58-60.
COSTA, J. E. 1985. "Flood from dam failures", U.S. Geological Survey Open-file Report 85-560, Denver, CO, US, 54p.
FREAD, D. L. 1988. "Breach: an erosion model for earthen dam failures", 1988, NWS Report, National Oceanic & Atmospheric Administration, Silver Spring, MD, US, (revised 1991).
FROEHLICH, D. C. 1987. "Embankment dam breach parameters", Proceedings of the ASCE National Conference on Hydraulic Engineering, 3-7 August,, Williamsburg, VA, US, pp570-575.
FROEHLICH, D. C. 1995. "Peak outflow from breached embankment dam", Proceedings of the ASCE Conference on Water Resources Engineering, 14-18 August 1995(a), San Antonio, TX, US, pp887-89I.
FROEHLICH, D. C. 1995. "Embankment dam breach parameters revisited", Journal of Water Resources Planning & Management, 121(1), pp90-97.
HARRIS, G. W., and WAGNER, D. A. 1967. "Outflow from breached earth dams", 1967, University of Utah, Salt Lake City, UT, US.
LOU, W. C, 1981. "Mathematical modelling of earth dam breaches", Thesis, 1981, presented to Colorado State University, Fort Collins, CO, US (in partial fulfilment of requirements for the Degree of Doctor of Philosophy).
MACDONALD, T. C., and J. L. MONOPOLIS. 1984. "Breaching characteristics of dam failures", Journal of Hydraulic Engineering, 110 (5), pp567-586.
PETRASCHECK, A. W., and P. A. SYDLER. 1984. "Routing of dam break flood", International Water Power & Dam Construction, 36, pp29-32.
PONCE, V. M. 1982. "Documented cases of earth dam breaches", 1982, San Diego State University, SDSU Civil Engineering Series,
PONCE, V. M., and A. J. TSIVOGLOU. 1981. "Modelling gradual dam breaches", Journal of the Hydraulics Division, ASCE, 107(7), pp829-838.
SINGH, K. P., and A. SNORRASON. 1982. "Sensitivity of outflow peaks and flood stage to the selection of dam breach parameters and simulation models", Journal of Hydrology, 68, 295-310.
SINGH, K. P. and A. SNORRASON. 1984. "Sensitivity of outflow peaks and flood stage to the selection of dam breach parameters and simulation models", SWS Contract Report 288, Illinois Department of Energy & Natural Resources, State Water Survey Division, Surface Water Section, University of Illinois, US, 179p.
SINGH, K. P., and P. D. SCARLATOS. 1985. "Breach erosion of earthfill dams and flood routing", BEED Model, Research Report, Army Research Office, Battelle, Research Triangle Park, NC, US, 131 p.
SINGH, V. P. 1996. "Dam breach modelling technology", Kluwer Publisher, Dordrecht, The Netherlands.
SOIL CONSERVATION SERVICE. 1981. "Simplified dam breach routing procedure", December,
Technical Release No 66 (Rev. I), 39p.
WADLER, J. S. and J. E. O'CONNOR. 1997. "Methods for predicting peak discharge of floods caused by failure of natural and constructed earth dams", October, Water Resources Research, 33(10), 12p.
WAHL, T. L. 1998. "Prediction of embankment dam breach parameters", DSO-98-004, Dam Safety Research Report, US Department of the Interior, Bureau of Reclamation, Dam Safety Office.
|
| 240206 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |