1. INTRODUCTION
The kinematic shock is perhaps one of the most elusive topics in unsteady open-channel flow hydraulics. The current physical explanation is that flood waves have an intrinsic nonlinear tendency to steepen as they propagate downstream, eventually leading to shock development.
This apparent pervasiveness of the kinematic shock in the computational laboratory lacks a parallel in the real world. It is widely recognized that only under very unusual circumstances is the kinematic shock likely to develop in actual practice. Furthermore, well documented instances of sightings are almost nonexistent.
This dichotomy between reality and simulation must be traceable to one or several of nature's features not being properly resolved at the chosen level of abstraction. Mathematical models are perforce simplifications of reality, and computer models of unsteady free surface flow phenomena are no exception. For instance, nonlinear flood routing in rectangular prismatic channels sometimes leads to shock development if the computation is carried long enough in both time and space. Normally, such long channels of such cross-sectional uniformity would not occur in nature.
The factors contributing to kinematic shock development are by no means well understood.
2. BACKGROUND
One of the earliest detailed accounts of kinematic shock is that of Lighthill and Whitham (5).
Lighthill and Whitham correctly identified the potential for steepening of the rising limb of the kinematic wave and likened the end product to the observed shocks in gas dynamics; thus, the terms "kinematic shock" and "kinematic shock wave." However, the similarities would appear to end there, because the kinematic shock occurs ostensibly in the absence of inertia. Lighthill and Whitham circumvented this theoretical difficulty by suggesting that the shock thickness was indeed finite and of the same order of magnitude as the reference channel length, Lo (6), defined as follows:
in which do = reference flow depth; and So = channel bed slope.
In the almost three decades that have elapsed since the publication of Lighthill and Whitham's classical work, the kinematic shock has continued to play an important role in certain applications of unsteady open-channel flow hydraulics and hydrology. In the field of watershed modeling, the tracking of kinematic shock waves is but a logical consequence of the routing of kinematic waves. Early detailed accounts of numerical calculations of kinematic shocks are given by Kibler and Woolhiser (4) and Harley et al (3). Kibler and Woolhiser (4) looked at the kinematic cascade as a possible hydrologic model and studied the shock-producing properties of several such geometric configurations. By applying the method of characteristics to a cascade of planes, they were able to derive a shock parameter, Ps, as a function of geometric and frictional characteristics of two adjacent planes. According to Kibler and Woolhiser (4), when Ps exceeds unity, shock formation will occur on the downstream plane under spatially uniform distribution of rainfall excess.
"While the shock wave phenomenon may arise under certain highly selective physical circumstances, it is looked upon in this study as a property of the mathematical equations used to explore the overland flow problem rather than an observable feature of this hydrodynamic process."
Harley et al. (3) effectively incorporated the tracking of shock waves into their catchment model based on the method of characteristics. They treated shock waves as minor disturbances in the regular flow field, and simulated normal characteristics and shock fronts on an equal basis.
More recently, Borah et al. (1) have presented an analytical solution to the kinematic wave approximation for unsteady flow routing. The model allows time-dependent lateral inflow with piecewise spatial uniformity and is designed for use in watershed flow simulation. A significant feature of the Borah et al. model is its explicit capability for routing discontinuities that may develop during the course of the computation. A solution based on the method of characteristics and an approximate shock-fitting scheme preserves the effect of the shocks, and enables the routing of a variety of unsteady flows, ranging from simple cascades to complex natural watersheds.
Other references to the calculation of shocks, kinematic or otherwise, are scattered throughout the literature. For instance, Smith (11) developed a method for predicting the rate of movement and attenuation of kinematic flow over an infiltrating plane. Using a numerical procedure, he was able to document certain shock-type features of flood wave movement under specified initial and boundary conditions. Earlier, Tinney and Bassett (12) had reported on analytical and experimental work to predict the terminal shape of a shallow liquid front. For the turbulent flow case, their findings confirm the importance of the reference channel length, Lo (Eq. 1), in dimensionless studies of unsteady open-channel flow phenomena.
Although the concept of kinematic shock is well established in the field of watershed modeling, its transposition to streamflow routing remains a subject of controversy. A few investigators, most notably Cunge (2), have gone as far as to question its existence altogether. There is no doubt that the steepening tendency is real. Whether the unsteady gradually varied flow equations can continue to describe the phenomena in the vicinity of the shock remains to be determined. On more practical grounds, it would be of interest to determine the flow and channel characteristics that will tend either to promote or to inhibit the development of kinematic shock. Such a line of inquiry is pursued in this paper.
3. METHODOLOGY
The approach used herein to study the potential for kinematic shock development consists of the following: (1) Identification of the relevant flow and channel parameters; (2) selection of parameter ranges; (3) selection of a physically based flow routing model; and (4) development of a strategy for testing the sensitivity of the chosen parameters to kinematic shock development under a wide range of conditions.
Parameter Identification. In unsteady open channel flow theory, two parameters characterize linear wave movement in wide channels (6): (1) the reference flow Froude number,
in which Qt = inflow at time t; Qb = baseflow; Qp = peak inflow; tp = time-to-peak of inflow hydrograph; tg = time-to-center-of-gravity of inflow hydrograph; and r = tp / (tg - tp).
Given the aforementioned, the ratio of base-to-peak inflow, Qb / Qp, was chosen as an indicator of relative wave height, and the time-to-peak tp was chosen to depict overall hydrograph time scale.
With regards to the cross-sectional shape parameters, the ones chosen here are those normally used in kinematic wave routing applications: the coefficient α and exponent β in the power fit to the single-valued discharge-flow area relation:
in which Q = discharge; and A = flow area, based on a suitable uniform flow formula (such as Manning's or Chézy's).
Parameter Ranges. The testing program was designed to vary the chosen parameters within suitable ranges. To account for the Froude number variation, a matrix of five bed slopes, So , and five values of Manning's n was established, leading to a framework of 25 channels, each with a unique set of So and n. Adopted values of So , were: 0.01, 0.004, 0.001, 0.0004, and 0.0001; values of n were: 0.01, 0.02, 0.04, 0.08, and 0.10. Mild bed slopes with large Manning's n led to low Froude number flows, while steep bed slopes with small Manning's n resulted in high (even larger than unity) Froude number flows.
In nonlinear flood waves, the steepening of the rising limb tends to be counteracted by the diffusive effects brought upon by the dynamic components. As shown by Ponce and Simons (6), the dimensionless wave number, σ, is an indicator of the relative size of the dynamic components. Accordingly, in order to guarantee a sufficient amount of wave steepening, unimpaired by the dynamic effect, the tested waves were chosen to remain within the realm of kinematic and diffusion waves (generally, low σ values). For this purpose, the time-to-peak, tp of the inflow hydrograph, an indicator of overall time wale, was used to test the satisfaction of the diffusion wave criterion developed by Ponce et al. (7) and subsequently modified (10) for application to gamma hydrographs:
in which N = dimensionless number; g = gravitational acceleration; and all other variables are as previously defined. For each specified flow condition, the satisfaction of Eq. 4 guarantees that the tested wave is properly a kinematic/diffusion wave, and therefore, largely free of very strong diffusive effects that would tend to counteract the development of kinematic shock.
Fig. 1. Rectangular/trapezoidal/triangular cross sections used in this study
The effect of relative wave height was accounted for by varying the ratio of base-to-peak flow.
A complete accounting of the variation of cross-sectional shape parameters, α and β, was deemed too ambitious. A limited yet meaningful program was devised by selecting a family of rectangular/trapezoidal/ hiangular cross sections, using three bottom widths and three side slopes (Fig. I). The bottom widths chosen were B = 0, 10, and 100 m; the side slopes were z = 0, 1, and 10 (0 = horizontal: 1 = vertical). This led to eight channels (the case of B = 0 and z = 0 being trivial) encompassing a wide range of cross-sectional shape parameters. In general, the β value is allowed to vary from the theoretical (Manning friction) β = 1.667 for wide channels of rectangular cross-sectional shape (B = 100 and z = 0), to β = 1.333 for triangular-shaped channels (B = 0 and z = 1). The exception is the case of narrow, rectangular channels (B = 10, z = 0) coupled with low Froude numbers flows (large flow depths) for which the β value approaches 1. The above eight channels were considered to provide a sufficiently wide range of β to allow meaningful conclusions to be drawn from the sensitivity analysis. Model Selection. The SYS75 model was selected as the numerical model to carry out the present study. This model is a computer program developed by the senior writer featuring a physically based coeffident routing module in which the routing parameters are allowed to vary in time and space (8). This gives it the capability for routing nonlinear flood waves, and therefore, the ability to study the wave steepening caused by the nonlinearity. The computer model can calculate discharge, flow area, and stage discretely in space and time, when presented with ap-propriate initial and boundary conditions. The accuracy of the SYS75 model has been extensively documented (10), and it is considered to be adequate for the routing of kinematic and diffusion waves. Additional details on the SYS75 model are given elsewhere (10).
Study Strategy. The overall strategy for accomplishing the study objectives consists of the following: (1) establishing a standardized channel length based on total inflow volume and peak flow area above base flow, to enable shocks to be analyzed at comparable stages of development; In addition, other manifestations of the shock presence such as numerical instabilities are documented as part of the study.
4. TESTING PROGRAM
Seven channels, each with a unique set of bed slope, So and Manning's n, were selected as part of this study. For identification purposes, they were given alphabetic names from A-G, followed by an L or H, depicting either low or high base-to-peak inflow ratio. Channel F was tested under both L and H conditions, and channel G was tested under three different tp ratios, for a total of ten series
For each series, the total channel length is standardized with respect to the inflow volume.
in which m = tp (tg - tp) is an integer. The channel length, Lc is estimated by the following formula (10):
in which Apr = flow area corresponding to Qpr = Qs - Qb. Equation 6 guarantees that the routing length Lc is related to the inflow hydrograph volume, and therefore, remains physically meaningful for kinematic shock comparative studies.
Inflow hydrograph and channel characteristics for the ten series tested herein are given in Table 2.
5. RESULTS
Results for all eighty (80) runs are summarized in Tables 3 and 4. For the sake of clarity, all runs are hereafter referred to by their row and column identification shown in these tables. For instance, run 34 would correspond to row 3 (channel with B = 10 and z = 0) and column 4 (EH series).
Table 3 shows rating curve parameters α and β for all runs. The value of α accounts largely for channel bed slope and bottom friction, and to a lesser extent for the effect of wetted perimeter on cross-sectional shape. The value of β accounts for cross-sectional shape and the type of bottom friction (whether Manning or Chézy). Values of α vary from α = 0.008 (run 64) to α = 5.000 (run 13); values of β varies from β = 1.025 (run 34) to β = 1.664 (run 60). Table 3 shows that β varies generally from the theoretical β = 1.333 for triangular channels (β = 0) with Manning friction, to values close to the theoretical (β = 1.667 for wide rectangular channels (β = 100 and z = 0) with Manning friction. Values of β outside the above range are calculated for narrow channels with relatively large flow depths (low Froude number flows); see for instance, values of β for runs 34 and 37.
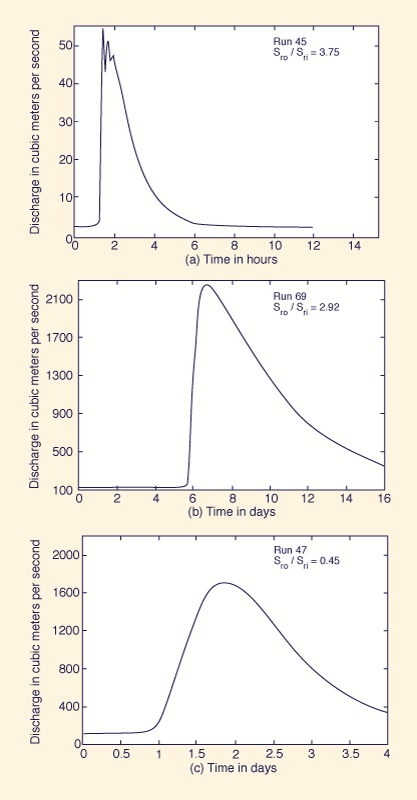
Table 4 shows final slope to initial slope ratios Sro / Sri for all 80 runs. These are ratios of slopes of the rising limb of outflow and inflow hydrographs, respectively. Therefore, the higher the ratio, the more marked the tendency for shock development within the standardized channel length.
All parameters have a definite effect on shock development. The slope ratio, Sro / Sri, is directly proportional to the peak inflow Froude number (channel friction and bed slope), time-to-peak tp, (overall wave time scale), and β value (cross-sectional shape, and to a lesser extent, type of channel friction); and inversely proportional to the ratio Qb / Qp (relative wave height).
The time scale (and therefore, length scale) of the wave is directly related to wave steepening, as shown by the results of channels GL, GL1, and GL2. As tp increases from GL to GL1 and GL2, the wave becomes more kinematic and therefore, more prone to shock development (see for instance, column 9 as compared to column 8). The exception to this pattern is given by runs 37-39, confirming the odd behavior of this particularly narrow channel with a β value near 1. Values of the slope ratio less than 1 (see column 7) indicate wave diffusion instead of wave steepening, signaling the complete absence of the shock.
The Froude number has a definite effect on wave steepening, as shown by comparing results of columns 5 (channel FL, Froude number = 0.7) and 9 (channel CL2, Froude number = 0.1) having the same Qb /Qp, ratio (Qb = 0.05) and approximately the same N value (see Eq. 4). For instance, run 85 shows a slope ratio of 6.0, as compared with 2.79 for run 89.
Cross-sectional shape as embodied in the β value has also a definite influence on wave steepening. Wide channels (rows 6-8) having β values approaching 1.667 show a much stronger tendency for wave steepening than either triangular (rows 1 and 2, β = 1.333) or narrow (rows 3-5, β generally between 1.333 and 1.667). The exception, runs 37-39, show very strong wave diffusion due to their low β value (β = 1.04).
The ratio of base-to-peak inflow, Qb / Qp has a definite effect on wave steepening, m shown by the results of columns 5 and 6, Table 4. The L flow condition consistency produced a larger slope ratio than the H flow condition (see for instance run 75, having a slope ratio of 5.0, as compared to run 76, with a slope ratio of 2.0).
Figure 2 shows typical outflow hydrographs: run 45, showing marked steepening and associated numerical instability
6. SUMMARY AND CONCLUSIONS
A series of numerical experiments has been performed to determine the flow and channel characteristics that are most conducive to kinematic wave steepening and associated kinematic shock phenomena. Relevant flow and channel characteristics are identified at the outset, and a program of 80 computer runs is completed, varying the inflow hydrograph peak Froude number, time-to-peak, base-to-peak flow ratio, and the channel cross-sectional shape. Standardized channel lengths are calculated to enable the analysis of shocks at comparable stages of development. Gamma hydrograph inflows are routed from upstream to downstream using a physically based flow routing computer model.
It is found that the inflow hydrograph peak Froude number, Fpi , time-to-peak, tp and base-to-peak flow ratio, Qb / Qp and the cross-sectional shape parameter, β, all have a definite effect on kinematic shock development. The size of the wave is perhaps mostly responsible for the occurrence or nonoccurrence of the shock. Kinematic waves (as opposed to diffusion waves) are more prone to shock development, as are waves with a low Qb / Qp ratio. High Froude number flows are somewhat more conducive to shock development than low Froude number flows. Wide rectangular channels show a much stronger tendency for wave steepening than either triangular or narrow channels. Low values of β (β approaching 1.0) increase wave diffusion and inhibit shock development.
Given the foregoing results, it is concluded that kinematic shock will be most likely to occur under the following conditions: (1) A kinematic wave; (2) a low base-to-peak flow ratio; (3) a high Froude number flow; and (4) a wide and sufficiently long channel. Whether all these conditions are met remains to be assessed for individual cases. For example, a flood wave traveling in a steep, initially dry channel satisfies most of these conditions, making it a likely case for shock development.
The preceding findings can help to explain the demonstrated absence of kinematic shock in flood plain routing computations. As water levels lise above flood stage, the wetted perimeter increases at a faster rate than for inbank flows, triggering a decrease in the value of β. This effectively counteracts the steepening tendency and arrests kinematic shock development.
APPENDIX I. REFERENCES
Borah, D. K., N. Prasad, N., and C. Alonso. 1980.
"Kinematic wave routing incorporating shock fitting," Water Resources Research,
Vol. 16, No. 3, June, 529-541.
Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum method)," Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Harley, B. M., F. E.
Perkins, and P. S. Eagleson. 1970. "A modular distributed model of catchment dynamics," Report No. 133, Ralph M. Parsons Laboratory for Water Resources and Hydrodynamics,
Massachusetts Institute of Technology, Cambridge, Mass., Dec.
Kibler, D.F, and D. A.
Woolhiser. "The kinematic cascade as a hydrologic model," Hydrology Paper No. 39, Colorado State University, Fort Collins, Colo.,
Lighthill, M. J., and G. B.
Whitham. 1955. "On kinematic waves. I. Flood movement in long rivers," Proceedings, Royal Society of London, Vol. 4229, May, 281-316.
Ponce, V. M., and D. B.
Simons. 1977. "Shallow wave propagation in open channel flow," Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, Dec., 1461-1976.
Ponce, V. M., R. M. Li, and D. B.
Simons. 1978. "Applicability of kinematic and diffusion models," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, Mar., 353-360.
Ponce, V. M., and V. Yevyevich, V. 1978.
"Muskingum-Cunge method with variable parameters," Journal of the Hydraulic Division,
ASCE, Vol. 104, No. HY12, Dec., 1663-1667.
Ponce, V. M., and F. D.
Theurer, F. D. 1982. "Accuracy criteria in diffusion routing," Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY6, June, 747-757.
Ponce, V. M., 1981.
"Accuracy of physically based coefficient methods of flood routing,"
San Diego State University Civil Engineering Series, No. 83150, Aug.
Smith, R. E. "Border irrigation advance and ephemeral flood waves," Journal of the irrigation and Drainage Division, ASCE, Vol. 98, No. IR2, June, 289-307.
Tinney, E.R., and D. L. Bassett. 1951.
"Terminal shape of a shallow liquid Front," Journal of the Hydraulics Division,
ASCE, Vol. 87, No. HY5, Sept., 117-133.
APPENDIX II. NOTATION
The following symbols are used in this payer:
A = flow area;
Apr = flow area corresponding to Qpr;
B = bottom width;
do = reference flow depth;
F = Fronde number;
Fo = reference flow Froude number;
F = peak inflow Froude number;
g = gravitational acceleration;
L = wavelength;
Lc, = channel length, estimated by Eq. 6;
Lo, = reference channel length, Eq. 1;
m = integer tp / (tg - tp);
N = dimensionless number, Eq. 9;
n = Manning's friction coefficient;
Ps = shock parameter;
Q = discharge;
Qb = baseflow;
Qp = peak inflow;
Qpr = Qp - Qb;
Qt = inflow at time t;
r = ratio tp /(tg - tp );
So = channel bed slope;
Sri = slope of rising limb of inflow hydrograph, L3 / T 2 units;
Sro = slope of rising limb of outflow hydrograph, L3 / T 2 units;
t = time;
tg = time-to-center-of-gravity of inflow hydrograph;
tp = time-to-peak of inflow hydrograph;
μo = reference flow mean velocity;
VI = inflow hydrograph volume above base flow, Eq. 5;
z = channel side slope (z horizontal - 1 vertical);
α = coefficient in Q-A relation, Eq. 3;
β = exponent in Q-A relation, Eq. 3; and
σ = dimensionless wave number, σ = 2π (Lo / L).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220711 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |