1.  INTRODUCCIÓN

Este documento informa sobre una corrida de pruebas destinadas a desarrollar procedimientos mejorados para el enrutamiento de cuencas. El objetivo es comparar modelos cinemáticos y de difusión dentro de varios escenarios de realidad física y numérica. Los efectos de la pendiente de fondo y el número de Courant se identifican específicamente en este documento.

2.  TEORÍA

La ecuación de onda cinemática es la base de la mayoría de los modelos de enrutamiento de cuencas actualmente en uso. Para derivar la ecuación de onda cinemática, la declaración habitual de conservación de la masa en un volumen de control se combina con una forma simplificada de conservación del momento que solo tiene en cuenta las fuerzas de fricción y gravedad. Esto conduce a lo siguiente:

∂Q          ∂Q   _____ + c _____  =  c qL   ∂t            ∂x

(1)

en la cual Q = caudal; c = celeridad de las onda cinemática; q_L = caudal de entrada lateral, por unidad de longitud del canal; x = variable espacial; y t = variable temporal.

La Ecuación 1 se puede discretizar en el plano x-t de varias maneras. Ponce (3) identificó tres esquemas totalmente descentrados: (1) Esquema Ι, hacia adelante en el tiempo/hacia atrás en el espacio, estable para números de Courant menores que 1 y convergente a medida que el número de Courant aumenta a 1; (2) Esquema ΙΙ, adelante en el espacio/atrás en el tiempo, estable para números de Courant mayores que 1 y convergente cuando el número de Courant disminuye a 1; y (3) Esquema ΙΙΙ, incondicionalmente estable pero no convergente para todos los números de Courant.

Estos y otros esquemas similares son conocidos ampliamente como soluciones de ondas cinemáticas. Los esquemas Ι y ΙΙ son complementarios; sus versiones tienen un amplio uso, por ejemplo, en la opción de enrutamiento de ondas cinemáticas de HEC-HMS (1). Esquema ΙΙΙ (y versiones relacionadas), aunque no convergente, también se ha favorecido debido a su característica de estabilidad incondicional (2).

Ponce (3) ha aplicado el concepto de difusividad física y numérica al problema de enrutamiento de cuencas distribuidas. Comparó la solución del esquema ΙΙΙ, con su difusión numérica asociada "no controlada", con la de un esquema con difusividades coincidentes (en adelante denominado esquema ΙV), bajo una amplia gama de resoluciones de malla. Mientras que el esquema ΙΙΙ se demostró que era muy sensible al tamaño de la malla, el esquema ΙV no lo era. Esto llevó a Ponce a sugerir que el esquema ΙV era mejor que el esquema ΙΙΙ.

En el esquema ΙV, la difusividad física viene dada por:

q   ν  =  _____          2So

(2)

en las cuales ν = difusividad física; q = descarga unitaria; y S_o = pendiente de fondo.

La combinación de difusividades físicas y numéricas lleva al número de Reynolds de la malla:

q   D  =  _________           So c ∆s

(3)

en la cual D = número de Reynolds de la malla; y ∆s = intervalo de espacio (∆x o ∆y).

Al incluir la dependencia del número de Froude en la difusividad física, Ponce (3) extendió el concepto de difusividades al ámbito de las ondas dinámicas. Esto condujo al modelo dinámico de difusión (denominado aquí modelo dinámico), que es el mismo que el esquema ΙV pero con el número de Reynolds de la malla definido de la siguiente manera:

q   D  =  _________ [ 1 - ( β - 1 ) 2 F 2 ]           So c ∆s

(4)

en la cual β = exponente de la curva de gasto (relación de área-caudal); y F = número de Froude.

3.  ESTRATEGIA DE ESTUDIO

En este artículo se examina la sensibilidad de la respuesta de la cuenca al modelo de enrutamiento, la pendiente de fondo y el número de Courant. Se eligen tres modelos de enrutamiento: (1) Esquemas Ι/ΙΙ, con el esquema Ι utilizado para números de Courant menores o iguales a 1, y el esquema ΙΙ utilizado para números de Courant superiores a 1, en adelante modelo de onda cinemática; (2) esquema ΙV, con difusividades físicas y numéricas combinadas, en lo sucesivo denominado modelo de onda de difusión; y (3) el modelo de difusión con dinámica, es decir, el esquema ΙV, pero con difusividad dependiente del número de Froude (Ec. 4), en adelante denominado modelo de onda dinámica. Dado los resultados de Ponce (3), la excesiva y descontrolada difusión numérica del esquema ΙΙΙ impidió su consideración.

Se eligieron tres pendientes de fondo y tres números de Courant, los cuales abarcan un rango de valores que probablemente se encuentren en la práctica. Las combinaciones de modelos, pendientes de fondo y números de Courant llevaron a un programa de veintisiete (27) simulaciones.

4.  EXPERIMENTOS NUMÉRICOS

Se diseñaron experimentos numéricos para probar la sensibilidad de la respuesta de la cuenca al modelo, la pendiente de fondo y el número de Courant. Se desarrolló un ejemplo hipotético adecuado a los objetivos generales del estudio. El ejemplo consistió en una cuenca conceptualizada como un libro abierto con dos planos adyacentes a un canal. Se supone que los planos son impermeables, con un exceso de precipitación (precipitación efectiva) igual a la precipitación total. El ingreso a los planos es el exceso de precipitación, y la escorrentía es por flujo superficial en una dirección perpendicular a la alineación del canal. El flujo de entrada al canal es por contribución lateral de los planos, y el flujo de salida del canal es la respuesta de la cuenca (3).

Las dimensiones son: longitud del plano (en la dirección del flujo del plano) = 600 pies (183 m); longitud del canal = 1200 pies (366 m). La precipitación es de 76.2 mm/h (3 in/hr), el cual cuando se multiplica por el área de captación da como resultado un caudal máximo de 100 cfs (2.83 m³/s).

Se seleccionaron los siguientes valores de pendiente de fondo: (1) suave, 0.0001; (2) promedio, 0.001; y (3) empinada, 0.01. Los números de Courant elegidos fueron: 0.5, 1 y 2. Para estas pendientes de fondo y números de Courant, las velocidades de onda y los intervalos discretos (∆x, ∆y, y ∆t) fueron elegidos para producir una corrida consistente de 27 simulaciones (Tabla 1).

Dada la geometría de la cuenca, la trayectoria del flujo y la celeridad de las ondas, la duración de la precipitación se igualó al tiempo de concentración, asumiendo el tiempo de translación cinemático, y despreciando la difusión. En consecuencia, para la pendiente suave (0.0001), la duración de la lluvia se fijó en 240 minutos, con un volumen de escorrentía de 1,440,000 pies³ (40,776 m³); para la pendiente media (0.001) se fijó en 120 minutos, con un volumen de escorrentía de 720,000 pies³ (20,388 m³); y para la pendiente pronunciada (0.01) se fijó en 60 minutos, con un volumen de escorrentía de 360,000 pies³ (10.914 m³).

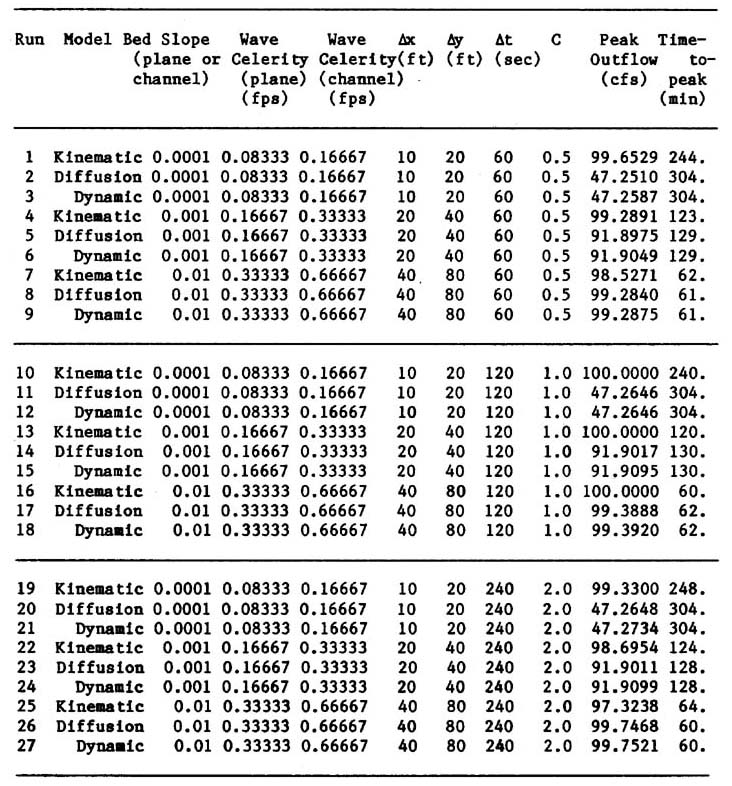
Para este estudio se fijó el valor de β para flujo plano en 3, característico del flujo laminar, mientras que el valor para flujo en canal se fijó en 1.5, característico de la fricción turbulenta de Chezy. Las velocidades medias de flujo se calcularon dividiendo las velocidades de onda por los valores de β. Las profundidades de flujo promedio se calcularon asumiendo flujo laminar en los planos y flujo turbulento en el canal.

5.  RESULTADOS

La Tabla 1 muestra los resultados de las simulaciones 1 a 27, expresados en términos de flujo pico de salida y tiempo hasta el pico. Estos resultados conducen a las siguientes conclusiones con respecto al efecto del modelo, la pendiente de fondo y el número de Courant en la respuesta de la cuenca:

•          Modelo

1. Modelos cinemáticos y de difusión: Para la pendiente suave, las diferencias en el flujo de salida pico entre los modelos cinemáticos y de difusión son muy grandes (consulte, por ejemplo, 99.6529 para la corrida 1 frente a 47.2510 para la corrida 2); para la pendiente media, las diferencias son grandes (99.2891 para la corrida 4 frente a 91.8975 para la corrida 5); y para la fuerte pendiente, las diferencias son pequeñas, tendiendo a enmascararse por la falta de difusión física (100.000 para la corrida 16 vs 99.3888 para la corrida 17).

2. Modelos de difusión y dinámico: Las diferencias en el flujo de salida pico entre los modelos de difusión y dinámico son bastante pequeñas, independientemente de la pendiente o el número de Courant (consulte, por ejemplo, 47.2510 para la corrida 2 frente a 47.2587 para la corrida 3; también 91.9017 para la corrida 14 frente a 91.9095 para la corrida 15).

   • Pendiente de fondo

3. Modelo cinemático: La pendiente de fondo generalmente tiene poco efecto en el flujo de salida pico (por ejemplo, 99.6529 para la corrida 1, frente a 99.2891 para la corrida 4, y frente a 98.5271 para la corrida 7). Para un número de Courant igual a 1, la pendiente de fondo no tiene efecto sobre el flujo de salida pico (100 para las ejecuciones 10, 13 y 16). El flujo de salida pico de 100 cfs (2,83 m³/s) representa la translación cinemática pura, es decir, la ausencia total de difusión y/o dispersión numérica.

4. Modelos dinámicos y de difusión: La pendiente de fondo tiene un efecto considerable en el flujo de salida pico (ver, por ejemplo, 47.2510 para la corrida 2, frente a 91.8975 para la corrida 5, y frente a 99.2840 para la corrida 8; también, comparar 47.2646 para la corrida 12, frente a 91.9095 para la corrida 15, y frente a 99.3920 para la corrida 18). Cuanto menor sea la pendiente del lecho, mayor será la difusión experimentada por el hidrograma.

   • Número de Courant

5. Modelos cinemáticos: Para un número de Courant igual a 1, hay una ausencia total de difusión y/o dispersión numérica, con un pico de salida igual a 100 y un tiempo hasta el pico igual a la duración de la precipitación (véanse las simulaciones 10, 13 y 16). Para números de Courant distintos de 1 (es decir, 0.5 y 2), hay un pequeño efecto numérico de difusión/dispersión (99.6529 para la corrida 1, y 99.3300 para la corrida 19), atribuido a la alta resolución de la malla utilizada en estas ejecuciones.

6. Modelos dinámicos y de difusión: La variación en los números de Courant tiene muy poco efecto en los modelos dinámicos y de difusión (comparar 99.2840 para la corrida 8, frente a 99.3888 para la corrida 17, y frente a 99.7468 para la corrida 26; también comparar 47.2587 para la corrida 3, frente a 47.2646 para la corrida 12, y frente a 47.2734 para correr 21). Esto se atribuye a la independencia de la malla de estos dos modelos a través de una amplio rango de números de Courant.

Tabla 1.  Corridas, modelos, pendiente de fondo, número de Courant y resumen de resultados.

6.  EFECTO DE DIFUSIÓN Y RESPUESTA DE LA CUENCA

El efecto de la difusión en la respuesta de la cuenca merece un análisis más detallado. Los resultados de las pruebas han demostrado claramente que la pendiente del lecho (ya sea del plano o del canal) tiene una influencia importante en la cantidad de difusión física experimentada por el hidrograma de salida. La experiencia adicional con el modelo de difusión ha llevado a las siguientes conclusiones: (1) Para pendientes pronunciadas, la difusión del hidrograma es pequeña; para pendientes medias, es moderada; y para pendientes suaves, es grande. En igualdad de condiciones, cuanto menor sea la pendiente del lecho, mayor será el efecto de difusión experimentado por el hidrograma de salida; (2) El efecto de difusión provoca un retraso en el flujo de salida máximo y un aumento en el tiempo de base. Cuanto mayor sea el efecto de difusión, más tardará el hidrograma de salida en alcanzar su valor máximo; por lo tanto, mayor será el tiempo de base.

En general, la respuesta de la cuenca es una función de los siguientes parámetros de tiempo: (1) duración de la precipitación t_r; (2) tiempo de concentración cinemático t_c; y (3) tiempo de concentración efectivo t_e. Para cada cuenca y evento, existe un valor máximo de flujo de salida pico, calculado como el producto de la intensidad de precipitación por el área de la cuenca. Junto con la intensidad, la duración de la precipitación representa el volumen total de escorrentía.

El tiempo de concentración cinemático es similar al concepto bien establecido de tiempo de concentración, es decir, el tiempo más largo que tarda una gota de agua en viajar desde la cabecera de la cuenca hasta la salida, sin tener en cuenta los efectos de difusión. Tiene en cuenta el tamaño y la forma de la cuenca, la velocidad media y la fricción de fondo. El tiempo de concentración efectivo incluye el efecto de difusión, y generalmente es mayor que el tiempo de concentración cinemático.

Según los valores relativos de la duración de la precipitación, el tiempo de concentración cinemático y el tiempo de concentración efectivo, el hidrograma de salida de la cuenca puede ser cinemático o difusivo, y puede estar subconcentrado, concentrado o superconcentrado.

El flujo cinemático es aquél para el cual el tiempo de concentración efectivo es igual al tiempo de concentración cinemático, es decir, cuando no hay un efecto de difusión mesurable. El flujo difusivo es aquél para el cual el tiempo de concentración efectivo es mayor que el tiempo de concentración cinemático. (El flujo con tiempo de concentración efectivo menor que el tiempo de concentración cinemático implica difusividad negativa, lo cual es claramente una imposibilidad física).

El flujo subconcentrado se define como el flujo en la cual la duración de la precipitación es menor que el tiempo de concentración efectivo ; en consecuencia, el flujo de salida máximo es menor que el valor máximo pico. El flujo concentrado se define como el flujo en el cual la duración de la lluvia es igual al tiempo de concentración efectivo, con un flujo de salida máximo igual al valor máximo pico. El flujo superconcentrado se define como el flujo en el cual la duración de la precipitación es mayor que el tiempo de concentración efectivo; el flujo de salida máximo es igual al valor máximo pico.

7.  MODELOS DIFUSIVOS VS DINÁMICOS

Se ha demostrado que los modelos de difusión y dinámicos dan prácticamente los mismos resultados, con poco que ganar usando la difusividad dependiente del número de Froude. Este comportamiento, característico de una amplia gama de pendientes de fondo, de empinadas a leves, se puede explicar de la siguiente manera: Para pendientes de lecho empinadas, es probable que el flujo sea cinemático, con soluciones difusivas y dinámicas que convergen a la solución cinemática. Para taludes de lecho leves, es probable que el flujo esté muy por debajo del crítico; por lo tanto, caracterizado por números de Froude pequeños. A medida que el número de Froude se aproxima a cero, la solución de onda dinámica converge a la solución de onda difusiva (Ecs. 3 y 4). Esto explica la ausencia de una diferencia sustancial entre las soluciones de ondas difusivas y dinámicas.

8.  RESUMEN Y CONCLUSIONES

Los modelos de ondas cinemáticas, de difusión y dinámicas se prueban bajo una amplia gama de pendientes de fondo y números de Courant. El modelo cinemático utiliza una discretización descentrada de la ecuación de onda cinemática. El modelo de difusión se formula haciendo coincidir las difusividades físicas y numéricas, lo que le da independencia de malla para una amplia gama de niveles de resolución. El modelo dinámico es una extensión del modelo de difusión teniendo en cuenta la dependencia de la difusividad con el número de Froude.

Los resultados muestran las claras ventajas de utilizar la onda difusiva en lugar de la onda cinemática. El modelo cinemático no tiene en cuenta el efecto de la pendiente de fondo, lo que lo hace inadecuado como modelo general del comportamiento de la cuenca. Los modelos de difusión y dinámicos, sin embargo, explican adecuadamente el efecto de la pendiente del fondo, produciendo la difusión como lo requiere la física del fenómeno. Para número de Courant igual a 1, el modelo cinemático muestra una completa ausencia de difusión y/o dispersión numérica. Los modelos de difusión y dinámicos, sin embargo, muestran independencia de malla a través de una amplia gama de números de Courant.

A la luz de estos hallazgos, se recomienda el modelo de difusión como un modelo general del comportamiento de una cuenca. El modelo cinemático debe usarse sólo en casos en los cuales el efecto de difusión es insignificante. Generalmente, hay muy poco que ganar usando el modelo dinámico en lugar del modelo difusivo. En la práctica, las incertidumbres con respecto a la representación adecuada de la fricción enmascararían el pequeño aumento en la precisión obtenido con el modelo dinámico.

BIBLIOGRAFÍA

1. "HEC-1, Flood Hydrograph Package, Users Manual." 1985. The Hydrologic Engineering Center, U.S. Army Corps of Engineers, Davis, Calif., Sept., 1981, revised Jan., 1985.

2. Huang, Y. H. 1978. "Channel Routing by Finite Difference Method," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY10, Oct., 1379-1393.

3. Ponce, V. M. 1986. "Diffusion Wave Modeling of Catchment Dynamics," Journal of Hydraulic Engineering, ASCE, Vol. 112, No. 8, Aug., 716-727.