1.  INTRODUCCIÓN

El cálculo de los hidrogramas de flujo superficial está bien establecido en la hidrología de avenidas. Los primeros enfoques tenían una clara base conceptual (Horton, 1938, 1945; lzzard, 1944, 1946), mientras que los enfoques más recientes, entre ellos la onda cinemática, se han basado en la física de los fenómenos (Wooding, 1965; Woolhiser y Liggett, 1967 ). La onda cinemática carece de difusión y, por lo tanto, no es adecuada para el flujo superficial en pendientes suaves, en la cual la difusión tiene un rol importante. Por otro lado, el modelo conceptual tiene una capacidad intrínseca de difusión, lo cual explica por qué el tiempo de equilibrio de referencia es el doble que el de la onda cinemática (Ponce, 1989).

En este artículo se presenta un modelo conceptual de hidrogramas adimensionales de flujo superficial. El procedimiento generaliza el enfoque clásico de Horton-Izzard para una amplia gama de exponentes de la curva de gasto, incluidos m = 3/2 y 5/3, los cuales no parecen no haber sido calculados previamente. Las curvas ascendentes y de recesión de los hidrogramas adimensionales de flujo superficial se calculan para los siguientes valores del exponente de la curva de gasto: (1) embalse lineal, m = 1, que describe una condición en la que la velocidad del flujo superficial es sensiblemente constante (Houton, 1938); (2) 100% fricción turbulenta de Chezy, m = 3/2; (3) 100% de fricción turbulenta de Manning, m = 5/3; (4) 67% de fricción turbulenta de Chezy (equivalente a un 75% de Manning turbulento), m = 2; y (5) 100% flujo laminar, m = 3.

2.  MODELO CONCEPTUAL

La escorrentía en el plano de flujo superficial se describe mediante la ecuación diferencial de almacenamiento:

dS            I - O  =  _____                dt

(1)

en la cual I = flujo de entrada, O = flujo de salida, y dS / dt = razón de cambio de almacenamiento en el plano.

Un balance de masa conduce al flujo de salida de equilibrio:

qe = iL

(2)

en la cual i = exceso de precipitación, y L = longitud del plano. Para la curva descendente, I = iL, y O = q, a partir del cual:

dS            iL - q  =  _____                 dt

(3)

Para la curva descendente, I = 0, y O = q, a partir del cual:

dS            -q  =  _____            dt

(4)

El modelo Horton-Izzard se basa en la curva de descarga-volumen de almacenamiento:

q = a S m

(5)

en la cual a y m son coeficiente y exponente, respectivamente. Se supone que la Ec. 5 es aplicable a cualquier descarga, incluida la de equilibrio. Además, el volumen de almacenamiento de equilibrio es igual a:

qe te            Se  =  _______               2

(6)

en la cual t_e = tiempo de referencia al equilibrio. Debido a la difusión de la escorrentía, la salida de equilibrio se aproxima asintóticamente, es decir, q → q_e conforme t → ∞. Por tanto, el tiempo de referencia al equilibrio es menor que el tiempo real al equilibrio, el cual tiende al infinito. Para la curva ascendente, el modelo conceptual generalizado es el siguiente:

dS            a Sem - a Sm =  _____                            dt

(7)

La solución de la Ec. 7 es (Dooge, 1973; Ponce, 1989):

1          1 t*  = ____ ∫ ______ d ( q* 1/m )           2      1 - q*

(8)

en la cual t_* = t / t_e, con t = tiempo acumulado desde el inicio del ascenso, y t_e = tiempo de referencia hasta el equilibrio, en la curva ascendente, y q_* = q / q_e, con q = el flujo de salida en el momento t, y q_e = el flujo de salida de equilibrio.

Para la curva descendente, el modelo conceptual generalizado es el siguiente:

dS            - a Sm  =  _____                   dt

(9)

La solución para la curva descendente depende de si la curva ascendente ha alcanzado el equilibrio o no. Primero, suponiendo que la curva ascendente está en equilibrio, la solución de la Ec. 9 es (Dooge, 1973):

1         1 t*  = - ___  ∫ _____ d ( q* 1/m )             2        q*

(10)

en la cual t_* = t / t_e, con t = el tiempo acumulado a partir del inicio de la recesión, y t_* = el tiempo de referencia hasta el equilibrio (de la curva ascendente); y q_* = q /q_e, con q = el flujo de salida en el momento t, y q_e = el flujo salida al inicio de la recesión, es decir, el flujo de salida de equilibrio.

Suponiendo que el flujo pico de salida al final de la curva ascendente es q_p, menor que el flujo de salida de equilibrio (q_e), la solución de la Ec. 9 es:

1        qp                            1 t*  = - ___ ( _____ ) (1 - m) / m   ∫ ____ d ( q* 1/m )             2        qe                           q*

(11)

en la cual t_* es el mismo que en la Ec. 10, pero ahora q_* = q / q_p.

La Ecuación 8 se evalúa aquí para valores de m iguales a 1, 3/2, 5/3, 2 y 3.

1.  m = 1             1            t*  = - ___ ln ( 1 - q* )             2

(12)

2.  m = 3/2               1                          1                          1 t*  = - ______ { arctan ( ______ ) - arctan [ ______ ( 1 + 2 q*1/3 ) ] }            (3)1/2                   (3)1/2                    (3)1/2        1                                   1 - ( ___ ) ln ( 1 - q*1/3 ) + ( ___ ) ln ( 1 + q*1/3 + q*2/3 )        3                                   6

(13)

3.  m = 5/3 t* = - 0.3 ln ( 1 - q*1/5 ) + 0.3 cos ( 0.6 π ) ln [1 + q*2/5 + 2 q*1/5 cos ( 0.2 π )] + 0.3 cos (1.8 π ) ln [ 1 + q*2/5 + 2 q*1/5 cos (0.6 π )]                                               q*1/5 + cos (0.2 π) + 0.6 sin (0.6 π ) { arctan [ _____________________] - 0.3 π }                                                     sin (0.2 π)                                               q*1/5 + cos (0.6 π) + 0.6 sin (1.8 π ) { arctan [ _____________________] + 0.1 π }                                                     sin (0.6 π)

(14)

4.  m = 2           1            1 + q*1/2 t* = ____ ln ( ____________)           4            1 - q*1/2

(15)

5.  m = 3           1            1 + q*1/3 + q*2/3 t* = ____ ln [ ____________________]           4                ( q*1/3 - 1 ) 2          1              π                           1 - __________ { _____ + arctan [ - _______ (1 + 2 q*1/3 ) ]}     2 (3)1/2          6                        (3)1/2

(16)

Siguiendo a Dooge (1973), la solución de la Ec. 10 para m = 1 y m > 1 es:

1.  m = 1             1            t*  = - ___ ln q*             2

(17)

2.  m > 1                   1            t*  = - ____________ ( q*(1 - m) / m - 1 )             2 ( m - 1 )

(18)

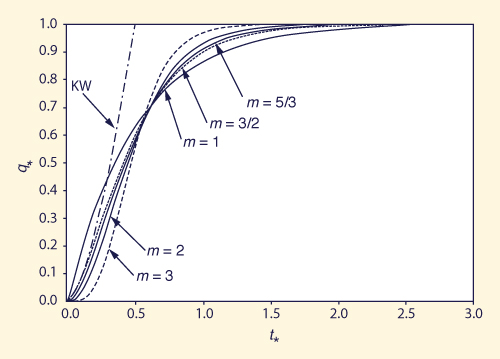
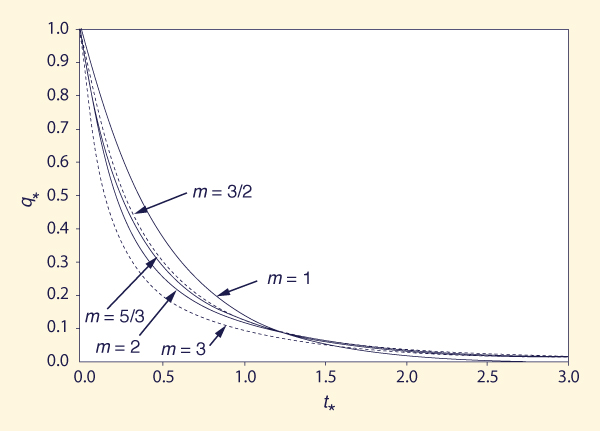
en la cual q_* = 1 en t_* = 0, es decir, el flujo de salida está en equilibrio al comienzo de la recesión.

La solución de la Ec. 11 es paralela al de la Ec. 10, pero en este caso q_* = q /q_p, y t_* se ve afectado por un factor adimensional apropiado de salida (comparar las Ecs. 10 y 11).

Las Figuras 1 y 2 muestran los hidrogramas adimensionales de flujo superficial de las curvas ascendente y de recesión calculados con las Ecs. 12 a 16 y Ecs. 17 y 18, respectivamente. También se incluye en la Fig. 1 la curva ascendente del modelo de flujo superficial de la onda cinemática, para m = 3/2, expresado en términos de t_* para comparar (Ponce, 1989):

1            t*  =  ___ q*1/m            2

(19)

Como muestra la Figura 1, los modelos conceptuales de flujo superficial tienen soluciones asintóticas y, por lo tanto, se puede simular la difusión de la escorrentía. La Figura 1 también muestra que la difusión es mayor para m = 1, en el caso de un embalse lineal. Dentro del rango 1 ≤ m ≤ 3, la difusión es mínima para m = 3.

Fig. 1  Curva ascendente del hidrograma adimensional conceptual de flujo superficial para valores selectos del exponente m de la curva de gasto.

Fig. 2  Curva descendente del hidrograma conceptual de flujo superficial para valores selectos del exponente m de la curva de gasto.

3.  CONCLUSIONES

En este artículo se calculan los hidrogramas conceptuales adimensionales de flujo superficial correspondientes a cinco exponentes de la curva de gasto en el rango m = 1 (embalse lineal) a m = 3 (flujo laminar). Los hidrogramas resultantes muestran que es posible simular cantidades variables de difusión con los modelos conceptuales de flujo superficial, a diferencia del modelo de onda cinemática, el cual no es difusivo.

BIBLIOGRAFÍA

Dooge, J.C.I. 1973. Linear theory of hydrologic systems. Technical Bulletin 1468, US Department of Agriculture, Washington, DC, pp. 327.

Horton, R. E. 1938. The interpretation and application of runoff plot experiments with reference to soil erosion problems. Proc. Soil Sci. Soc. Am. 3, 340-349.

Horton, R. E. 1945. Erosional development of streams and their drainage basins: Hydrophysical approach to quantitative geomorphology. Bull. Geol. Soc. Am. 56, 275-370.

Izzard, C. F. 1944. The surface profile of overland flow. Trans. Am. Geophys. Union 25 (6), 959-968.

Izzard, C. F. 1946. Hydraulics of runoff from developed surfaces. Proc. Highway Res. Board, Washington, DC 26, 129-146.

Ponce, V. M. 1989. Engineering Hydrology, Principles and Practices. Prentice Hall, Englewood Cliffs, NJ.

Wooding, R. A. 1965. A hydraulic model for the catchment-stream problem. J. Hydrol. 3, 254-267.

Woolhiser, D. A., y J. A. Liggett. 1967. Unsteady one-dimensional flow over a plane - the rising hydrograph. Water Resour. Res. 3(3), 753-771.