1.  INTRODUCCIÓN

El modelo Muskingum-Cunge de enrutamiento de avenidas está bien establecido en la práctica de la ingeniería hidráulica. Puede simular la convección y difusión de las ondas de avenida de manera rápida y precisa (Cunge 1969; Ponce y Yevjevich 1978; Ponce et al. 1996). La convección se caracteriza por la celeridad de las ondas, definida como la pendiente de la curva de gasto (Seddon 1990; Chow 1959). La difusión se caracteriza por la difusividad hidráulica, definida como la mitad del caudal por unidad de ancho, dividido por la pendiente de la superficie del agua (Hayami 1951).

El modelo convencional de Muskingum-Cunge se basa en la teoría de ondas cinemáticas; por lo tanto, utiliza la pendiente de equilibrio (pendiente de fondo) en la expresión de la difusividad hidráulica. Esta suposición conduce a una curva de gasto única, lo que limita el modelo en ciertos casos. En este artículo, ampliamos el modelo Muskingum-Cunge al ámbito de la curva de gasto con histéresis. Esto se logra reformulando el algoritmo Muskingum-Cunge para usar la pendiente local de la superficie del agua y el número de Vedernikov en la expresión de la difusividad hidráulica. Esto hace posible la simulación de una curva de gasto con histéresis, la cual se asemeja más a la propagación real de la onda de avenida. Para evaluar la precisión del cálculo, se comparan las curvas de gasto con histéresis con las calculadas usando un modelo de onda dinámica (Liggett 1975; Liggett y Cunge 1975; Fread 1993).

2.  MODELO DE ENRUTAMIENTO MUSKINGUM-CUNGE

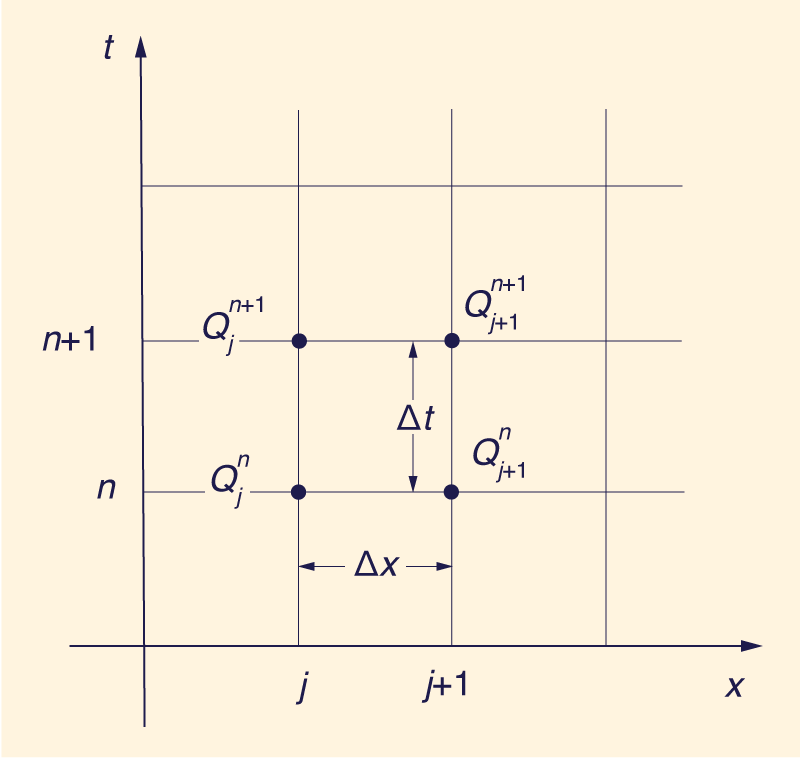
El modelo convencional de Muskingum-Cunge está bien establecido (Cunge 1969; Ponce y Yevjevich 1978; Ponce 1986; HEC-1 1990). La ecuación de enrutamiento, incluida la entrada/salida lateral, es la siguiente (Fig.1):

Fig. 1  Esquema de definición x-t para el modelo Muskingum-Cunge.

Q j+1 n+1 = C0Q j n+1 + C1Q j n + C2Q j+1 n + C3QL

(1)

en la cual j = índice espacial; n = índice temporal; y Q_L = flujo lateral (fuente o sumidero). Los coeficientes de enrutamiento son los siguientes:

-1 + C + D            C0  =  ____________             1 + C + D

(2)

1 + C - D            C1  =  ____________             1 + C + D

(3)

1 - C + D            C2  =  ____________             1 + C + D

(4)

2C            C3  =  ____________             1 + C + D

(5)

en la cual C = número de Courant, y D = número de Reynolds de la célula, respectivamente.

El número de Courant es la relación entre la celeridad de la onda de avenida c y la celeridad de la malla ∆x/∆t, de manera que:

∆t            C3  = c ____              ∆x

(6)

El número de Reynolds de la célula es la relación de la difusividad hidráulica q / (2S) (Hayami 1951) y la difusividad de la malla c∆x / 2 (Ponce y Yevjevich 1978), tal que:

q            D  =  ______          Sc∆x

(7)

en la cual q = descarga por unidad de ancho; y S = pendiente de fondo del canal.

En el modelo convencional Muskingum-Cunge, la pendiente del canal es aproxima por la pendiente del fondo (en canales prismáticos) o la pendiente de equilibrio (en canales naturales). En el modo lineal de cálculo, los parámetros de enrutamiento se basan en valores de flujo de referencia y se mantienen constantes durante todo el cálculo en el tiempo. Este modo de cálculo se denomina método de parámetro constante (Dooge 1973), para distinguirlo del método de parámetro variable, en el que los parámetros de enrutamiento pueden variar con el flujo (Ponce y Yevjevich 1978).

En el modo no lineal, los parámetros de enrutamiento se basan en valores promedio de q y c en cada celda computacional. Esto se puede lograr con un promedio directo de tres puntos de los valores en los puntos de la malla conocidos, o mediante un promedio iterativo de cuatro puntos, que incluye el punto de la malla desconocido (j + 1, n + 1) (Ponce y Chaganti 1994). Para mejorar la convergencia, se utiliza el promedio de tres puntos como primera estimación de la iteración. La pendiente del canal permanece sin cambios dentro de cada celda computacional.

Una extensión reciente del modelo Muskingum-Cunge le permite explicar parcialmente la dinámica del flujo. Esto se logra modificando la difusividad hidráulica para incluir el número de Vedernikov (Dooge et al. 1982; Ponce 1991), convirtiéndolo efectivamente en una difusividad hidráulica dinámica:

q            νd  =  ____ ( 1 - V 2 )            2S

(8)

en la cual V = número de Vedernikov, definido como la relación entre las celeridades relativas de la onda cinemática y dinámica (Vedernikov 1945, 1946; Craya 1952; Chow 1959). Así, cuando el número de Vedernikov es igual a 1, la difusividad hidráulica desaparece. Con la Ec. 8, el número de Reynolds de la célula se define de la siguiente manera:

q            D  =  _______ ( 1 - V 2 )          S c ∆x

(9)

3.  CURVA DE GASTO CON HISTÉRESIS EN EL ENRUTAMIENTO MUSKINGUM-CUNGE

Según la teoría de la propagación de las ondas de avenida, la difusión de las ondas produce invariablemente una curva de gasto con histéresis; es decir, para un tirante determinado, el caudal es mayor en la rama ascendente que en la descendente. El grosor de la histéresis aumenta a medida que la onda se vuelve más difusiva.

En los casos en los que la histéresis es significativa, su cálculo puede representar con mayor precisión la naturaleza de la propagación de ondas de avenida. En el enrutamiento Muskingum-Cunge, la curva de gasto con histéresis se puede tomar en cuenta utilizando la pendiente local de la superficie del agua en la expresión de la difusividad hidráulica.

Se desarrolló un modelo de Muskingum-Cunge de la curva de gasto con histéresis modificando el modelo de parámetros variables de cuatro puntos (Ponce y Chaganti 1994). A diferencia del modelo convencional, el modelo de curva de gasto con histéresis utiliza profundidades de flujo como parte intrínseca del cálculo. Para cada célula computacional, el procedimiento consta de los siguientes pasos:

1. Se utiliza la profundidad de flujo en el punto (j + 1, n + 1), junto con las otras tres profundidades de flujo conocidas para calcular la pendiente promedio de la superficie del agua de la celda y la profundidad media del flujo. Para mejorar la convergencia del procedimiento iterativo, el resultado del cálculo convencional de cuatro puntos se utiliza como primera aproximación de la iteración.

2. La pendiente de la superficie del agua y la profundidad de flujo se utilizan junto con la ecuación de Manning para desarrollar una curva de gasto, a partir de la cual se calculan el caudal y la celeridad de referencia.

3. La profundidad de flujo, el caudal y la celeridad de referencia se utilizan para calcular los parámetros de enrutamiento [(6) y (9)], a partir de los cuales se calculan los coeficientes de enrutamiento utilizando las Ecs. 2-5.

4. Usando (1) y los coeficientes de enrutamiento, se calcula un nuevo caudal en el punto (j + 1, n + 1).

5. La nueva descarga y la curva de gasto desarrollada en el paso 2 se utilizan para calcular una nueva profundidad de flujo en el punto (j + 1, n + 1).

6. El procedimiento se repite (pasos 1 a 5) hasta que la diferencia entre dos caudales calculados consecutivamente (en el paso 4) esté dentro de una pequeña tolerancia.

4.  EXPERIMENTOS NUMÉRICOS

Se diseñó un programa de experimentos numéricos para probar el algoritmo Muskingum-Cunge de curva de gasto con histéresis. Se asumió un canal hidráulicamente ancho para que los cálculos se pudieran realizar en términos de caudal por unidad de ancho y profundidad de flujo. Esto asegura que el enrutamiento siga siendo unidimensional, evitando así las complejidades asociadas con los desbordamientos de canales.

La pendiente de fondo se fijó en S_o = 0.0005 y una longitud de canal L = 200 km. Para esta pendiente del fondo y longitud de canal, la cantidad de difusión de la onda es suficiente para producir una curva de gasto con histéresis apreciable en el extremo aguas abajo.

Se seleccionó un coeficiente de fricción de Manning n = 0.04. Dado que el canal es hidráulicamente ancho, el exponente de la curva de gasto es β = 5/3 (Chow 1959). Se eligieron los siguientes dos valores de flujo base: q_b = 1 y 2 m²s^-1. Se eligieron las siguientes dos relaciones de flujo pico/flujo base: q_pi / q_b = 2 y 5.

Se supuso que el hidrograma de entrada es:

qpi + qb     qpi - qb          2π t qi  =  ________ - ________ cos _____                2              2                T

(10)

en la cual q_i = flujo de entrada en el tiempo t; q_pi = flujo de entrada pico; y T = período de la onda de avenida (Thomas 1934; Dooge 1973). Se eligieron los siguientes tres períodos de onda: T = 24, 48, y 96 h. Estos períodos de onda están dentro del rango de onda difusiva para estas condiciones de flujo (Ponce et al. 1978b).

Se eligieron dos niveles de resolución: Resolución Ι, con ∆x = 10 km y ∆t = 3 h; y resolución ΙΙ, con ∆x = 5 km y ∆t = 1.5 h. Con una resolución Ι, el número de pasos espaciales es 20; con una resolución ΙΙ, el número de pasos espaciales es 40. El tiempo total de simulación se fijó en cinco veces el período de la onda. El número total de pasos de tiempo es una función del nivel de resolución. (Ι o ΙΙ) y período de onda (24, 48, o 96 h). Por ejemplo, para la resolución Ι y T = 96 h, el número de pasos de tiempo es 5 × (96 / 3) = 160.

El programa de prueba varió los siguientes cuatro parámetros, para un total de 24 corridas:

1. Nivel de resolución (Ι y ΙΙ)

2. Período de la onda de avenida (24, 48, y 96 h)

3. Flujo base (1 y 2 m² s^-1)

4. relación flujo de entrada pico / flujo base (2 y 5).

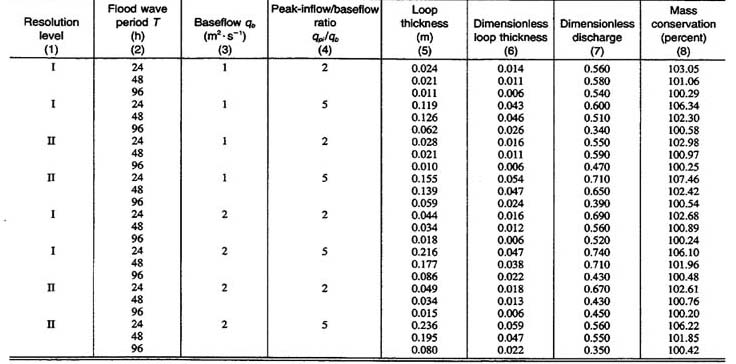
En la Tabla 1 se muestra un resumen de los resultados. Las 24 corridas mostraron una histéresis notable en la curva de gasto. El grosor de la histéresis es tomada como la diferencia máxima entre las profundidades de flujo de las curvas ascendentes y descendentes del hidrograma.

El grosor de la histéresis adimensional se define como el grosor de la histéresis dividido por el promedio de las dos profundidades de flujo (medido en el grosor de la histéresis). La descarga adimensional (en el grosor de la histéresis) se define como la diferencia entre la descarga (en el grosor de la histéresis) y el flujo base, dividida por la diferencia entre el flujo de salida máximo y el flujo base. La conservación de masa (en porcentaje) se define como la relación entre el caudal de salida y el volumen del hidrograma de entrada, excluyendo el caudal base, multiplicado por 100.

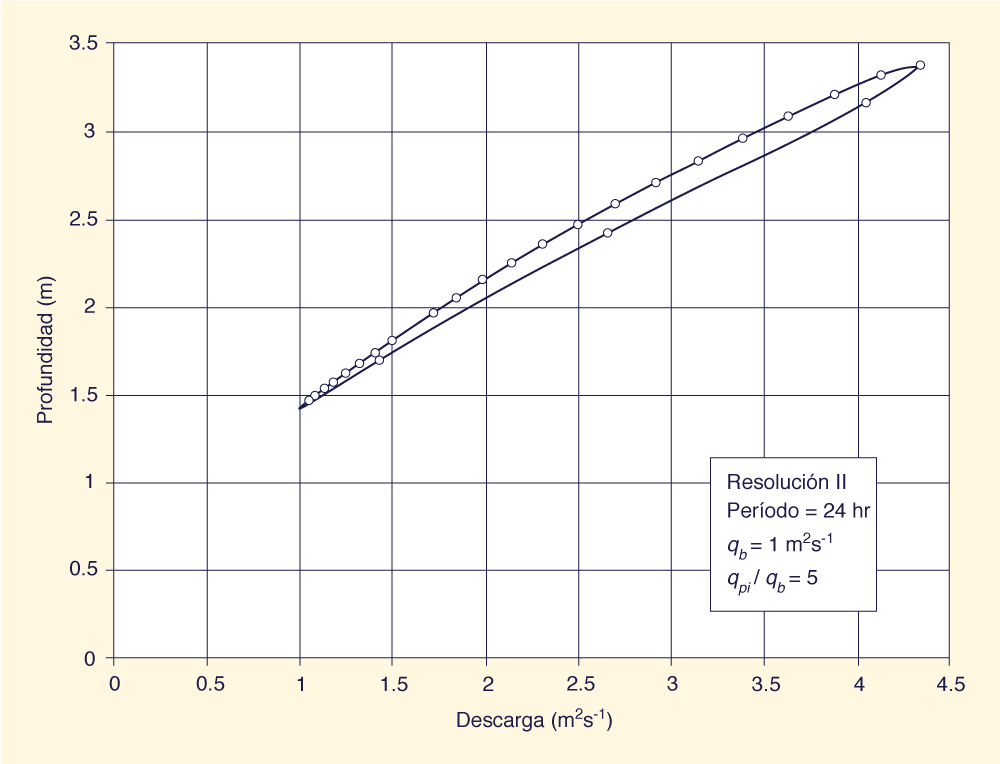
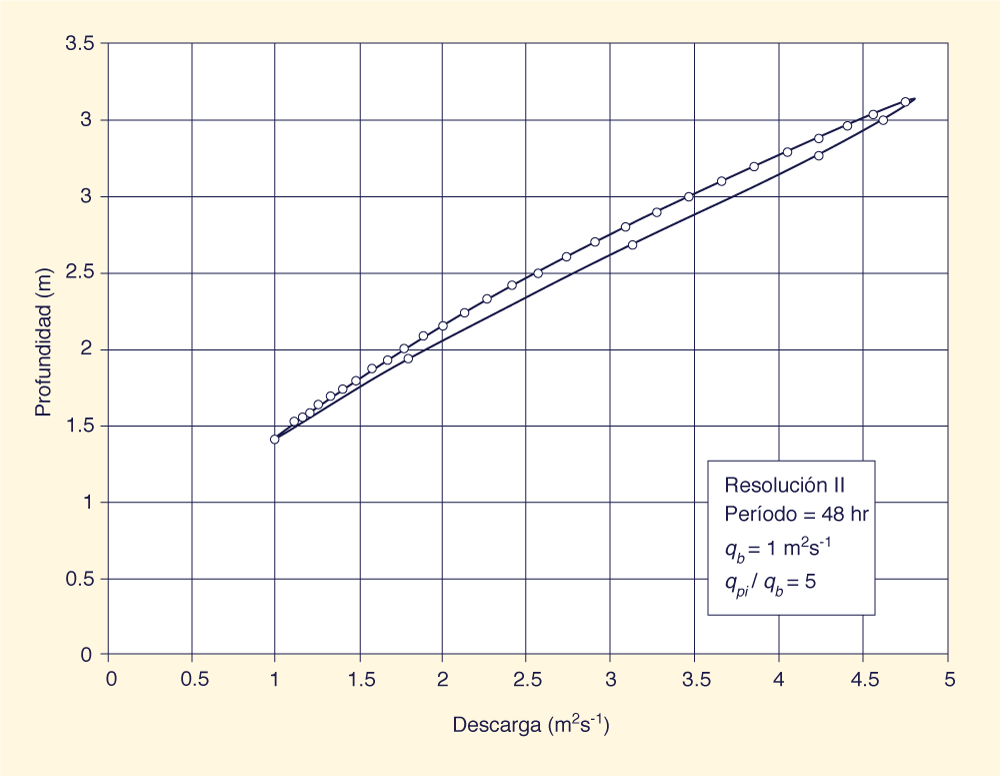
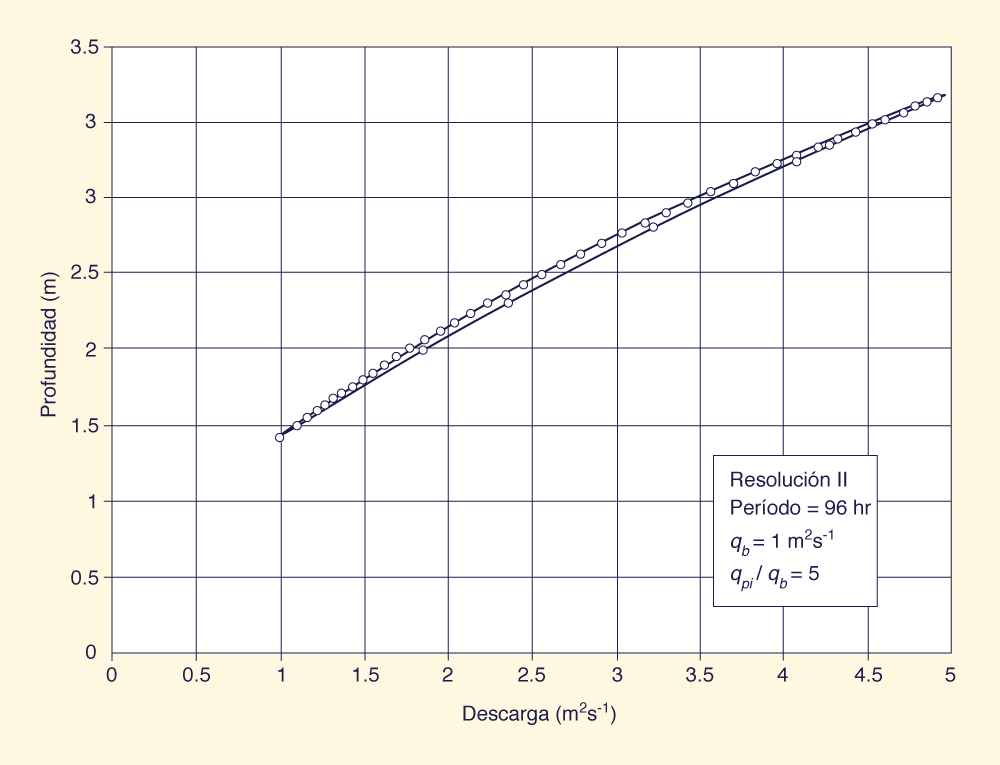
La Tabla 1 muestra que a medida que aumenta el período (Columna 2), la onda se vuelve más cinemática y el grosor de la histéresis disminuye (Columnas 5 y 6). Por el contrario, a medida que disminuye el período, la onda se vuelve más difusiva y aumenta el grosor de la histéresis. Estos resultados están de acuerdo con la teoría de la propagación de ondas de avenida (Lighthill y Whitham 1955).

El grosor de la histéresis (Columna 5) varió entre 0.010 y 0.236 m y el grosor adimensional (Columna 6) varió entre 0.006 y 0.059 (0.6% y 5.9%, respectivamente). Tanto el grosor de la histéresis como el grosor adimensional de la histéresis aumentan a medida que el flujo se vuelve más difusivo. El caudal adimensional (Columna 7) varía entre 0.35 y 0.74, estando los valores más bajos asociados a los períodos más largos, para los cuales el flujo es más cinemático.

La Tabla 1 muestra que el algoritmo de Muskingum-Cunge de la curva de gasto con histéresis tiene una ligera tendencia a ganar masa artificialmente (Columna 8). La ganancia de masa aumenta con el grosor de la histéresis y la relación de flujo de entrada pico/flujo base. Los intentos de desarrollar un algoritmo Muskingum-Cunge que produjera una curva de gasto con histéresis mientras conservaba la masa exactamente no tuvieron éxito. Se considera que la ganancia de masa relativamente pequeña está dentro de la precisión normal de los cálculos de la ingeniería hidráulica. Las Fig. 2(a) a 2(c) muestran curvas de gasto típicas con histéresis generadas por el modelo Muskingum-Cunge, correspondientes a la resolución ΙΙ; periodos de onda de 24, 48 y 96 h; flujo base de 1 m²s^-1; y una relación de flujo pico / flujo base = 5.

Tabla 1.  Resumen de resultados de la curva de gasto con histéresis en el modelo Muskingum-Cunge.

Fig. 2(a)  Curvas de gasto con histéresis típicas generadas por el modelo Muskingum-Cunge, para el período = 24 h.

Fig. 2(b)  Curvas de gasto con histéresis típicas generadas por el modelo Muskingum-Cunge, para el período = 48 h.

Fig. 2(c)  Curvas de gasto con histéresis típicas generadas por el modelo Muskingum-Cunge, para el período = 96 h.

5.  COMPARACIÓN CON EL MODELO DE ONDA DINÁMICA

La curvas de gasto con histéresis generadas por el modelo Muskingum-Cunge se compararon con las curvas de gasto generadas mediante DYNA, un modelo de onda dinámica basado en las ecuaciones de St. Venant (Ponce 1982). Una característica importante de un modelo de onda dinámica es que requiere la especificación de una condición de frontera aguas abajo. Dado que la curva de gasto con histéresis no se conoce de antemano, generalmente se asume una curva de gasto de un solo valor. Sin embargo, la curva de gasto de un solo valor contradice la solución en la frontera y afecta progresivamente los resultados calculados inmediatamente aguas arriba (Abbott 1976).

En la práctica, la curva de gasto con histéresis en la frontera aguas abajo se puede modelar de dos maneras: (1) utilizando la pendiente de fricción en lugar de la pendiente de fondo, en un procedimiento que se asemeja mucho al algoritmo Muskingum-Cunge de la curva de gasto con histéresis (Fread 1993); o (2) extendiendo artificialmente el canal para especificar una curva de gasto de un valor en una sección más aguas abajo, mientras que se le da a la histéresis la oportunidad de desarrollarse en la sección transversal de interés, localizada aguas arriba. Los análisis de sensibilidad que utilizan varias longitudes de extensión de canal pueden proporcionar una guía para determinar la longitud apropiada.

Para propósitos de comparación, un subconjunto del programa de prueba original (resolución ΙΙ; períodos de 24, 48, y 96 h; flujo base de 1 m² s^-1; y una relación de flujo pico de entrada / flujo base igual a 2) se ejecutó con el modelo de onda dinámica. Dado que la longitud del canal para el programa de prueba es de 200 km, el modelo se ejecutó utilizando longitudes de canal de 400 km y 600 km.

Un parámetro clave del esquema de Preissmann (utilizado en DYNA) es el factor de ponderación θ, el cual se utiliza para controlar la inestabilidad numérica. En teoría, un valor de θ = 0.5, aunque tiene una precisión de segundo orden, no puede controlar las inestabilidades no lineales que a menudo afectan a los cálculos de ondas dinámicas. Desplazando el esquema hacia el lado estable, es decir, aumentando el valor de θ por encima de 0.5, aumentará la estabilidad a costa de una reducción en la convergencia (O'Brien et al. 1951; Ponce et al. 1978a). En la práctica, valores de θ entre 0.5 y 0.6 se utilizan comúnmente para lograr un compromiso razonable entre estabilidad y convergencia (Fread 1993).

En el enrutamiento dinámico de ondas, la elección del factor de ponderación es responsabilidad del modelador. En nuestro caso, varios valores de θ se probaron para determinar el valor más adecuado. El valor más grande de θ eliminó la inestabilidad numérica, pero a costa de una menor convergencia (una reducción sustancial del flujo máximo). Un valor de θ = 0.55 se eligió para hacer coincidir los resultados del modelo de onda dinámica con el modelo Muskingum-Cunge de la curva de gasto con histéresis.

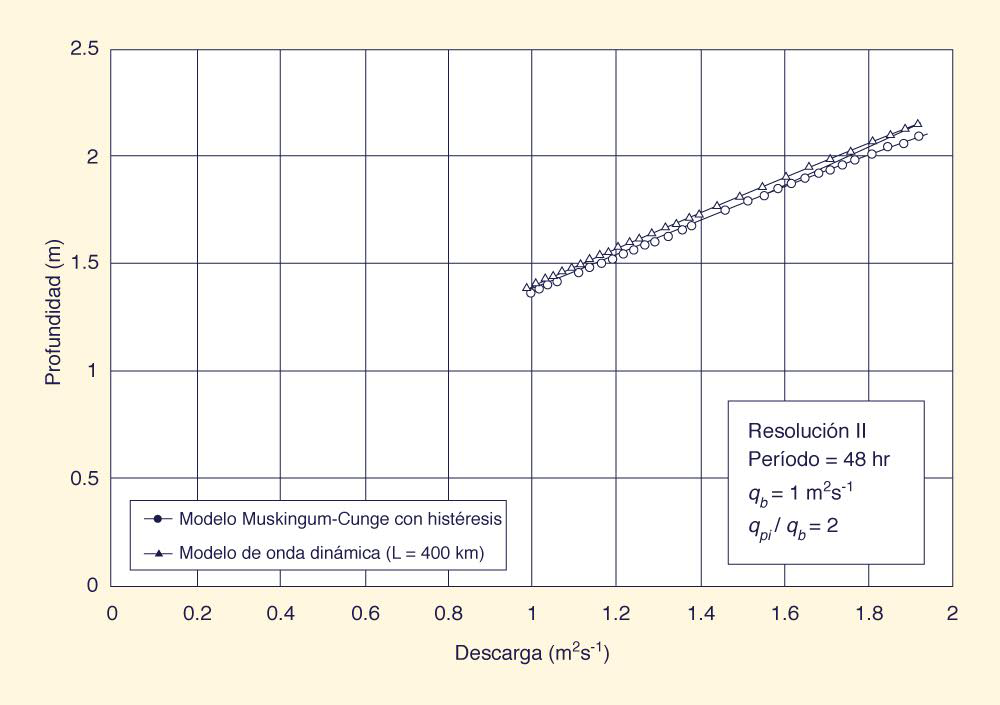
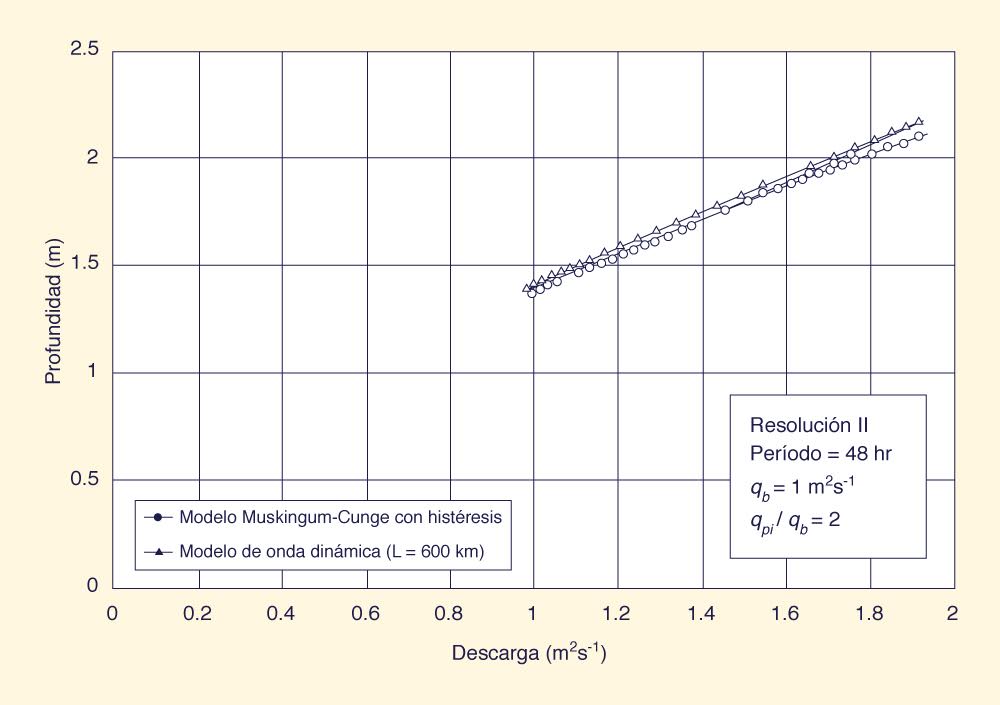
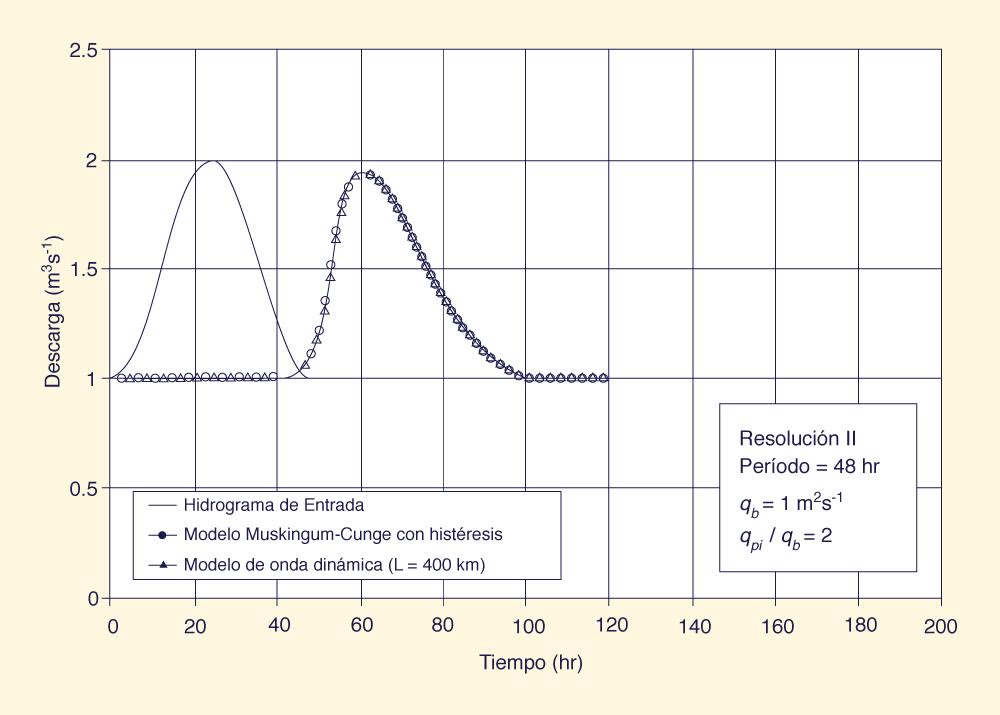
Las Figuras 3(a) y 3(b) muestran curvas de gasto con histéresis típicas para los modelos Muskingum-Cunge y de onda dinámica, a una distancia de 200 km. En el caso del modelo de onda dinámica, la curva de gasto con histéresis fue generada por la extensión artificial del canal. Las curvas de gasto con histéresis (a 200 km) para las longitudes de canal de 400 km y 600 km que se muestran en las Figs. 3(a) y 3(b) fueron esencialmente las mismas. Por lo tanto, se concluye que la longitud del canal de 400 km es suficiente para producir una curva de gasto con histéresis precisa en la sección transversal de la interés (a 200 km). La Figura 4 muestra los hidrogramas de flujo de salida para los modelos de onda dinámica y Muskingum-Cunge de la curva de gasto con histéresis. Sólo se muestran los resultados del modelo de onda dinámica para L = 400 km. Existe una concordancia sustancial entre los hidrogramas de salida calculados por ambos modelos.

Fig. 3(a)  Curvas de gasto con histéresis típicas generadas por los modelos de onda dinámica y Muskingum-Cunge a una distancia de 200 km - L = 400 km.

Fig. 3(b)  Curvas de gasto con histéresis típicas generadas por los modelos de onda dinámica y Muskingum-Cunge a una distancia de 200 km - L = 600 km.

Fig. 4  Comparación de los hidrogramas de salida generados por los modelos de onda dinámica y Muskingum-Cunge de la curva de gasto con histéresis a una distancia de 200 km.

6.  RESUMEN Y CONCLUSIONES

Se desarrolló el modelo Muskingum-Cunge de curva de gasto con histéresis reformulando el modelo convencional de cuatro puntos para usar la pendiente local de la superficie del agua y el número de Vedernikov en la expresión de difusividad hidráulica. El modelo desarrollado tuvo éxito en generar curvas de gasto con histéresis bajo una amplia gama de condiciones de flujo no permanente cinemático/difusivo, es decir, dentro del rango de aplicabilidad del método Muskingum-Cunge (Ponce et al. 1978b; Ponce y Yevjevich 1978).

Se utilizó un programa de experimentos numéricos para probar el modelo Muskingum-Cunge de curva de gasto con histéresis. El nivel de resolución, período de la onda de avenida, el flujo base y relación del flujo pico de entrada/flujo base se variaron para determinar el grosor de la histéresis, el grosor de la histéresis adimensional, la descarga adimensional y el porcentaje de conservación de masa. La comparación del modelo de Muskingum-Cunge de la curva de gasto con histéresis con el modelo de onda dinámica (DYNA) mostró que ambos modelos son capaces de generar curvas de gasto con histéresis e hidrogramas de salida con una precisión similar.

APÉNDICE I.  BIBLIOGRAFÍA

Abbott, M. A. 1976. "Computational hydraulics: A short pathology." J. Hydr. Res., Delft, The Netherlands, 14(4), 271-285.

Chow, V. T. 1959. Open-channel hydraulics, McGraw-Hill, New York.

Craya, A. 1952. "The criterion for the possibility of roll-wave formation." Gravity Waves: Circular No. 521, National Bureau of Standards, Washington, D.C., 141-151.

Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum method)." J. Hydr. Res., Delft, The Neterlands, 7(2), 205-230.

Dooge, J. C. I. 1973. "Linear theory of hydrologic systems." USDA Tech, Bull. 1468, U.S. Department of Agriculture, Washington, D.C.

Dooge, J. C. I., W. B. Strupczewski, y J. J. Napiorkowski. (1982). "Hydrodynamic derivation of storage parameters of the Muskingum model." J. Hydro., Amsterdam, 54, 371-387.

Fread, D. 1993. "Chapter 10: Flow routing." Handbook of hydrology, D. R. Maidment, ed., McGraw-Hill, New York.

Hayami, S. 1951. "On the propagation of flood waves." Disater Prevention: Res. Inst. of Kyoto Univ. Bull., Japan, 1. 1-16

HEC-1: Flood hydrograph package-User's manual, Version 4. 1990. U.S. Army Corps of Engineers, Hydrologic Engineering Center, Davis, Calif.

Liggett, J. A. 1975. "Chapter 2: Basic equations of unsteady flow." Unsteady flow in open channels, Vol. 1, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Littleton, Colo.

Liggett, J. A., y Cunge, J. A. 1975. "Chapter 4: Numerical methods of solution of the usteady flow equations." Unsteady flow in open channels, Vol. 1, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Littleton, Colo.

Lighthill, M. J., y G. B. Whitham. 1955. "On kinematic waves. Ι. Flood movement in long rivers." Proc., Royal Soc., London, 229(Ser. A), 281-316.

O'Brien, G. G., M. A. Hyman, y S. kaplan. (1951). "A study of the numerical solution of partial differential equations." J. Mathematics and Phys., 29(4), 233-251.

Ponce, V. M. 1982. DIFF / DYNA user's manual, Department of Civil Engineering, San Diego State University, San Diego.

Ponce, V. M. 1986. "Diffusion wave modelling of catchment dynamics." J. Hydr. Engrg., ASCE, 112(8), 716-727.

Ponce, V. M. 1991. "New perspective on the Vedernikov number." Water Resour. Res., 27(7), 1777-1779.

Ponce, V. M., and P. V. Chaganti. 1994. "Variable-parameter Muskingum-Cunge method revisited." J. Hydro., Amsterdam. 162, 433-439.

Ponce, V. M., A. K. Lohani, y C. Scheyhing. 1996. "Analytical verification of Muskingum-Cunge routing." J. Hydro., Amsterdam. 174. 235-241.

Ponce, V. M., D. B. Simons, y H. Indlekofer. 1978a. "Convergence of four-point implicit water wave models." J. Hydr. Div., ASCE. 104(7), 947-958.

Ponce, V. M., R. M. Li, y D. B. Simons. 1978b. "Applicability of kinematic and diffusion models." J. Hydr Div., ASCE, 104(3), 353-360.

Ponce, V. M., y V. Yevjevich, v. 1978. "Muskingum-Cunge method with variable parameters." J. Hydr. Div., ASCE, 104(12), 1663-1667.

Seddon, J. A. 1900. "River hydraulics." Trans., ASCE, Reston, Va., 43, 179-229

Thomas, H. A. 1934. "The hydraulics of flood movements in rivers." Engrg. Bull., Carnegie Institute of Technology, Pittsburgh.

Vedernikov, V. V. 1945. "Conditions at the front of a translation wave disturbing a steady motion of a real fluid." U.S.S.R. Acad. of Sci. Comptes Rendus (Doklady), 48(4), 239-242.

Vedernikov, V. V. 1946. "Characteristic features of a liquid flow in an open channel." U.S.S.R. Acad. of Sci. Comptes Rendus (Doklady), 52(3), 207-210.

APÉNDICE ΙΙ.  SIMBOLOGÍA

Los siguientes símbolos han sido utilizados en este artículo:

C = Número de Courant, (6);

C₀ = coeficiente de enrutamiento, (2);

C₁ = coeficiente de enrutamiento, (3);

C₂ = coeficiente de enrutamiento, (4);

C₃ = coeficiente de enrutamiento, (5);

c = celeridad de la onda de avenida;

D = número de Reynolds de la célula, (7) y (9);

j = índice espacial;

L = longitud del canal;

n = índice temporal [(1)], también coeficiente de fricción de Manning;

Q = caudal;

Q_L = flujo lateral (fuente o sumidero);

q = descarga por unidad de ancho;

q_b = flujo base;

q_i = flujo de entrada en el t;

q_pi = flujo de entrada pico;

q_pi / q_b = relación del flujo de entrada pico / flujo base;

S = pendiente del canal;

S_o = pendiente de fondo;

T = período de la onda de avenida;

t = tiempo;

V = número de Vedernikov;

β = exponente de la curva de gasto;

∆t = intervalo de tiempo;

∆x = intervalo de espacio;

θ = factor de ponderación del esquema de Preissmann; y

ν_d = difusividad hidráulica dinámica.