1.  INTRODUCCIÓN

El desarrollo urbano disminuye la rugosidad de la superficie y las tasas de infiltración, decreciendo así el tiempo de concentración y aumentando la escorrentía superficial. Cuando se toman en conjunto, estos efectos dan como resultado un aumento en la magnitud y frecuencia de las avenidas aguas abajo, a cualquier escala.

Para contrarrestar esta tendencia, la detención y retención de escorrentía se considera ahora una estrategia alternativa (Stahre y Urbonas 1990). El fundamento de este cambio de enfoque es el reconocimiento de que la estrategia de drenaje convencional tiene sus defectos: si bien reduce efectivamente el riesgo de inundación local, da como resultado un aumento del riesgo de inundación regional.

Aquí definimos "drenaje cinemático" como la estrategia que produce un hidrograma de tormenta el cual asciende a la velocidad más rápida posible. Por otro lado, definimos el "drenaje difusivo" como el que produce un hidrograma de tormenta que asciende a velocidades inferiores a la cinemática.

El cálculo del drenaje difusivo es posible con el modelo de cuenca de onda difusiva (Ponce 1986; Orlandini y Rosso 1996). El efecto de difusión reduce la velocidad de ascenso del hidrograma de salida, aumentando el tiempo de base, distribuyendo el flujo en el tiempo, y reduciendo el riesgo de inundación aguas abajo.

En este artículo, utilizamos el modelo de cuenca de onda difusiva para cuantificar la detención de la escorrentía en áreas de estacionamiento urbano. Se aplican cuatro tormentas extremas caracterizadas para el condado de San Diego, California, a cuatro tamaños de estacionamiento típicos, con el fin de evaluar la sensibilidad del hidrograma resultante para pendientes del terreno en el rango de 1 por ciento a 0.1 por ciento. El objetivo es determinar el efecto de la pendiente en el flujo en áreas de estacionamiento urbano.

2.  MODELO DE ONDA DIFUSIVA

El modelo de onda difusiva utilizado aquí es una extensión del método Muskingum-Cunge de enrutamiento de avenidas (Cunge 1969; "Flood" 1975) a los fenómenos de flujo superficial (Ponce 1986). La configuración geométrica sigue el libro abierto de Wooding (1965). La entrada a los planos es la intensidad de lluvia efectiva, que se convierte en un flujo lateral de entrada al canal central, el cual drena los dos planos. A su vez, la entrada lateral al canal se conduce a la salida y se expresa allí como un hidrograma de salida.

Debido a que la difusividad hidráulica es una función del número de Vedernikov (Vedernikov 1945; Chow 1959), el modelo de cuenca tiene un importante componente dinámico (Dooge 1973; Dooge et al. 1982; Ponce 1991). Por lo tanto, la difusión es igual a cero si el número de Vedernikov se acerca a uno. Sin embargo, en las condiciones de flujo que normalmente se encuentran en el flujo superficial, el número de Vedernikov suele estar muy por debajo de uno.

El método Muskingum-Cunge funciona igualando difusividades físicas y numéricas. La estabilidad numérica y la convergencia se conservan fijando el número de Courant C = 1, y variando en vez el número de incrementos espaciales. Esta técnica evita la infame caída en el hidrograma calculado (Hjelmfelt 1985) y hace posible una simulación estable y convergente. Además, la formulación lineal conserva la masa exactamente, a la vez que evita el desarrollo del choque cinemático.

A diferencia del modelo de onda cinemática, el cual es un modelo de un parámetro y, por lo tanto, responde solo a la celeridad de la onda (Seddon 1900; Chow 1959), el modelo de onda difusiva es de dos parámetros y responde tanto a la celeridad de la onda como a la difusividad hidráulica (Hayami 1951). En esencia, esto significa que el modelo de onda difusiva puede simular una característica perceptible como la difusión del flujo, la cual es directamente rastreable a la difusividad hidráulica. En contraposición, un modelo de onda cinemática no puede dar cuenta de la difusividad de manera correcta, lo que resulta en simulaciones que dependen del tamaño de la malla (Ponce 1986).

Debido a que la difusividad hidráulica está inversamente relacionada con las pendientes de los planos y del canal, el modelo de onda difusiva es adecuado para aplicaciones donde la pendiente tiene un rol importante. Cuanto más pronunciada es la pendiente, el flujo es más cinemático y menos difusivo; por el contrario, cuanto más suave es la pendiente, el flujo es más difusivo y menos cinemático. Para una pendiente lo suficientemente empinada, el flujo se vuelve cinemático y el hidrograma de salida resultante crece a la velocidad más rápida posible. Para las pendientes más suaves, el hidrograma de salida crece a velocidades inferiores a la cinemática.

El razonamiento anterior llevó a la formulación de un programa de pruebas diseñado para determinar la sensibilidad de los hidrogramas de flujo superficial a las pendientes de los planos y del canal. El objetivo es evaluar la viabilidad de utilizar la pendiente como parámetro de diseño en la gestión de aguas pluviales urbanas.

3.  PROGRAMA DE PRUEBAS Y RESULTADOS DEL MODELO

El programa de pruebas fue diseñado para variar la intensidad de la tormenta, el área de la cuenca y la pendiente de diseño para una amplia gama de condiciones. Se establecieron cuatro tipos de tormentas extremas, las cuales se muestran en la Tabla 1 para el área urbana de San Diego ("Rainfall" 1982).

Se seleccionaron cuatro tamaños de áreas de estacionamiento urbano típicos, que van desde 0.105 a 6.88 ha (Architectural 1988). Los tipos de áreas de estacionamiento se clasificaron de la siguiente manera: A = muy pequeño, 0.105 ha; B = pequeño, 0.83 ha; C = grande, 3.44 ha; y D = muy grande, 6.88 ha.

La Tabla 2 muestra los flujos de salida de equilibrio para cada tipo de tormenta y estacionamiento (Ponce 1989). Por simplicidad, la geometría elegida es el libro abierto de Wooding (1965), el cual incluye un canal de drenaje en el medio de los dos planos, de tamaño adecuado. La rugosidad de la superficie en planos y canales se estableció en n = 0.1 (HEC-1 1990) y n = 0.013 (Chow 1959), respectivamente.

Se eligieron cuatro pendientes de diseño para reflejar una amplia gama de condiciones de flujo, desde cinemático hasta difusivo. Se consideró que las pendientes inferiores al 0.1% no eran prácticas debido a la posibilidad de encharcamiento excesivo, lo que podría afectar la conducción de los automóviles. Las pendientes seleccionadas fueron las siguientes: (1) 1%, cinemática; (2) 0.5%, levemente difusiva; (3) 0.2%, moderadamente difusiva; y (4) 0.1%, fuertemente difusiva.

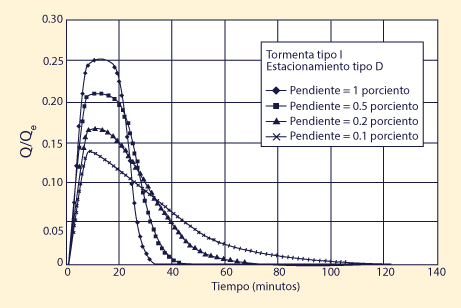
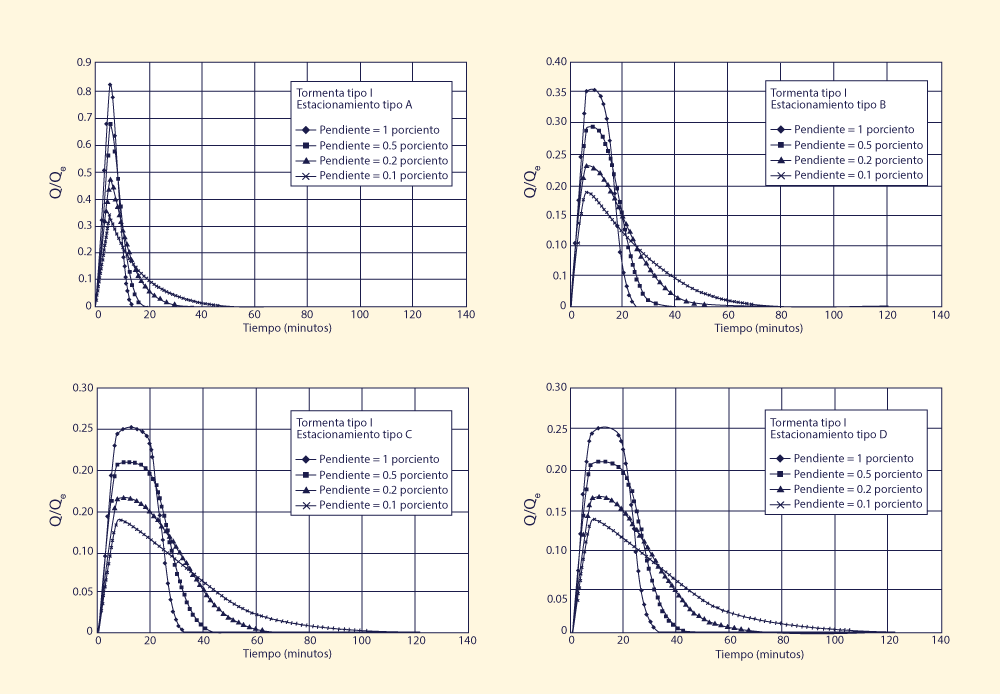
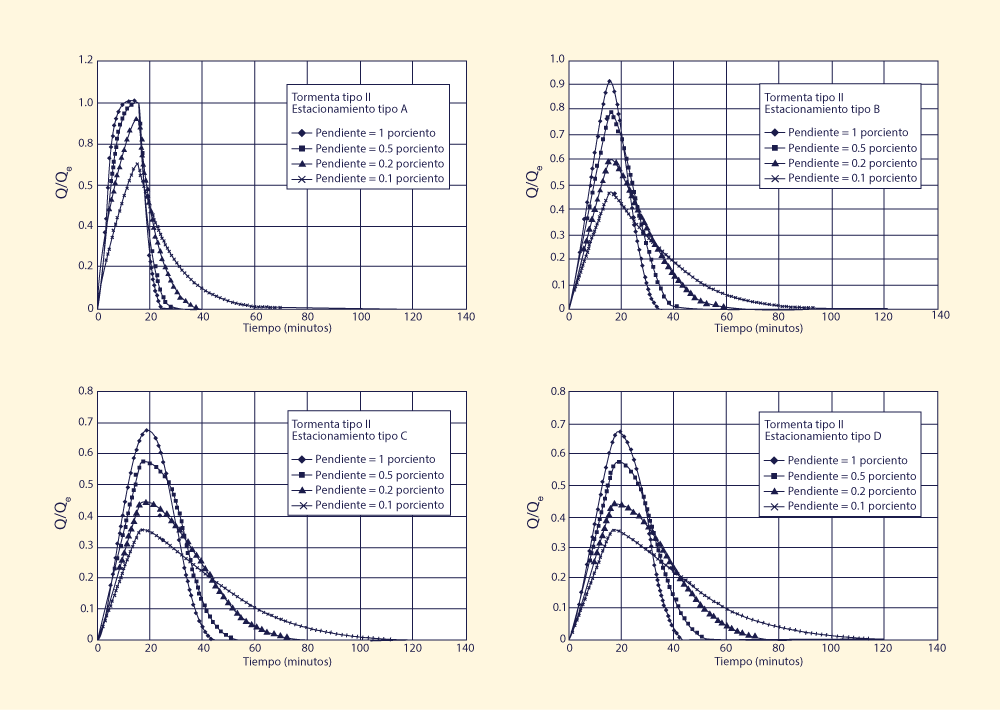
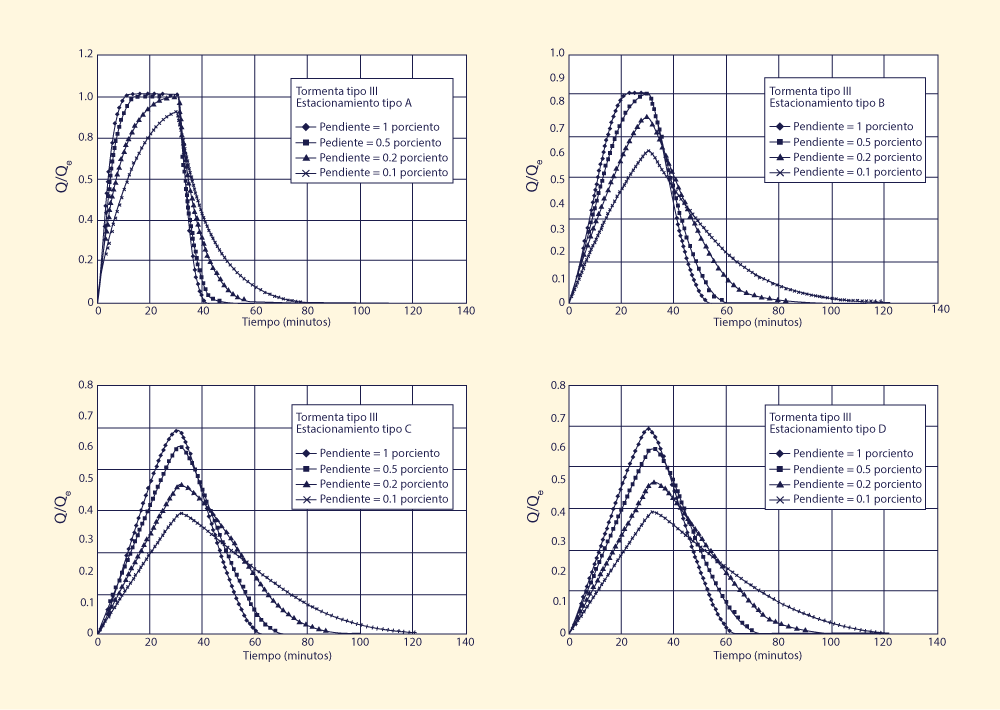
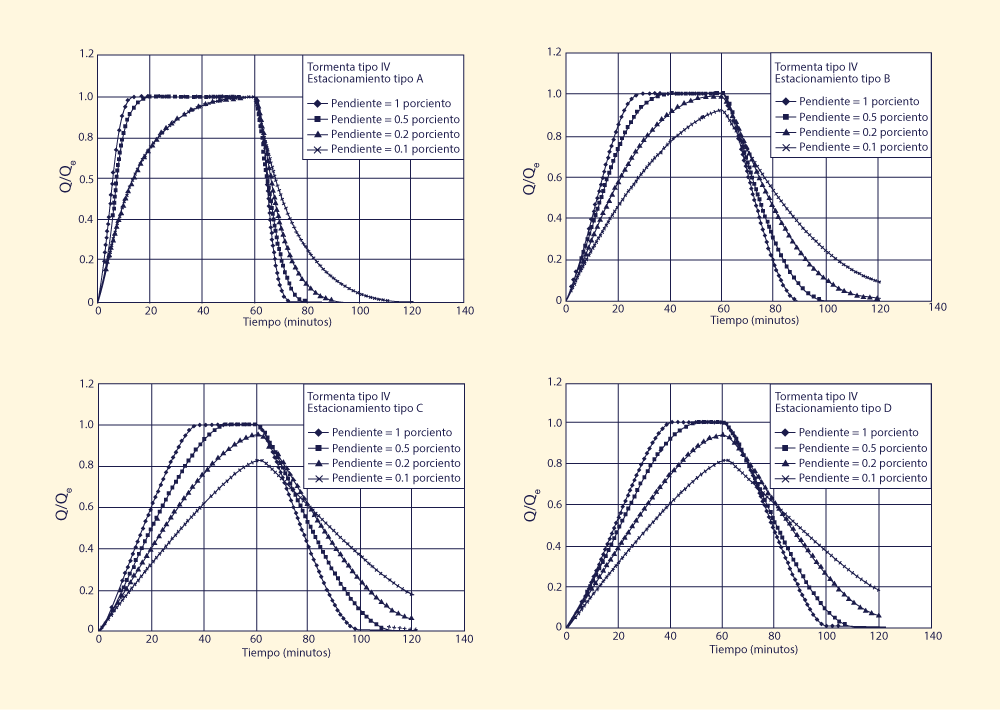
Las Figuras 1-4 muestran los resultados de la simulación. Para cada tipo de tormenta, cuatro tipos de áreas de estacionamiento y cuatro pendientes de diseño dieron lugar a dieciséis (16) simulaciones. Las descargas mostradas son descargas normalizadas, es decir, las descargas de flujo de salida Q divididas por su respectivo flujo de salida de equilibrio Q_e (Tabla 2).

Fig. 1  Hidrogramas de salida para la tormenta tipo Ι.

Fig. 2  Hidrogramas de salida para la tormenta tipo ΙΙ.

Fig. 3  Hidrogramas de salida para la tormenta tipo ΙΙΙ.

Fig. 4  Hidrogramas de salida para la tormenta tipo ΙV.

El análisis de las Figs. 1-4 conduce a las siguientes conclusiones:

1. A medida que la pendiente disminuye de 1 a 0.1%, la tasa de aumento del hidrograma de salida disminuye. Esto retrasa el logro del flujo de salida en equilibrio, aumentando el tiempo de concentración de cinemático a difusivo, y extendiendo en el tiempo el hidrograma de salida [ver, por ejemplo, las Figs. 3(d) y 4(d)].

2. Para una duración de tormenta menor que el tiempo de concentración difusivo, el retraso en el logro del flujo de salida en equilibrio produce un flujo subconcentrado (Ponce 1989) y da como resultado un efectivo comportamiento difusivo [Figs. 3(c) y 4(c)].

3. Para las tormentas más cortas (5 y 15 min), el flujo de salida de equilibrio no se alcanza en la mayoría de los casos. La extensión en el tiempo del hidrograma de salida da como resultado un efectivo comportamiento difusivo [véanse, por ejemplo, las Figs. 1(c) y 2(c)].

4. Para tormentas más largas (30 y 60 min), el flujo de salida de equilibrio se alcanza en la mayoría de los casos. Sin embargo, el retraso da como resultado la extensión en el tiempo del hidrograma de flujo de salida, es decir, en un efectivo comportamiento difusivo [Figs. 3(b) y 4(b)].

4.  RESUMEN

Se utiliza un modelo de onda difusiva para la dinámica de las cuencas con el fin de evaluar la viabilidad de utilizar la pendiente como parámetro de diseño en la gestión del drenaje urbano. El almacenamiento en las área de estacionamiento se define como la estrategia para detener temporalmente la escorrentía de las tormentas en los estacionamientos para proporcionar una cantidad apreciable de retención de aguas pluviales en lugar de un drenaje rápido e inmediato.

La prueba incluyó un caso cinemático (pendiente del 1%) y tres casos difusivos (pendientes del 0.5, 0.2 y 0.1%). Los resultados del modelo muestran que cuanto menor es la pendiente, más lenta es la velocidad de crecimiento del hidrograma de salida. Esto retrasa el logro del flujo de salida de equilibrio, lo que resulta en flujos máximos más bajos y/o una base de tiempo más larga, es decir, en un efectivo comportamiento difusivo. Por lo tanto, el área de estacionamiento puede proporcionar una cantidad apreciable de almacenamiento de agua de lluvia si está diseñada específicamente para este propósito.

APÉNDICE.  BIBLIOGRAFÍA

Architectural graphic standards design manual. 1988. Ramsey/Sleeper, The American Institute of Architects, Wiley, New York.

Chow, V. T. 1959. Open channel hydraulics. McGraw-Hill, New York.

Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum method)." J. Hydr. Res., Delft, The Netherlands, 7(2), 205-230.

Dooge, J. C. I. 1973. "Linear theory of hydrologic systems." Tech. Bull. 1468, USDA, Washingon, D.C.

Dooge, J. C. I., W. B. Strupezewski, y J. J. Napiorkowski, J. J. 1982. "Hydrodynamic derivation of storage parameters of the Muskingum model." J. Hydro., Amsterdam, 54, 371-387.

"Flood studies report." 1975. Flood routing studies, Vol. ΙΙΙ, Natural Environment Research Council, London.

Hayami, S. 1951. "On the propagation of flood waves." Bull. Disaster Prevention Res. Inst., Vol. 1, Kyoto University, Kyoto, Japan, 1-16.

HEC-1, flood hydrograph package: User's manuanl. 1990. U.S. Army Corps of Engineers, Hydrologic Engineering Center, Davis, Calif.

Hjelmfelt, A. T. Jr. 1985. "Negative outflows from Muskingum flood routing." J. Hydr. Engrg., ASCE, 111(6), 1010-1014.

Orlandini, S., and Rosso, R. 1996. "Diffusion wave modling of distributed catchment dynamics." J. Hydr. Engrg., ASCE, 1(3), 103-113.

Ponce, V. M. 1986. "Diffusion wave modeling of catchment dynamics." J. Hydr. Engrg., ASCE, 112(8), 716-727.

Ponce, V. M. 1989. Engineering hydrology, principles and practices. Prentice-Hall, Englewood Cliffs, N.J.

Ponce, V. M. 1991. "New perspective on the Vedernikov number." Water Resour. Res., 27(7), 1777-1779.

"Rainfall depth-duration-frequency for California." 1982. Dept. of Water Resour., Div. of Plng., The Resources Agency, Calif.

Seddon, J. A. 1990. "River hydraulics." Trans. ASCE, 43, 179-243.

Stahre, P., y Urbonas, B. 1990. Stormwater detention for drainage, water quality, and CSO management. Prentice-Hall, Englewood Cliffs, N.J.

Vedernikov, V. V. 1945. "Conditions at the front of a translation wave disturbing a steady motion of a real fluid." USSR Acad. Sciences Comptes Rendus (Doklady), Moscow, 48(4), 239-242.

Wooding, R. A. 1965. "A hydraulic model for the catchment-stream problem." J. Hydro., Amsterdam, 3, 254-267.