1.  INTRODUCCIÓN

En el artículo complementario (Ponce y Shetty, 1995) se ha descrito un modelo conceptual del balance hídrico que separa la precipitación anual en escorrentía superficial y humectancia, y esta última en flujo base y vaporización, siguiendo los conceptos sugeridos por L'vovich (1979). El objetivo es determinar la fracción de precipitación anual que entra en la escorrentía superficial, y la fracción de humectancia que entra en el flujo base. La escorrentía consiste de escorrentía superficial y flujo base. Existe una competencia entre la escorrentía superficial y la humectancia. Cualquier gota de agua que entra en la escorrentía superficial es una gota que no se suma a la humectancia. De manera similar, existe una competencia entre el flujo base y la vaporización. Cualquier gota de agua que ingrese al flujo base es una gota que no deja la cuenca por vaporización.

Al respecto de esta competencia, la evidencia se muestra dispersa en la literatura. A nivel mundial, las diferencias en regiones biogeográficas y entornos climáticos han tendido a enmascarar la naturaleza de la competencia. Por ejemplo, Pitman (1978) ha documentado la disminución del caudal de los arroyos después de la reforestación a gran escala en SudÁfrica. Baker (1986) ha informado de aumentos temporales en el caudal de los arroyos después del tratamiento con herbicidas en una cuenca de piñones y enebros en el centro-norte de Arizona. Ruprecht y Schofield (1989) han documentado aumentos tanto en la escorrentía superficial como en el flujo base luego del reemplazo de especies forestales nativas de raíces profundas por especies agrícolas de raíces poco profundas en Australia Occidental. Sin embargo, Ruprecht y Stoneman (1993) han declarado que el pronóstico a largo plazo para el rendimiento anual de agua de las áreas sujetas a aprovechamiento forestal en Australia Occidental es incierto. Hibbert (1967) matizó su revisión de los experimentos de cuencas para aumentar el rendimiento de agua al afirmar que la respuesta de las cuencas al tratamiento era muy variable y, en su mayor parte, impredecible. Sin embargo, Bosch y Hewlett (1982), en su revisión exhaustiva de los experimentos en cuencas para aumentar el rendimiento de escorrentía, no se inclinaron a apoyar las dudas de Hibbert. El tema de la competencia entre la escorrentía (incluido el flujo base) y la vaporización es de gran interés práctico, ya que la disminución de la escorrentía se asocia invariablemente con la disminución de los recursos hídricos.

En este artículo se simula la escorrentía y el flujo base utilizando un modelo conceptual de balance hídrico descrito en el artículo complementario (Ponce and Shetty, 1995). La base conceptual del modelo mejora su aplicabilidad a una amplia gama de regiones biogeográficas y entornos climáticos. Los datos seleccionados de las cuencas de África, América del Norte y América del Sur (L'vovich, 1979) se complementan con los propios datos de los autores, provenientes de Asia. Se derivan dos funciones de escorrentía y flujo base: (1) coeficientes de escorrentía y flujo base en función de la precipitación anual; (2) ganancia de escorrentía y flujo base en función de la precipitación anual. El análisis de estas funciones conduce a una caracterización de la escorrentía y flujo base a través del espectro climático, arrojando luz adicional sobre la competencia entre escorrentía y vaporización, y flujo base y vaporización.

2.  MODELO CONCEPTUAL

La precipitación anual P se puede dividir en dos componentes (Ponce y Shetty, 1995):

P = S + W

(1)

en la cual S = escorrentía superficial y W = humectancia. A su vez, la humectancia se divide en dos componentes:

W = U + V

(2)

en la cual U = flujo base y V = vaporización. El término "vaporización" abarca toda la humedad devuelta a la atmósfera por evaporación: evapotranspiración de áreas con vegetación, evaporación de áreas sin vegetación, y evaporación de cuerpos de agua.

La escorrentía consiste en la escorrentía superficial y el flujo base:

R = S + U

(3)

Combinando las Ecs. 1 y 3 se obtiene:

P = R + V

(4)

El coeficiente de escorrentía es:

R Kr  =  ____            P

(5)

El coeficiente de vaporización es:

V Kv = ____ = 1 - Kr           P

(6)

La ganancia de escorrentía se define como sigue:

dKr K'r = ______           dP

(7)

La pérdida por vaporización es la derivada del coeficiente de vaporización, o también:

K'v = - K'r

(8)

El coeficiente del flujo base es (L' vovich, 1979)

U Ku = ____          W

(9)

La ganancia de flujo base se define como sigue:

dKu K'u = _____            dP

(10)

La separación secuencial de la precipitación anual en escorrentía superficial y humectancia, y esta última en flujo base y vaporización, se modela mediante una relación proporcional de tal manera que la humectancia alcanza asintóticamente un límite superior a medida que la precipitación y la escorrentía superficial aumentan sin límites. Asimismo, la vaporización alcanza asintóticamente un límite superior a medida que la humectancia y el flujo base aumentan sin límites. Los submodelos de escorrentía superficial y flujo base están dadas en las Ecs. 16 y 18 respectivamente, del artículo complementario (Ponce y Shetty, 1995).

Dado un conjunto de parámetros del modelo λ_s, W_p, λ_u y V_p, el modelo conceptual separa la precipitación anual en escorrentía superficial y humectancia, y esta última en flujo base y vaporización. El procedimiento se puede aplicar a un rango realista de precipitación anual, del cual se derivan las funciones de escorrentía y flujo base (Ecs. 5, 7, 9 y 10).

3.  APLICACIÓN DEL MODELO

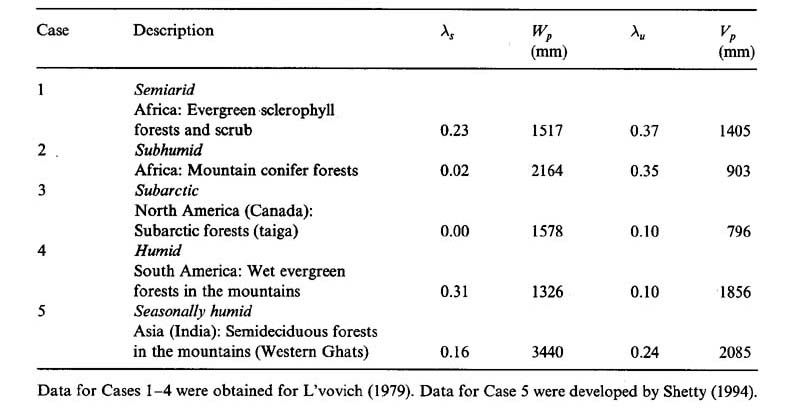
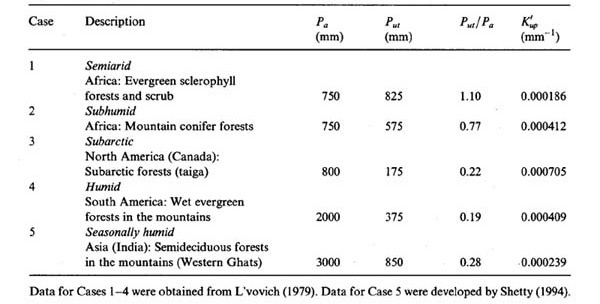
La Tabla 1 muestra los parámetros del modelo, calibrado para cinco casos. Los primeros cuatro casos se incluyeron en el artículo complementario (Ponce y Shetty, 1995). En esta contribución, agregamos un quinto caso: la cuenca del río Malaprabha, en Khanapur, Karnataka (India), que consiste principalmente en bosques semideciduos en las laderas orientales de los Ghats Occidentales (Shetty, 1994). La cuenca de Malaprabha tiene un clima estacionalmente húmedo, caracterizado por lluvias impulsadas por vientos monzones, los cuales duran de 4 a 5 meses. Los cinco casos seleccionados abarcan una amplia gama de entornos climáticos, como sigue: Caso 1: Semiárido; Caso 2: Subhúmedo; Caso 3: Subártico; Caso 4: Húmedo; Caso 5: Estacionalmente húmedo.

Tabla 1.  Parámetros del modelo conceptual para los casos seleccionados.

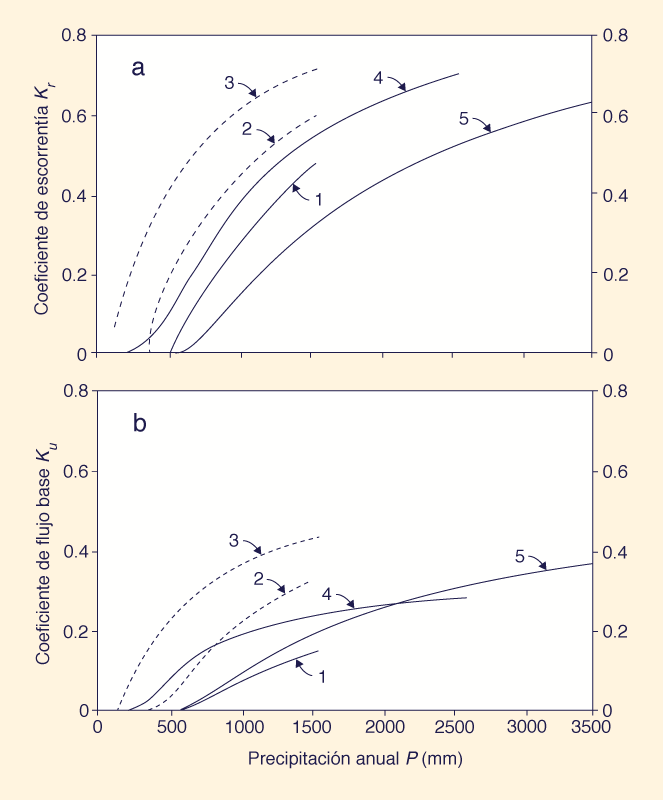
La Figura 1 muestra los coeficientes de escorrentía y flujo base para los cinco casos incluidos en este artículo. El análisis de esta figura conduce a las siguientes conclusiones:

1. Los coeficientes de escorrentía y flujo base aumentan monotónicamente con la precipitación anual, comenzando desde cero en la mayoría de los casos. Cuanto más seco sea el clima y menor sea la precipitación anual, mayor será la probabilidad de que los coeficientes comiencen desde cero.

2. Los coeficientes de escorrentía y flujo base aumentan notablemente para los valores de precipitación anual en el rango bajo y medio.

3. Los coeficientes de escorrentía y flujo base tienden a alcanzar un límite superior para valores de precipitación anual en el rango alto y muy alto.

Fig. 1. Coeficientes de escorrentía y flujo base para los cinco casos tratados en este estudio.

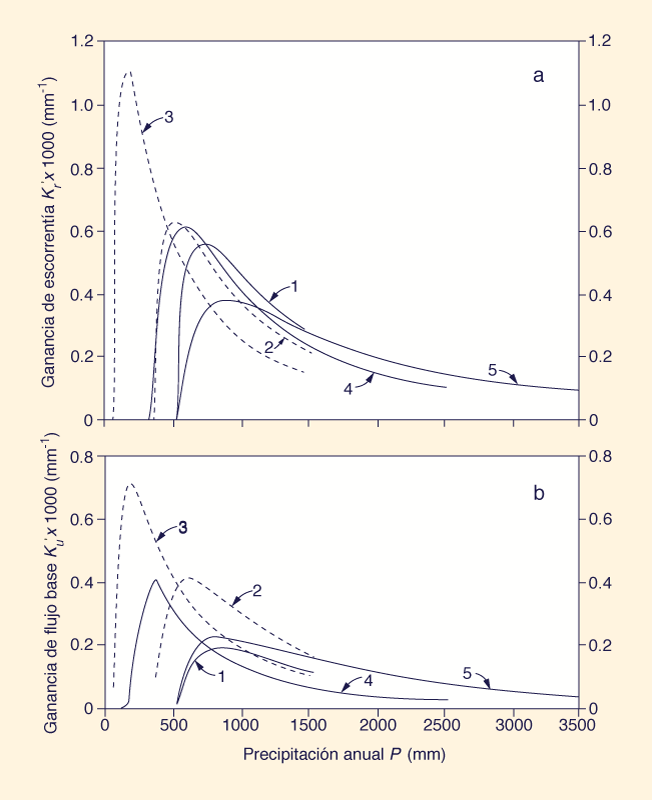
La Figura 2 muestra el aumento de escorrentía y flujo base para los cinco casos tratados en este estudio. El análisis de esta figura conduce a las siguientes conclusiones:

1. La ganancia de escorrentía es siempre positiva, alcanzando un pico K'_rp en un umbral de precipitación de escorrentía P_rt.

2. La ganancia de flujo base es siempre positiva, alcanzando un pico K'_up en un umbral de precipitación de flujo base P_ut.

3. Un incremento/disminución en la ganancia de escorrentía o flujo base corresponde a una disminución/incremento en la ganancia de vaporización, es decir, un aumento/disminución en la pérdida por vaporización.

Fig. 2.  Coeficientes de escorrentía y flujo base para los cinco casos tratados en este estudio.

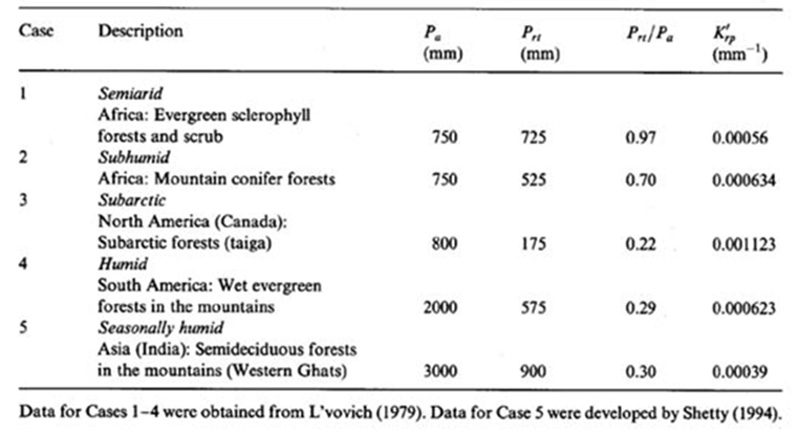
La Tabla 2 muestra la precipitación media anual, el umbral de precipitación de escorrentía, la relación entre el umbral de precipitación de escorrentía y la precipitación anual media y la ganancia máxima de escorrentía para los cinco casos tratados en este estudio. El análisis de esta tabla conduce a las siguientes conclusiones:

1. El umbral de precipitación de escorrentía varía con el entorno climático de la siguiente manera: (a) en regiones semiáridas y estacionalmente húmedas, P_rt es alto (725-900 mm); (b) en regiones subhúmedas y húmedas, P_rt tiene valores de rango medio (525-575 mm); y (c) en las regiones subárticas, P_rt es bajo (175 mm).

2. La ganancia pico de escorrentía varía con el entorno climático, como sigue: (a) en regiones estacionalmente húmedas, K'_rp es bajo (0.00039 mm^-1); (b) en regiones semiáridas, subhúmedas y húmedas, K'_rp tiene valores de rango medio (0.00056-0.000634 mm^-1); y (c) en regiones subárticas, K'_rp es alto (0.001123 mm^-1).

3. La relación entre el umbral de precipitación de escorrentía y la precipitación media anual caracteriza el entorno climático de la siguiente manera: (a) en las regiones semiáridas, el valor P_rt ∕P_a, es alto, cerca de la unidad; por ejemplo, el valor de los bosques y matorrales esclerófilos de hoja perennifolíos en África es de 0.97; (b) en regiones subhúmedas, P_rt ∕P_a tiene valores de rango medio, menores que la unidad; el valor de los bosques de coníferas de montaña en África es de 0.70; (c) en regiones estacionalmente húmedas, húmedas y subárticas, P_rt ∕P_a tiene valores bajos, típicamente menores o iguales a 0.3; los valores medidos para Asia, Sudamérica y Norteamérica oscilan entre 0.22 y 0.30.

Tabla 2.  Precipitación media anual Pa, umbral de precipitación de escorrentía Prt, relación Prt ∕ Pa y ganancia máxima de escorrentía K'rp para casos seleccionados.

La Tabla 3 muestra la precipitación media anual, el umbral de precipitación de flujo base, la relación entre el umbral de precipitación de flujo base y la precipitación media anual y la ganancia pico de flujo base para los cinco casos tratados en este artículo. El análisis de esta tabla conduce a las siguientes conclusiones:

1. El umbral de precipitación de flujo base varía con el entorno climático, como sigue: (a) en regiones semiáridas y estacionalmente húmedas, P_ut es alto (825-850 mm); (b) en regiones subhúmedas y húmedas, P_ut tiene valores de rango medios (370-575 mm); y (c) en las regiones subárticas, P_ut es bajo (175 mm).

2. La ganancia pico de flujo base varía con el entorno climático, como sigue: (a) en regiones semiáridas y estacionalmente húmedas, K'_up es bajo (0.000186-0.000239 mm^-1); (b) en regiones subhúmedas y húmedas, K'_up tiene valores de rango medio (0.000409 - 0.000412 mm^-1); y (c) en las regiones subárticas, K'_up es alto (0.000705 mm^-1).

3. La relación entre el umbral de precipitación del flujo base y la precipitación media anual caracteriza el entorno climático, de la siguiente manera: (a) en las regiones semiáridas, el valor P_ut ∕P_a es alto, cercano a la unidad; por ejemplo, el valor de los bosques y matorrales esclerófilos perennifolíos en África es de 1.10; (b) en regiones subhúmedas, P_ut ∕P_a tiene valores de rango medio, menores que la unidad; el valor de los bosques de coníferas de montaña en África es 0.77; y (c) en regiones estacionalmente húmedas, húmedas y subárticas, P_ut ∕P_a tiene valores bajos típicamente inferiores a 0.3; los valores medidos para Asia, Sudamérica y Norteamérica oscilan entre 0.19 a 0.28.

Tabla 3. Precipitación media anual Pa, umbral de precipitación de flujo base Put, relación Put /Pa y ganancia pico de flujo base pico K'up para los casos seleccionados.

4.  COMPETENCIA ENTRE ESCORRENTÍA Y VAPORIZACIÓN, Y ESCORRENTÍA Y FLUJO BASE

El análisis de la función de ganancia de escorrentía sirve para aclarar la naturaleza de la competencia entre escorrentía y vaporización. Son dos los posibles escenarios, dependiendo de la magnitud de la precipitación anual en relación con el umbral de precipitación de escorrentía (P_rt ): (1) para P < P_rt , los aumentos en la precipitación anual conducen a aumentos en la ganancia de escorrentía y aumentos proporcionalmente mayores en la escorrentía; (2) para P > P_rt , los aumentos en la precipitación anual conducen a disminuciones en la ganancia de escorrentía y aumentos proporcionalmente menores en la escorrentía.

Para regiones semiáridas P_rt/P_a ≈ 1. Por lo tanto: (1) P < P_rt implica que P < P_a , y P > P_rt implica que P > P_a . Concluimos que la escorrentía es un fuerte competidor sobre la vaporización en el caso de mayor interés práctico, es decir, en regiones semiáridas cuando la precipitación anual está por debajo del promedio. Es decir, en una región semiárida, es más probable que una gota de lluvia se convierta en escorrentía en el lado seco del espectro de lluvia anual (P < P_a ). Por el contrario, es más probable que una gota de lluvia se vaporice en el lado húmedo del espectro de lluvia anual (P > P_a ).

A diferencia de las regiones semiáridas, para regiones estacionalmente húmedas, húmedas y subárticas P_rt ∕ P_a < 0.3. Por lo tanto: (1) P < P_rt implica que P < 0.3 P_a , y (2) P > P_rt implica que P > 0.30 P_a . Concluimos que la vaporización es un fuerte competidor de la escorrentía en las regiones húmedas (incluidas las estacionalmente húmedas y subárticas) cuando la precipitación anual está por encima de 0.3 P_a . Es decir, en una región húmeda, es más probable que una gota de lluvia se vaporice en un amplio rango de variación de la precipitación anual (P > 0.3 P_a).

La competencia entre el flujo base y la vaporización sigue un patrón similar al de la escorrentía y la vaporización. En las regiones semiáridas, el flujo base es un fuerte competidor de la vaporización en el lado seco del espectro de lluvia anual (P < P_a). En regiones húmedas, la vaporización prevalece sobre el flujo base en un amplio rango de variación de la precipitación anual (P > 0.3 P_a).

4.  RESUMEN

Se utiliza un modelo conceptual de balance hídrico para simular cambios en la escorrentía y el flujo base con la precipitación anual. El modelo se basa en la separación secuencial de la precipitación anual en escorrentía superficial y humectancia, y esta última en flujo base y vaporización. La separación está modelada por una relación proporcional de tal manera que la humectancia alcanza asintóticamente un límite superior a medida que la precipitación y la escorrentía superficial aumentan sin límites. Asimismo, la vaporización alcanza asintóticamente un límite superior a medida que la humectancia y el flujo base aumentan sin límites. Los parámetros del modelo son el coeficiente de abstracción inicial para la escorrentía superficial λ_s, el potencial de humectancia W_p, el coeficiente de abstracción inicial para el flujo base λ_u, y el potencial de vaporización V_p.

La ganancia de escorrentía se define como la derivada del coeficiente de escorrentía con respecto a la precipitación. La ganancia de flujo base se define como la derivada del coeficiente de flujo base con respecto a la precipitación. Los datos muestran que las ganancias de flujo base son siempre positivas. La ganancia de escorrentía alcanza un pico para un umbral de precipitación de escorrentía; la ganancia de flujo base alcanza un pico para un umbral de precipitación de flujo base.

Se derivan dos funciones de escorrentía y flujo base: (1) coeficientes de escorrentía y flujo base versus precipitación anual; (2) ganancias de escorrentía y flujo base versus precipitación anual. Se muestra la relación del umbral de precipitación P_t a la precipitación media anual P_a, para caracterizar el entorno climático de la siguiente manera: en regiones semiáridas, P_t ∕P_a es alto, con valores cercanos a la unidad; en regiones subhúmedas, P_t∕P_a tiene valores de rango medio, menores que la unidad; en regiones estacionalmente húmedas, húmedas y subárticas, P_t∕P_a tiene valores bajos, generalmente menores o iguales a 0.3.

El análisis de las funciones de escorrentía y flujo base arroja luz adicional sobre la naturaleza de la competencia entre escorrentía y vaporización, y flujo base y vaporización. Se ha demostrado que la escorrentía y el flujo base son fuertes competidores sobre la vaporización en el caso de mayor interés práctico, es decir, en regiones semiáridas cuando la precipitación anual está por debajo del promedio (P < P_a ). Por otro lado, se ha demostrado que la vaporización es un fuerte competidor de la escorrentía y el flujo base en regiones húmedas a través de un amplio rango de variación de la precipitación anual (P > 0.3 P_a).

AGRADECIMIENTOS

El presente estudio se realizó en la primavera de 1994, mientras que A. V. Shetty estaba realizando una estancia en la Universidad Estatal de San Diego, con licencia del Centro Regional Hard Rock, Instituto Nacional de Hidrología, Belgaum, Karnataka, India. Su licencia fue financiada por el Programa de las Naciones Unidas para el Desarrollo.

 BIBLIOGRAFÍA

1. Baker, Jr., M. B., 1986. Effects of Ponderosa pine treatment on water yield in Arizona. Water Resour. Res., 22(1): 63-67.

2. Bosch, J. M. y Hewlett, J. D., 1982. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol., 55: 3-23.

3. Hibbert, A. R., 1967. Forest treatment effects on water yield. In: W.E. Sopper and H.W. Lull (Editors), International Symposium on Forest Hydrology. Pergarnon, Oxford.

4. L'vovich, M. I., 1979. World water resources and their future. Original in Russian. English translation, American Geophysical Union, Washington, DC.

5. Pitman, W. V., 1978. Trends in streamflow due to upstream land use changes. J. Hydrol., 39:227-237. .

6. Ponce, V. M. y Shetty, A. V., 1995. A conceptual model of catchment water balance: 1. Formulation and calibration. J. Hydrol., 173: 27-40.

7. Ruprecht, J. K. y Schofield, N. J., 1989. Analysis of streamflow generation following deforestation in southwest Western Australia. J. Hydrol., 105: 1-17

8. Ruprecht, J. K. y Stoneman, G. L., 1993. Water yield issues in the jarrah forest of southwestern Australia. J. Hydrol., 150: 369-391.

9. Shetty. A. V. 1994. Application of water balance conceptual model to the Malaprabha river basin, Karnataka. National Institute of Hydrology Report, Roorkee, Roorkee, Uttar Pradesh, India.