|
1. INTRODUCTION Urban development decreases surface roughness and infiltration rates, thus decreasing the time of concentration and increasing surface runoff. When taken in the aggregate, these effects result in an increase in the magitude and frequency of floods at downstream sites, at any scale. To counter this trend, runoff detention and retention is now being seen as an alternative strategy (Stahre and Urbonas 1990). The rationale behind this change of approach is the recognition that the conventional drainage strategy has its pitfalls: While it effectively reduces the local flooding risk, it results in an increase in the regional flooding risk. Herein we define "kinematic drainage" as the strategy that produces a storm hydrograph rising at the fastest possible rate. "Diffusive drainage," on the other hand, is that which produces a storm hydrograph rising at rates lower than kinematic. The calculation of diffusive drainage is possible with the diffusion wave model of catchment dynamics (Ponce 1986; Orlandini and Rosso 1996). The diffusion effect reduces the rate-of-rise of the outflow hydrograph, increasing the time base, spreading the flow in time, and reducing the flood risk downstream.
In this note, we use the diffusion wave model to quantify runoff detention in parking lots. 2. DIFFUSION WAVE MODEL The diffusion wave model used herein is an extension of the Muskingum-Cunge method of flood routing (Cunge 1969; "Flood" 1975) to overland flow phenomena (Ponce 1986). The geometric configuration follows Wooding's (1965) open book. The input to the planes is effective rainfall intensity, which is converted to lateral inflow into the center channel draining the two planes. In turn, the lateral inflow is routed to the outlet and expressed as an outflow hydrograph. Because its hydraulic diffusivity is a function of the Vedernikov number (Vedernikov 1945; Chow 1959), the catchment model has a significant dynamic component (Dooge 1973; Dooge et al. 1982; Ponce 1991). Thus, diffusion vanishes if the Vedernikov number approaches one. However, under the flow conditions normally encountered in overland flow, the Vedernikov number is usually well below one.
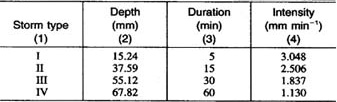
The Muskingum-Cunge method works by matching physical and numerical diffusivities. Unlike the kinematic wave model, which is a one-parameter model, and therefore, responsive only to wave celerity (Seddon 1900; Chow 1959), the diffusion wave model is a two-parameter model and is responsive to both wave celerity and hydraulic diffusivity (Hayami 1951). In essence, this means that the diffusion wave model can simulate a perceptible hydrograph feature such as flow spreading, which is directly traceable to the hydraulic diffusivity. On the other hand, a comparable kinematic wave model is unable to effectively account for the flow diffusivity, resulting in simulations that are dependent on grid size (Ponce 1986). Because the hydraulic diffusivity is inversely related to plane and channel slope, the diffusion wave model is suited to applications where slope plays a major role. The steeper the slope, the more kinematic and less diffusive the flow is; conversely, the milder the slope, the more diffusive and less kinmeatic the flow is. For a sufficiently steep slope, the flow becomes kinematic and the resulting outflow hydroraph rises at the fastest possible rate. For the milder slopes, the outflow hydrograph rises at rates lower than kinematic. The above reasoning led to the formulation of a testing program designed to determine the sensitivity of overland flow hydrographs to plane and channel slope. The aim is to assess the feasibility of using slope as a design parameter in urban storm water management. 3. TESTING PROGRAM AND MODEL RESULTS The testing program was designed to vary storm intensity, catchment area, and design slope for a wide range of conditions. Four extreme storm types shown in Table 1 were established fo the San Diego urban area ( "Rainfall" 1982 ).
Four typical parking lot sizes were selected, ranging from 0.105 to 6.88 ha (Architectural 1988).
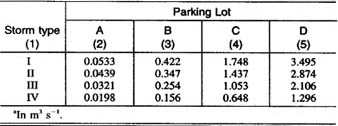
Equilibrium outflows for each storm and parking lot type are shown in Table 2 (Ponce 1989).
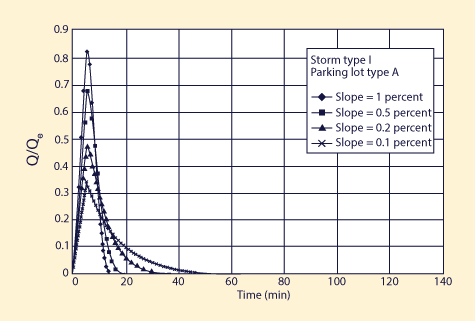
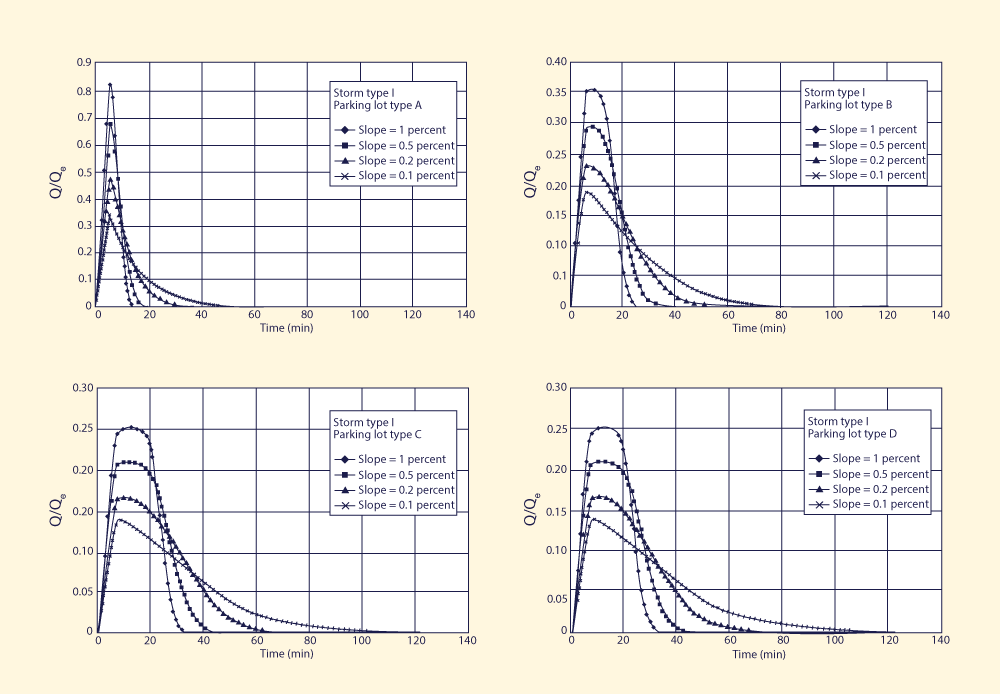
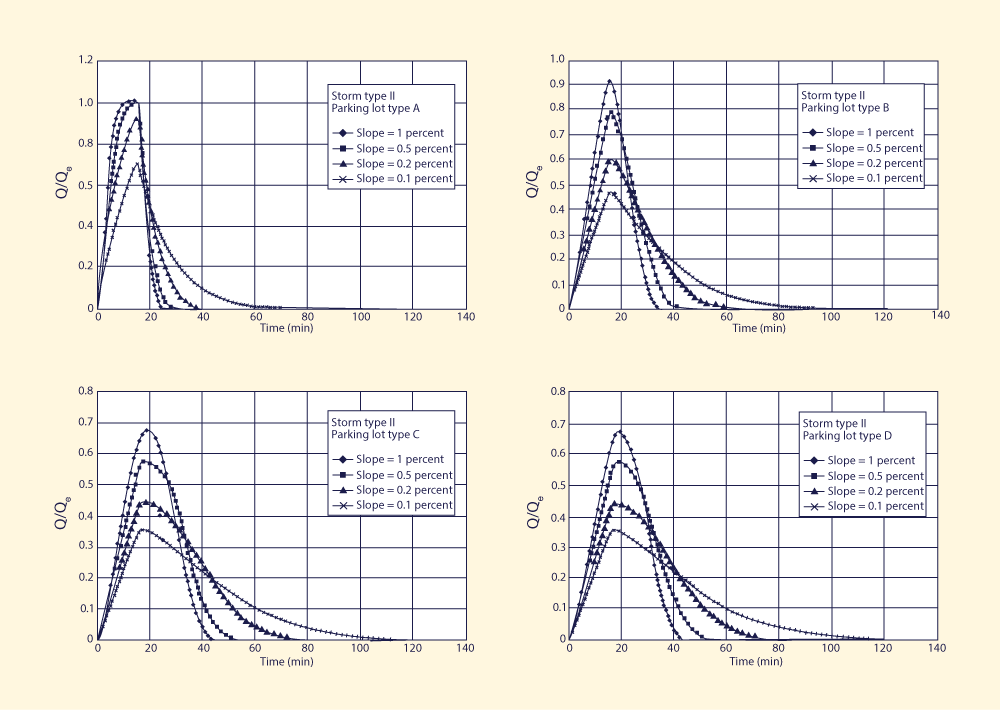
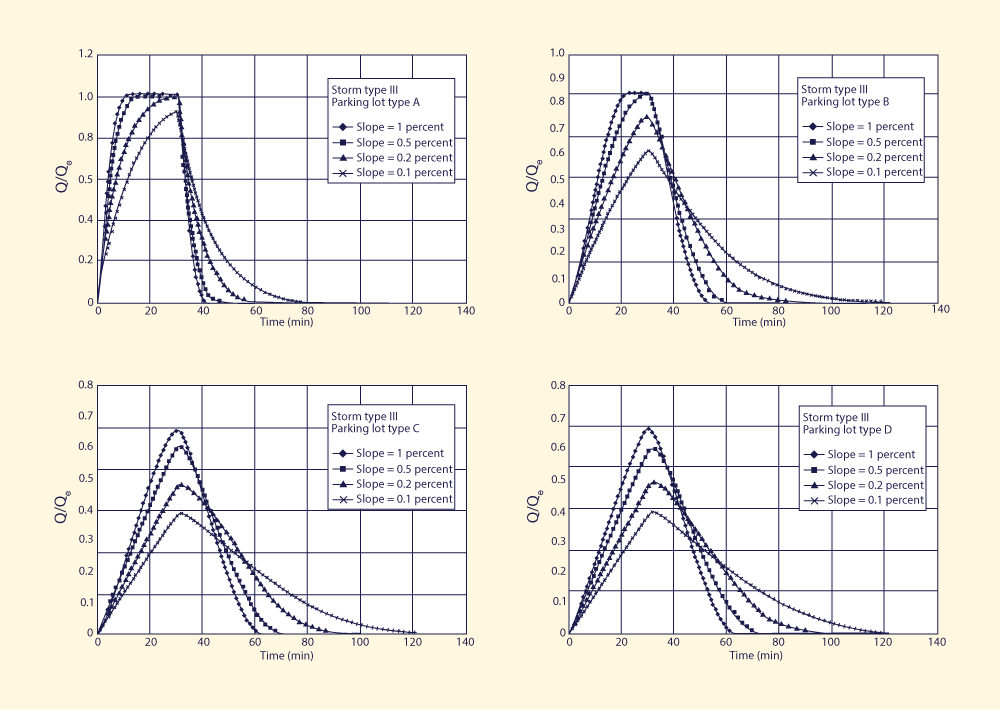
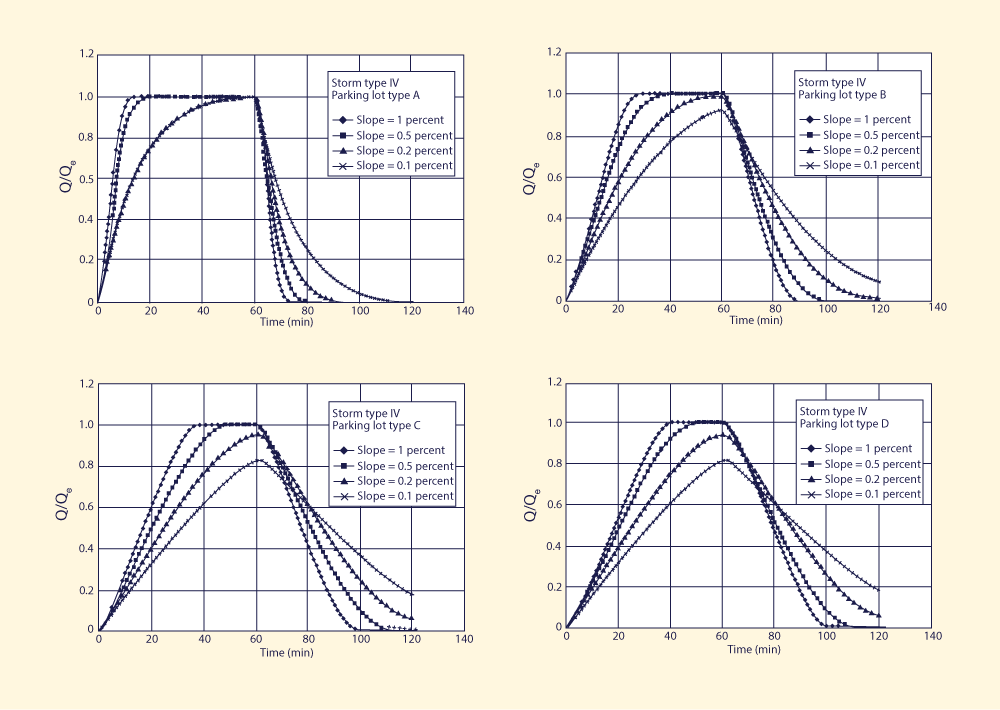
Four design slopes were chosen to reflect a wide range of flow conditions, from kinematic to diffusive. Slopes less than 0.1 percent were judged to be impractical due to the possibility of excessive ponding, which could impair drivability. The selected slopes were: (1) 1 percent, kinematic; (2) 0.5 percent, mildly diffusive; (3) 0.2 percent, moderately diffusive; and (4) 0.1 percent, strongly diffusive. Figures 1-4 show the results of the simulation. For each storm type, four parking lot types and four design slopes led to: 4 × 4 = 16 runs. The discharges shown are normalized discharges, i.e., the outflow discharges Q divided by their respective equilibrium outflow Qe (Table 2).
Analysis of Figs. 1-4 leads to the following conclusions:
4. SUMMARY A diffusion wave model of catchment dynamics is used to assess the feasibility of using slope as a design parameter in urban storm water management. Parking lot storage is defined as the strategy to temporarily detain storm runoff in parking lots to provide an appreciable amount of storm water detention instead of fast and immediate drainage. The testing included one kinematic case (1 percent slope) and three diffusive cases (0.5, 0.2, and 0.1 percent slopes). Model results show that the smaller the slope, the slower the rate-of-rise of the outflow hydrograph. This delays the attainment of equilibrium outflow, resulting in lower peak flows and/or longer time base, i.e., in an effective diffusive behavior. Thus, a parking lot can provide a substantial amount of storm water storage if it is specifically designed for this purpose. APPENDIX. REFERENCES
Architectural graphic standards design manual. 1988. Ramsey/Sleeper, The American Institute of Architects, Wiley, New York.
Chow, V. T. 1959. Open channel hydraulics. McGraw-Hill, New York.
Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum method)." J. Hydr. Res., Delft, The Netherlands, 7(2), 205-230.
Dooge, J. C. I. 1973. "Linear theory of hydrologic systems." Tech. Bull. 1468, USDA, Washingon, D.C.
Dooge, J. C. I., W. B. Strupzewski, and J. J. Napiorkowski. 1982. "Hydrodynamic derivation of storage parameters of the Muskingum model." J. Hydro., Amsterdam, 54, 371-387.
"Flood studies report." 1975. Flood routing studies, Vol. ΙΙΙ, Natural Environment Research Council, London.
Hayami, S. 1951. "On the propagation of flood waves." Bull. Disaster Prevention Res. Inst., Vol. 1, Kyoto University, Kyoto, Japan, 1-16.
HEC-1, flood hydrograph package: User's manuanl. (1990). U.S. Army Corps of Engineers, Hydrologic Engineering Center, Davis, Calif.
Hjelmfelt, A. T. Jr. 1985. "Negative outflows from Muskingum flood routing." J. Hydr. Engrg., ASCE, 111(6), 1010-1014.
Orlandini, S., and R. Rosso. 1996. "Diffusion wave modeling of distributed catchment dynamics." J. Hydr. Engrg., ASCE, 1(3), 103-113.
Ponce, V. M. 1986. "Diffusion wave modeling of catchment dynamics." J. Hydr. Engrg., ASCE, 112(8), 716-727.
Ponce, V. M. 1989. Engineering hydrology, principles and practices. Prentice-Hall, Englewood Cliffs, N.J.
Ponce, V. M. 1991. "New perspective on the Vedernikov number." Water Resour. Res., 27(7), 1777-1779.
"Rainfall depth-duration-frequency for California." 1982. Dept. of Water Resour., Div. of Plng., The Resources Agency, Calif.
Seddon, J. A. 1900. "River hydraulics." Trans. ASCE, 43, 179-243.
Stahre, P., and B. Urbonas. 1990. Stormwater detention for drainage, water quality, and CSO management. Prentice-Hall, Englewood Cliffs, N.J.
Vedernikov, V. V. 1945. "Conditions at the front of a translation wave disturbing a steady motion of a real fluid." USSR Acad. Sciences Comptes Rendus (Doklady), Moscow, 48(4), 239-242.
Wooding, R. A. 1965. "A hydraulic model for the catchment-stream problem." J. Hydro., Amsterdam, 3, 254-267.
|
| 230214 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |