1. PENMAN MODEL The original Penman model is a combination method in which the total evaporation rate is calculated by weighing the evaporation rate due to net radiation and the evaporation rate due to mass transfer, as follows (Ponce, 1989):
in which E = total evaporation rate; En = evaporation rate due to net radiation; Ea = evaporation rate due to mass transfer; Δ = saturation vapor pressure gradient, a function of air temperature; and γ = psychrometric constant, which may be shown to vary slightly with temperature. The mass-transfer evaporation rate Ea is calculated with an empirical mass-transfer formula. 2. PENMAN-MONTEITH MODEL In the Penman-Monteith method, the mass-transfer evaporation rate Ea is calculated based on physical principles. The original form of the Penman-Monteith equation, in dimensionally consistent units, is:
in which
The quantity ra-1 is the external conductance, in cm3 of air per cm2 of surface per second (cm/s).
In evaporation rate units, Eq. 2 is expressed as follows:
in which
Equation 4 is the Penman-Monteith model of evaporation. 3. PHYSICAL CONSTANTS The density of dry air at 0°C and sea-level atmospheric pressure is: ρad = 1.2929 kg/m3. The density of moist air ρa may be approximated as follows:
in which T = air temperature, in °C. For instance, at T = 20°C and sea level (standard atmospheric pressure): ρa = 0.0012046 gr/cm3. The specific heat of moist air, in the range 0°C ≤ T ≤ 40°C, is: cp = 1.005 J/(gr-°C) Converting to calories: cp = (1.005 J/(gr-°C) (0.239 cal/J) = 0.2402 cal/(gr-°C). 4. DAILY EVAPORATION RATE In evaporation units of cm/d, Eq. 4 is expressed as follows:
in which
Equation 6 can be conveniently expressed in Penman form (Eq. 1) as follows:
in which Ea = evaporation rate due to mass transfer, in cm/d. 5. EVAPORATION RATE DUE TO MASS TRANSFER Comparing Eqs. 6 and 7, the evaporation rate due to mass transfer is obtained:
Simplifying Eq. 8:
in which K = a constant varying with air temperature and atmospheric pressure,
in units of
In Eq. 10, the units of ρa, cp, ρ, λ, and γ are the same as in Eqs. 2 and 4. The psychrometric constant γ, in mb/°C, is:
in which cp = specific heat of moist air,
in cal/(gr-°C); p = atmospheric pressure, in mb;
Substituting Eq. 11 in Eq. 10:
in which the constant K remains in units of s/(d-mb). Replacing rMW = 0.622 into Eq. 12:
in which the constant K remains in units of s/(d-mb).
At T = 20°C and standard atmospheric pressure (sea level):
ρa = 0.0012046
in which:
6. EXTERNAL RESISTANCE The external, or aerodynamic resistance ra varies with the surface roughness (water, soil, or vegetation), being inversely proportional to wind speed (Eq, 15). In other words, the external conductance and, thus, the evaporation rate, increases with wind speed, as originally postulated by Dalton (Ponce, 1989). The external resistance for evaporation from open water can be estimated as follows:
in which:
The external resistance ra (s/m) for the reference crop (clipped grass 0.12-m high), for measurements of wind speed (m/s), temperature and humidity at a standardized height of 2 m is:
For instance, for v2 = 200 km/d = (200000 m) / (86400 s) = 2.31 m/s, the external or aerodynamic resistance of the reference crop is:
7. INTERNAL RESISTANCE The internal, or stomatal or surface resistance rs is inversely proportional to the leaf-area index L. An empirical relation for surface resistance is (Maidment, 1993):
in which rs is in s/m. The leaf-area index L is empirically related to crop height hc. The leaf-area index for clipped grass is:
in which hc = crop height, in m,
varying in the range From Eqs. 18 and 19, the surface resistance of the reference crop (clipped grass 0.12-m high) is: rsrc = 200 / (24 × 0.12) = 69.4 s/m. The leaf-area index for alfalfa is:
in which
crop height hc is in m, varying in the range
From Eq. 20, for hc = 0.3 m, the leaf-area index for alfalfa is: L = 3.69. From Eq. 18, the surface resistance for alfalfa is: rs = 200 / 3.69 = 54.2 s/m.
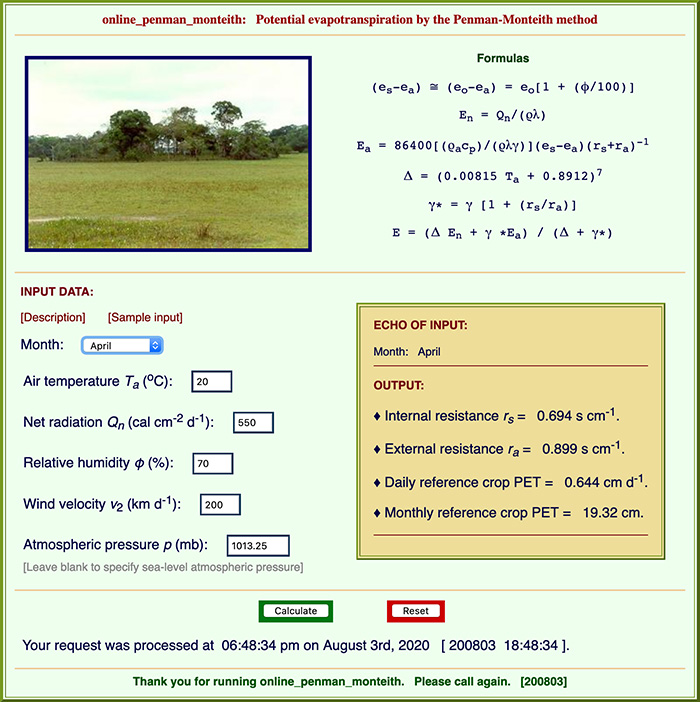
8. ILLUSTRATIVE EXAMPLE
Calculate the evaporation rate of the reference crop (clipped grass) by the Penman-Monteith method for the month of April,
for the following atmospheric conditions: air temperature Ta =
20°C; net radiation Qn = 550 cal/(cm2-d);
wind speed v2 = 200 km/d; and relative humidity φ = 70%.
Assume standard atmospheric pressure.
Solution.
Δ = (0.00815 Ta + 0.8912)7 = 1.447 mb/°C.
En = Qn / ( ρ λ ) = 550 / (0.99821 × 586) = 0.94 cm/d
rarc = (208 × 86400) / (200 × 1000) = 90 s/m = 0.9 s/cm
rsrc = 200 / (24 x 0.12) = 69.4 s/m = 0.694 s/cm
γ = (0.2402 × 1013.25 ) / (586 × 0.622) = 0.668
γ * = 0.668 [ 1 + (0.694 / 0.9 ) ] = 1.18
(es - ea) ≅ (eo - ea)
= eo [ 1 - (φ / 100) ] = 23.37 [ 1 - (70 / 100)] = 7.01 mb.
Ea = ( 0.064 × 7.01 ) / ( 0.9 + 0.694 ) = 0.2815 cm/d.
E = [ ( 1.447 × 0.94 ) + ( 1.18 × 0.2815 ) ] / ( 1.447 + 1.18 ) = 0.644 cm/d.
ONLINE CALCULATION.
Using ONLINE PENMAN MONTEITH, the answer
is: Daily reference crop
REFERENCES
Maidment, D. R. 1993. Handbook of Hydrology. McGraw-Hill.
Ponce, V. M. 1989. Engineering Hydrology: Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey.
Ponce, V. M. 2014.
Engineering Hydrology: Principles and Practices. Online text.
|
| 200808 09:30 |