1. INTRODUCTION Irrigation canal gates should be opened or closed at sufficiently slow speeds: otherwise, surface transients may develop that could negatively impair the operation of the canal. We use an analytical model of unsteady open-channel flow to develop a criterion for the time of opening of an irrigation canal gate. The criterion is based on the fact that in typical canal situations, the longer the wavelength of the disturbance, the faster its attenuation rate is. A practical criterion is developed by first converting wavelength into wave period and then linking the wave period with the time of opening. 2. CRITERION FOR TIME OPENING Ponce and Simons' (1977) analytical model of unsteady open-channel flow can be used to calculate attenuation rates of small-amplitude surface transients across the entire spectrum of shallow water waves, from kinematic to gravity waves. Specifically, we focus on the dimensionless wave numbers close to the border between dynamic and gravity waves, herein referred to as border dimensionless wave numbers. To increase the usefulness of the analysis, we express the dimensionless wave number σ* as dimensionless wave period τ* (Ponce et al. 1978). Border dimensionless wave numbers and corresponding dimensionless wave periods are strongly dependent on the steady-flow Froude number (Ponce and Simons 1977). To reduce this dependence, we normalize the dimensionless wave period by dividing it by the square of the Froude number, a technique that emulates Woolhiser and Liggett's (1967) kinematic flow number. The normalized dimensionless wave period is:
For a given Froude number, we determine the normalized dimensionless wave period that will produce a
The dimensionless wave period is τ * = (TuoSo) / do, in which T = wave period; uo = steady-flow mean velocity; do = steady-flow depth: and So = channel slope (Ponce et al. 1978); and the steady-flow Froude number is Fo = uo / (gdo)1/2, which g = gravitational acceleration (Chow 1959). Thus, the normalized dimensionless wave period reduces to:
Table 1 shows calculated values of τ'** for selected Froude numbers in the range of 0.1-0.5. Froude numbers substantially less than 0.1 were deemed impractical because of the possibility of excessive sedimentation. Froude numbers greater than 0.5 were not considered further because of decreased attenuation rates and associated potential for surface instabilities. Table 1 shows that τ'** varies slightly with Froude number; however, the range of variation is shown to be much smaller than that of the border dimensionless wave numbers (Ponce and Simons 1977).
3. TIME OF OPENING OF CANAL GATE The developed criterion can be summarized as follows: For a given steady-flow Froude number, the normalized dimensionless wave period (Eq. 2) should be greater than or equal to the respective threshold value τ'**
The wave period T is associated with the period of the main surface disturbance. As a first approximation, we assumed the time of opening To to be equal to half of the wave period. Therefore:
In terms of the Manning friction and SI units, Eq. 4 can be expressed as follows:
in which n = Manning coefficient (Chow 1959). In terms of Manning friction and U.S customary units, Eq. 4 can be expressed as follows:
4. APPLICATION TO IMPERIAL VALLEY CANAL DATA
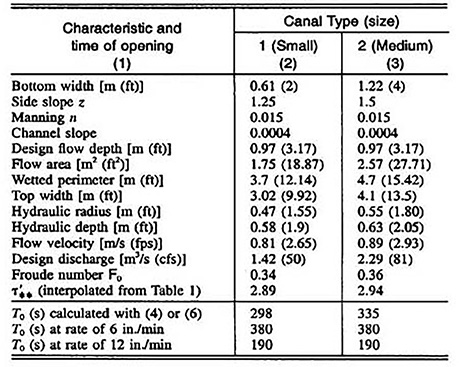
The developed criterion (Eqs. 4-6) is applied to two typical irrigation canal designs in the Imperial Valley, California. The hydraulic data were supplied by the Imperial Irrigation District's Engineering Division in Brawley, Imperial County. Canal 1 is small, with a 2-ft bottom width; Canal 2 is medium-sized, with a 4-ft bottom width. The hydraulic characteristics are shown in Table 2, together with the time of opening calculated using Eq. 5 or 6. Also shown is the actual time of opening, based on two rates-of-rise recommended by the manufacturers,
| |||||||||||||||||||||||||||||||||||||||||||||||
| 211230 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |