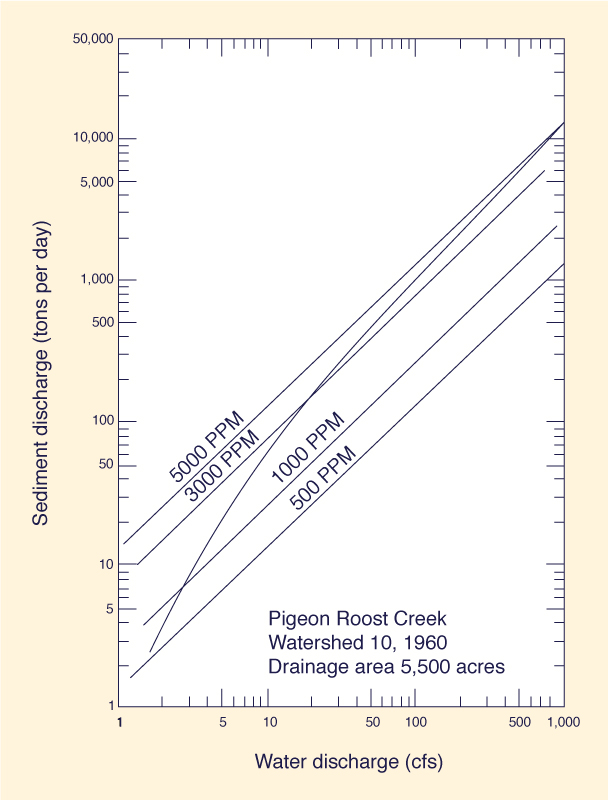
1.  INTRODUCTION

In engineering practice, the sediment rating curve is used to relate sediment discharge to water discharge, under steady equilibrium flow conditions. The slope of the sediment rating curve is a measure of the suspended bed material sediment concentration. In this paper, the suspended bed material sediment concentration is referred to as sediment concentration, and it specifically excludes wash load.

Typically, sediment rating curves plotted in logarithmic scale have large slopes at low discharges and smaller slopes at high discharges, as shown in Fig. 1 (1). For a sufficiently high discharge, the slope of the sediment rating curve approaches asymptotically a value of unity, i.e., a constant sediment concentration. This constant sediment concentration which streams tend to reach at high discharges is herein referred to as the ultimate sediment conoentration. As shown in this paper, the ultimate sediment concentration can be readily calculated as a function of flow and bed material sediment properties.

2.  ULTIMATE SEDIMENT CONCENTRATION

In engineering practice, the following power function is commonly used to provide a fit between measured water and sediment discharge data:

Qs  =  c Q m

(1)

in which Q_s = suspended bed material sediment discharge, hereafter sediment discharge for simplicity, Q = water discharge, and c and m, coefficient and exponent of the rating, respectively.

In Eq. 1, for m = 1, the sediment concentration is independent of Q and equal to:

Cs'  =  c

(2)

in which C_s' = ultimate sediment concentration. The value of m = 1 appears to be a minimum value approached by many streams at very high flood discharges (Ref. 1, p. 476).

A widely used sediment transport formula which is based on Colby's method (2) is the following:

qs  =  k ρ v n

(3)

in which q_s = sediment discharge, per unit channel width; v = mean flow velocity; k = (suspended bed material) sediment transport parameter, a function of bed material sediment properties, including mean particle size, gradation, and specific gravity; ρ = density of water; and n = exponent. The value of n is usually in the range 3-7.

Colby (2) has shown that high values of n prevail at low water discharges, while low values of n are typical of high water discharges. Since n cannot realistically decrease below 3, the value n = 3 is taken as the exponent associated with the ultimate sediment concentration. In this case, the bed configuration approaches upper regime (e.g., plane bed with sediment movement), in which bottom friction is largely due to grain roughness (5).

With n = 3, Eq. 3 is dimensionally homogeneous:

qs  =  k ρ v 3

(4)

in which q_s = ultimate sediment discharge, per unit channel width, and k is a dimensionless parameter.

The water discharge, per unit channel width, is:

q  = v d

(5)

in which d = flow depth.

In terms of discharge per unit channel width, Eq. 2 is recast as:

qs Cs  =  ______               q

(6)

Substitution of Eqs. 4 and 5 into Eq. 6 leads to:

Cs  = k F 2 γ

(7)

in which

γ  = ρ g

(8)

is the specific weight of water, g = gravitational acceleration, and

v F  =  ___________            (gd )1/2

(9)

is the steady equilibrium flow Froude number.

Equation 7 can be used in either calibration or prediction mode. In calibration mode, the Froude number and ultimate sediment concentration are known, and Eq. 7 is used to solve for the sediment transport parameter k. In prediction mode, the Froude number and parameter k are known, and Eq. 7 is used to solve for C_s'. For example, with k = 0.1, and F = 0.2, Eq. 7 leads to:

C_s' = 0.1 × 0.04 x 1,000 g/L = 4 g/L = 4,000 ppm.

An alternate expression to Eq. 7 can be derived by noting that for wide channels, the following expression relates friction (or bottom) slope to Froude number, under steady equilibrium (i.e. uniform flow in the case of artificial channels) flow conditions (3):

So  = f  F 2

(10)

in which S_o = bottom slope, and

g f  =  ______           C 2

(11)

in which f = dimensionless Chezy friction factor, and C = Chezy coefficient. Combining Eqs. 7 and 10:

k So Cs'  =  ________ γ                 f

(12)

Given Eq. 12, the ultimate sediment concentration can be calculated as a function of the following three dimensionless parameters: (1) sediment transport parameter k, (2) bottom slope S_o , and (3) friction factor f. For example, with C = 70 m^1/2/s, S_o = 0.0084, and k = 0.05, the application of Eqs. 11 and 12 leads to: C_s' = 10,000 ppm.

In practice, the parameter k is a measure of the flow's ability to entrain and transport bed material sediment. It accounts not only for mean particle size, gradation, and specific gravity, but also for the effect of wash load concentration and water temperature on bed material transport (2).

3.  SUMMARY AND CONCLUSIONS

Typical sediment rating curves show a trend toward a constant (suspended bed material) sediment concentration at sufficiently high discharges. This maximum value of sediment conoentration can properly be referred to as the ultimate sediment concentration.

The ultimate sediment ooncentration is shown to be a function of a dimensionless (bed material) sediment transport parameter and a dimensionless flow parameter (the square of the Froude number). Alternatively, the Froude number squared can be expressed as the ratio of bottom slope and dimensionless Chezy friction factor.

Fig. 1   Typical sediment rating curve (1). 4.  APPLICATIONS Equation 7 may be used for the calculation of suspended bed material sediment concentration at high flood discharges. For instance, a sediment transport formula applicable to high discharges is needed in the calculation of gradual earth dam breaches, whether postulated or hindcasted. The sediment transport parameter k may be used as a calibration parameter, to be determined based on ultimate sediment concentration data, or alternatively, in a prediction mode once its value has been established. Limited experience to date suggests that k is normally restricted within a relatively narrow range (4). Sediment rating curves under a wide range of water discharges are relatively scarce (Ref. 1, p. 476). Therefore, extrapolations are commonly made to encompass the range of high flood discharges. Extrapolations which do not take into account the ultimate sediment concentration are bound to result in unrealistically high values of sediment discharge. In extreme cases, the sediment discharge extrapolated in such a way may result in a concentration exceeding 1,000,000 ppm, which is clearly physically impossible. Therefore, additional research is needed to clarify the physical mechanisms governing the attainment of the ultimate sediment concentration. APPENDIX 1. REFERENCES ASCE. 1975. "Sedimentation Engineering," Manual No. 54. Colby, B. R. 1964. "Discharge of sands and mean velocity relations in sand-bed streams," Profeasional Paper No. 462-A, U.S. Geological Survey, Washington, D.C. Lighthill, M. J., and G. B. Whitham. 1955. "On kinematic waves. I. Flood movement in long rivers," Proceedings of the Royal Society of London, Vol. A229, May, pp. 281-216. Ponce, V. M., and A. J. Tsivoglou. 1981. "Modeling gradual dam breaches," Journal of the Hydraulics Division, ASCE, Vol. 107, No. HY7, July, pp. 829-838. Simons, D. B. and E. V. Richardson. 1966. "Resistance to flow in alluvial channels," Professional Paper 422-J, Washington, U.S. Geological Survey, Washington, D.C. APPENDIX 2. NOTATION The following symbols are used in this paper: C = Chezy coefficient; Cs' = ultimate (suspended bed material) sediment concentration; c = coefficient of sediment rating curve; d = flow depth; F = steady equilibrium flow Froude number; f' = dimenaionless Chezy friction factor; g = gravitational acceleration; k = (suspended bed material) sediment transport parameter; m = exponent of sediment rating curve; n = exponent of sediment discharge formula; Q = water discharge; Qs = (suspended bed material) sediment discharge; q = water discharge, per unit channel width; qs = (suspended bed material) sediment discharge, per unit channel width; qs' = ultimate (suspended bed material) sediment discharge, per unit channel width; S0 = friction or bottom slope; v = mean flow velocity; γ = specific weight of water; and ρ = density of water.