1.  INTRODUCCIÓN

En este artículo se desarrolla un modelo numérico de agua subterránea, el cual es estable y convergente. Siendo la estabilidad una condición necesaria para la operación del modelo, el énfasis está en la convergencia, es decir, si el modelo numérico puede reproducir la ecuación diferencial con suficiente precisión.

Una característica importante del modelo es su simplicidad, lo cual lo hace atractivo y útil para una amplia variedad de aplicaciones. El modelo numérico es una formulación explícita de la ecuación bidimensional de difusión (x-y) del flujo en medios porosos para un acuífero isotrópico homogéneo. Las fuentes (percolación por lluvia y/o riego) y los sumideros (bombeo) se tienen en cuenta en la formulación. Las condiciones de contorno se especifican como: (a) altura o flujo, y (b) permeable o impermeable.

Un enfoque específico del desarrollo del modelo es la evaluación de la estabilidad y convergencia. Los modelos explícitos están sujetos a un estricto criterio de estabilidad, que debe cumplirse si el modelo va a simular las condiciones naturales en forma realística (O'Brien et al. 1949; Douglas 1956). Como se muestra aquí, el modelo también debe satisfacer un criterio de convergencia para poder mantener la precisión. La satisfacción tanto de la estabilidad como de la convergencia requiere que el número de Reynolds de la célula D sea igual a 1.

Después de más de 20 años de desarrollo de modelos implícitos de flujo de agua subterránea, la elección de un modelo explícito en este momento requiere una explicación más convincente. Es bien sabido que los modelos implícitos son incondicionalmente estables. Menos conocido es el hecho de que los modelos implícitos están sujetos a un criterio de convergencia que efectivamente establece un límite superior en el intervalo de tiempo. Ponce et al. (1978; 1979) han documentado ejemplos de falta de convergencia en los modelos de aguas superficiales y transporte de sedimentos. Por lo tanto, cuando se tiene en cuenta su complejidad adicional, los modelos implícitos pueden no ser necesariamente mejores que los modelos explícitos.

2.  FORMULACIÓN DEL MODELO

La ecuación tridimensional de difusión del flujo a través de medios porosos es (Rushton y Redshaw 1979; Kresic 1997):

∂               ∂h             ∂             ∂h             ∂              ∂h                           ∂h ____ ( Kx  _____ )  +  ____ ( Ky _____)  +  ____ ( Kz _____ )  +  W  =  Ss  ____  ∂x              ∂x            ∂y            ∂y             ∂z             ∂z                           ∂t

(1)

en la cual h = carga piezométrica [L]; K_x, K_y, y K_z son las conductividades hidráulicas a lo largo de los ejes de coordenadas x, y, y z, respectivamente [LT^-1]; W = flujo volumétrico por unidad de volumen, representando ya sea fuentes (+) o sumideros (-) [T^-1]; S_s = almacenamiento específico del material poroso [L^-1]; y t = tiempo.

En dos dimensiones en el plano, la Ec. 1 se simplifica a:

∂               ∂h             ∂             ∂h                           ∂h ____ ( Kx  _____ )  +  ____ ( Ky _____)  +  W  =  Ss  ____  ∂x              ∂x            ∂y            ∂y                            ∂t

(2)

Suponiendo un acuífero homogéneo isotrópico de conductividad hidráulica K:

∂2h        ∂2h                           ∂h  K (  _____  +  _____ ) +  W  =  Ss  ____           ∂x2         ∂y2                          ∂t

(3)

Definiendo la difusividad hidráulica del acuífero (Freeze y Cherry 1979) como sigue:

K  ν =  _____            Ss

(4)

conduce a:

∂2h        ∂2h          νW          ∂h  ν ( _____  +  _____ ) +  _____  =  ____          ∂x2        ∂y2            K           ∂t

(5)

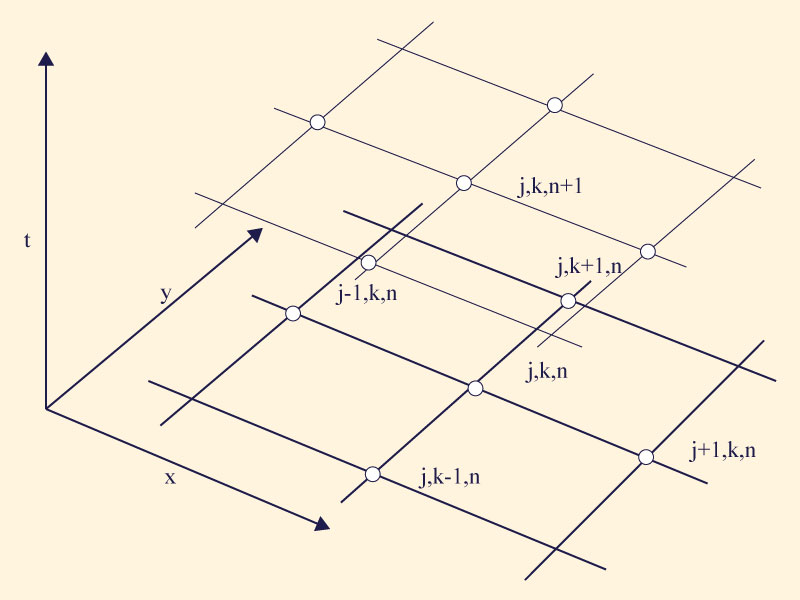
La Ecuación 5 representa el flujo bidimensional en un acuífero homogéneo isotrópico de propiedades K y ν y el término fuente/sumidero W. Un esquema simple y apropiado en diferencias finitas de primer orden en el tiempo y segundo orden en el espacio es (Fig. 1):

n + 1      n                n           n        n                 n           n        n     hj,k    - hj,k             hj+1,k - 2hj,k  + hj-1,k           hj,k+1  - 2hj,k + hj,k-1         ν ___________ =   ν  ___________________ +  ν __________________ + ( ____ ) Wj,k        Δt                              (Δx)2                                (Δy)2                 K

(6)

Fig. 1   Notación para el esquema de diferencias finitas.

El intervalo espacial se establece como Δs = Δx = Δy. Siguiendo a Roache (1972), definimos un tipo de número de Reynolds de célula como la relación entre las difusividades física y numérica. Esto lleva a:

ν                   Δt D  =  ________  =  4ν  ______           (Δs /2)2            (Δs)2           _______               Δt

(7)

La Ec. 6 se reduce a:

n+1           n                        n              νΔt h j, k  =  D h̄ j, k +  ( 1 - D ) h j, k   +  ( _____ ) Wj, k                                                              K

(8)

en la cual:

n               n               n               n                 h j +1, k  +  h j -1, k  +  h j, k+1  +  h j, k -1                                                     n h̄ j, k =     _____________________________________________                                             4

(9)

El término fuente promediado en el tiempo, en unidades de velocidad, es el siguiente:

r j, k W j, k =   ______                   b

(10)

en la cual r_j,k = tasa de percolación [LT^-1] (debido a lluvia y/o riego) en el nodo espacial (j, k), y b = profundidad del acuífero [L].

El término sumidero promediado en el tiempo, en unidades de caudal, es el siguiente:

p j, k W j, k =  -  ________                  b (Δs)2

(11)

en la cual p_j,k = tasa de bombeo [L³ T^-1] en el nodo espacial (j ,k).

Como la transmisividad es:

T = Kb

(12)

y la difusividad es:

T ν =  _____          S

(13)

en cual S = coeficiente de almacenamiento (Freeze y Cherry 1979), la Ec. 8 se reduce a lo siguiente:

n+1            n                       n               Δt                          Δt h j, k  =  D h̄ j, k +  ( 1 - D ) h j, k   +  ( _____ ) r j, k  -  [ _________ ] p j, k                                                              S                      S (Δs)2

(14)

Con las Ecuaciones 7 y 13, la Ec. 14 se reduce a lo siguiente:

n+1            n                         n             D (Δs)2                    D h j, k  =  D h̄ j, k  +  ( 1 - D ) h j, k   +  [ ________ ] r j, k  -  ( _____ ) p j, k                                                                4T                        4T

(15)

Para el caso especial D = 1, la eq. 15 se reduce a:

n+1         n            (Δs)2                    1 h j, k  =  h̄ j, k  +  [ ______ ] r j, k  -  ( _____ ) p j, k                               4T                      4T

(16)

La Ecuación 15 calcula la altura piezométrica en el nodo desconocido (j, k, n+1) en función de la altura piezométrica promedio h̄_j,kⁿ en los cuatro nodos conocidos adyacentes a (j, k, n), la tasa de percolación r_j,k, la tasa de bombeo p_j,k, el intervalo espacial Δs, y la transmisividad T (Fig. 1).

3.  CONDICIONES DE CONTORNO

Las condiciones de contorno pueden ser del tipo Dirichlet o Neumann (Kinzelbach 1986). Las condiciones de Dirichlet especifican la altura h;las condiciones de Neumann especifican el flujo, es decir, el gradiente de altura ∂h/∂x ortogonal al límite. En general, las condiciones de Dirichlet conducen a una frontera permeable, ya que el flujo suele ser finito. Las condiciones de Neumann son tipo A (permeables) o tipo B (impermeables). Una condición de Neumann tipo A especifica un gradiente finito, es decir, ∂h/∂x ≠ 0; por otro lado, una condición de Neumann tipo B especifica un gradiente cero, es decir, ∂h/∂x = 0.

Las condiciones de Neumann tipo A pueden especificarse mediante extrapolación lineal de los dos nodos interiores inmediatamente vecinos. La extrapolación lineal da como resultado un gradiente finito, que equivale a una frontera permeable. Las condiciones de Neumann tipo B pueden especificarse mediante la reubicación del nodo interior vecino; la reubicación da como resultado un gradiente cero, lo que equivale a una frontera impermeable.

Las condiciones de Neumann mixtas tipo A/tipo B, apropiadas para fronteras semipermeables o flujos de entrada que varían temporalmente, se pueden especificar de la siguiente manera:

n+1                       n+1               n+1 h j, k  =  ( 1 + α ) h j - 1 ,k  -  αh j - 2 ,k

(17)

en el cual j = nodo límite, y α = factor de ponderación, variando en el rango 0 ≤ α ≤ 1, tal que α = 0 representa un límite impermeable, y α = 1 un límite permeable.

4.  MODELO DE PRUEBA

El modelo se sometió a las siguientes cuatro pruebas para examinar sus propiedades numéricas:

1. Prueba de arranque en caliente, permebale

Esta condición prueba la capacidad del modelo para volver a la condición de referencia de equilibrio estable, siguiendo la especificación de: (a) una capa freática abatida como condición inicial, ( b) fronteras permeables, y (c) ausencia de bombeo.

2. Prueba de arranque en frío, permeable

Esta condición prueba la capacidad del modelo para lograr un cono de depresión de equilibrio estacionario siguiendo la especificación de: (a) la condición inicial de equilibrio estacionario de referencia, ( b) fronteras permeables, y (c) bombeo.

3. Prueba de arranque en caliente, impermeable

Esta condición prueba la capacidad del modelo para volver a una condición de equilibrio estacionario, fuera de la línea de base, siguiendo la especificación de: (a) una capa freática abatida como condición inicial, ( b) fronteras impermeables, y (c) ausencia bombeo.

4. Prueba de arranque en frío, impermeable

Esta condición prueba la capacidad del modelo para simular el agotamiento lineal del acuífero siguiendo la especificación de: (a) la condición inicial de equilibrio estacionario de referencia, (b) frontera impermeables, y (c) bombeo.

Pruebas de convergencia

Primero, se probó la convergencia del modelo de agua subterránea (O'Brien et al. 1949). Para este propósito, se utilizó una prueba permeable de arranque en caliente, en la que la recuperación completa de la altura a la condición de línea base de equilibrio estable es una prueba de la convergencia del modelo.

La especificación del prototipo de prueba era un acuífero de planta cuadrada, de 100 km² (10 km x 10 km), de transmisividad T = 0.01 m² s^-1, y coeficiente de almacenamiento S = 0.1. Dada la Ec. 13, la difusividad hidráulica es ν = 0.1 m² s^-1. El intervalo espacial se fijó en Δs = 100 m, es decir, un total de 101 × 101 = 10201 nodos de la malla, etiquetados (0,0) a (100,100).

La estabilidad requiere que D ≤ 1. Por lo tanto, D = 1 es el número máximo de Reynolds de la célula que se puede utilizar en la práctica. Para D = 1, el intervalo de tiempo se fija en el siguiente valor (Ec. 7):

(Δs)2 Δt  =  ______              4ν

(18)

Se realizó una serie de dieciséis (16) corridas para probar la convergencia del modelo de agua subterránea bajo el número de Reynolds de la célula variable D y la altura de referencia h_ref (condición de referencia de equilibrio estacionario). La condición inicial se especificó como h₀ = (h_ref - 100) en un área cuadrada de 5 km × 5 km ubicados en el medio del campo computacional (51 × 51 = 2601 nodos de cuadrícula).

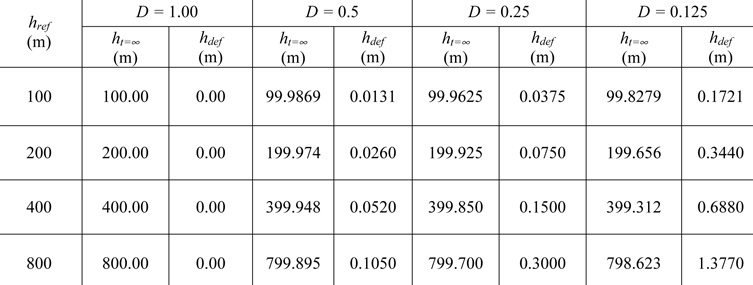
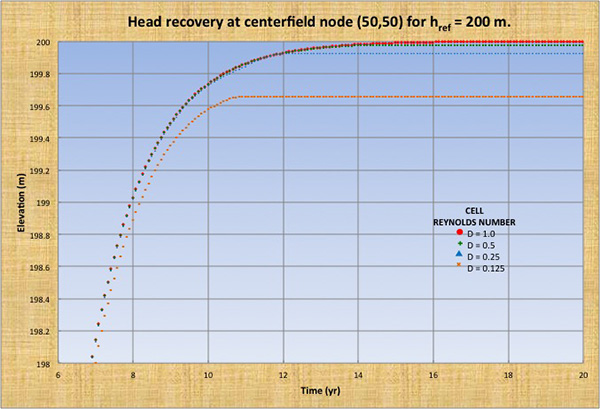
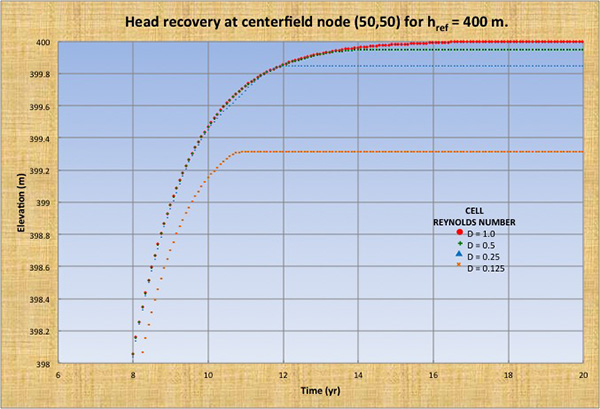
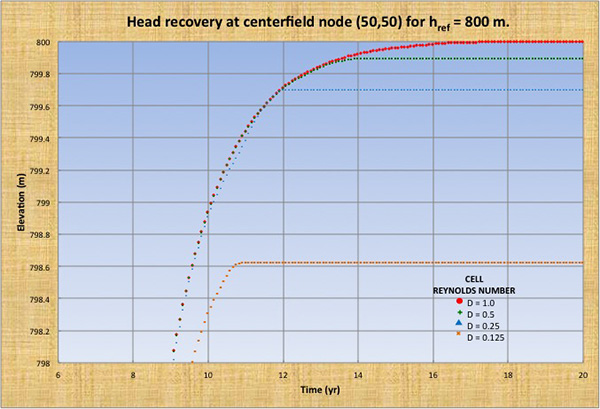
Se eligieron cuatro números de Reynolds de al célula (D = 1.0, 0.5, 0.25 y 0.125) y cuatro alturas de referencia (h_ref = 100, 200, 400 y 800 m). El fondo del acuífero se fijó en h_fondo = 0 m. De la Ec. 18, el intervalo de tiempo para D = 1.0 es Δt = 6.944 h. Por tanto, los intervalos de tiempo a utilizar en la serie de ensayos son: Δt = 6.944, 3.472, 1.736 y 0.868 h, correspondientes a D = 1.0, 0.5, 0.25 y 0.125, respectivamente.

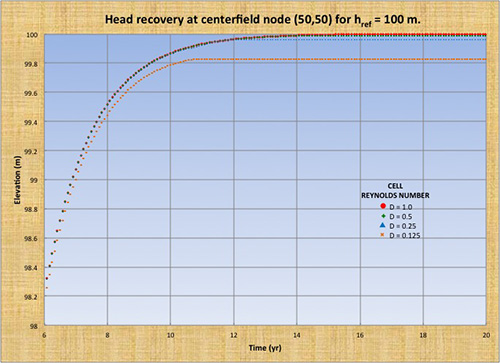
Las Figuras 2 (a) a (d) muestran la recuperación de la altura en el nodo del campo central (50, 50) para alturas de referencia h_ref = 100, 200, 400 y 800 m, y celda números de Reynolds de la célula D = 1.0, 0.5, 0.25 y 0.125. Para valores distintos a D = 1, existe un déficit de recuperación de altura, lo que indica la incapacidad del modelo para volver a la condición de referencia de equilibrio estable, es decir, falta de convergencia. La Tabla 1 muestra el déficit de recuperación de altura h_def en función de la altura de referencia h_ref y el número de Reynolds de la célula D.

Tabla 1. Déficit de recuperación de altura hdef en función de la altura de referencia href y el número de Reynolds de la celda D.

Fig. 2 (a)  Recuperación de la altura en el nodo del campo central (50,50) para href = 100 m.

Fig. 2 (b)  Recuperación de la altura en el nodo del campo central (50, 50) para href = 200 m.

Fig. 2 (c)  Recuperación de la altura en el nodo del campo central (50, 50) para href = 400 m.

Fig. 2 (d)  Recuperación de la altura en el nodo del campo central (50, 50) para href = 800 m.

Las siguientes conclusiones se extraen de la Fig. 2 y la Tabla 1:

1. El déficit de recuperación de altura h_def = 0, es decir, la recuperación de altura es completa, solo para D = 1.

2. El déficit de recuperación de altura aumenta de forma no lineal con disminuciones en el número de Reynolds de la célula de 1.0 a 0.125.

3. El déficit de recuperación de altura aumenta linealmente con aumentos en la altura de referencia, de 100 a 800 m.

4. La condición D = 1 no sólo es la más precisa sino también la más económica. Para valores más pequeños de D, el modelo es menos convergente y la ejecución requiere más timepo de procesador y tiempo total para ser completada.

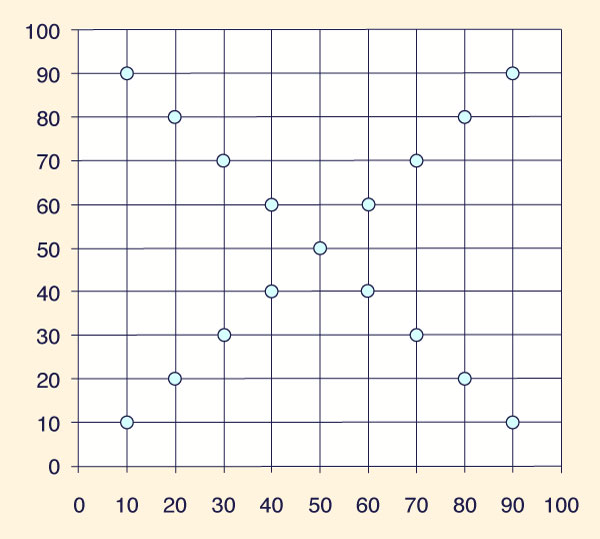
Pruebas permeables/impermeables caliente/frío

Las pruebas de permeabilidad/impermeabilidad caliente/frío se llevaron a cabo especificando la misma geometría y propiedades del acuífero que para las pruebas de convergencia. El número de Reynolds de la celda se fijó en D = 1, lo que conduce a Δt = 6.944 h.

Para las pruebas en caliente, la altura de referencia se establece en h_ref = 500 m y la condición inicial se especifica como h₀ = (h_ref - 100) en un área cuadrada de 5 km × 5 km ubicado en el medio del campo computacional. El fondo del acuífero se establece en h_fondo = 0 m. Por tanto, el volumen del acuífero en equilibrio estacionario es de 50,000 hm³.

Para las pruebas en frío, la altura de referencia h_ref = 500 m se especifica como condición inicial en cada nodo y el fondo del acuífero se establece en h_fondo = 0 m. Por lo tanto, el volumen del acuífero en equilibrio estacionario es de 50,000 hm³. Una batería de diecisiete (17) bombas se coloca simétricamente en el campo, a una distancia de 1414.2 m entre sí, formando una X (Fig. 3), y cada una bombeando p = 250 Ls^-1.

Fig. 3  Ubicaciones de la bomba para pruebas de arranque en frío.

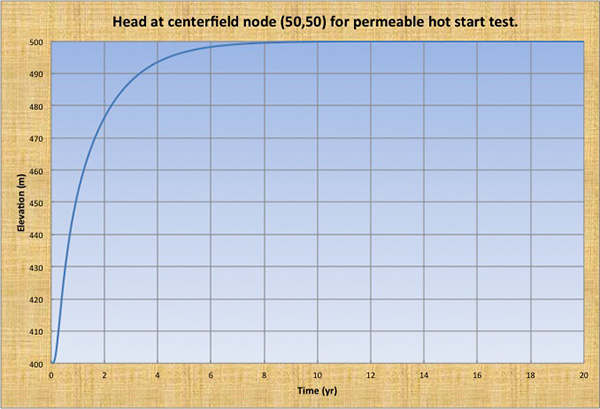
Prueba permeable en caliente

El volumen inicial del acuífero es de 47,399 hm³. El nivel piezométrico volvió a la condición de equilibrio estable (h = 500 m en cada nodo) de forma asintótica después de 15.85 años de simulación (Fig. 4). La simulación fue fuertemente estable y convergente. El volumen del acuífero calculado, una vez alcanzada la condición de equilibrio estacionario, fue de 50,000 hm³.

Fig. 4  Altura en el nodo del campo central (50,50) para la prueba permeable en caliente.

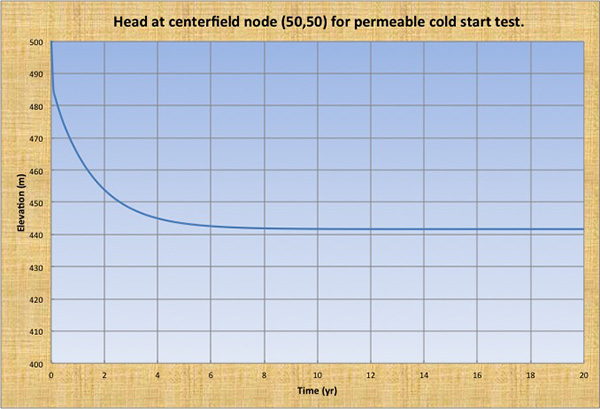
Prueba permeable en frío

El volumen inicial del acuífero es de 50,000 hm³. El nivel piezométrico alcanzó una condición de equilibrio estable, con el agotamiento máximo (h = 441.662 m) en el nodo del campo central (50,50), de manera asintótica después de 12.43 años de simulación (Fig. 5). La simulación fue fuertemente estable. El volumen acuífero calculado fue de 48,218 hm³. La conservación del volumen, calculada tomando el volumen inicial del acuífero, restando el volumen bombeado y sumando las afluencias de los límites, fue del 99.98% al final de 20 años de simulación.

Fig. 5  Altura en el nodo del campo central (50, 50) para la prueba permeable en frío.

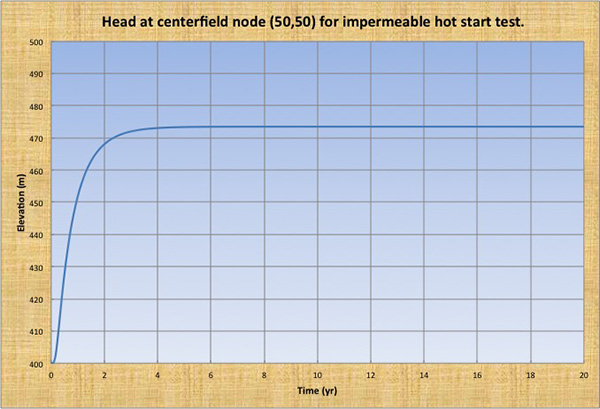
Prueba impermeable en caliente

El volumen inicial del acuífero es de 47,399 hm³. El nivel piezométrico alcanzó una condición de equilibrio estable (h = 473.462 m en cada nodo) de manera asintótica después de 8.34 años de simulación (Fig. 6). La simulación fue fuertemente estable. El volumen del acuífero calculado, una vez alcanzada la condición de equilibrio estacionario, fue de 47,349 hm³. La conservación del volumen, calculada como la relación entre el volumen calculado y el volumen inicial del acuífero, fue del 99.89 % al final de 20 años de simulación.

Fig. 6  Altura en el nodo del campo central (50, 50) para prueba impermeable en caliente.

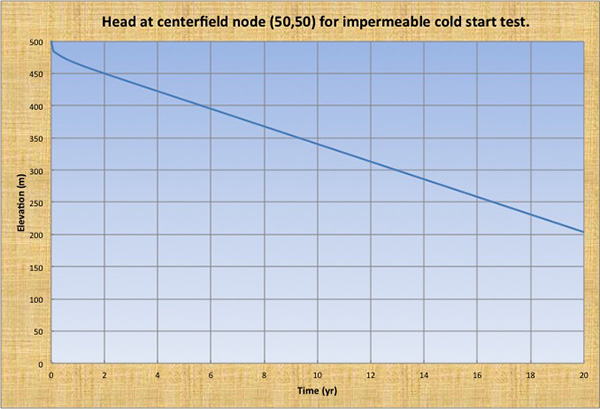
Prueba impermeable en frío

El volumen inicial del acuífero es de 50,000 hm³. El nivel piezométrico disminuyó de forma lineal, con el agotamiento máximo (h = 203.905 m) en el nodo del campo central (50,50) después de 20 años de simulación (Fig. 7). La simulación fue fuertemente estable. El volumen del acuífero calculado al final de 20 años de simulación fue de 22,687 hm³, es decir, el 45.37% del volumen inicial del acuífero.

Fig. 7  Altura en el nodo del campo central (50,50) para prueba impermeable en frío.

5.  RESUMEN Y CONCLUSIONES

Se ha desarrollado y probado un modelo de agua subterránea bidimensional estable y convergente de un acuífero isotrópico homogéneo bajo una amplia gama de condiciones de flujo. El modelo es explícito y puede dar cuenta de lo siguiente: (a) fuentes/sumideros, y (b) condiciones de frontera de altura/flujo y permeables/impermeables. Una característica importante del modelo es que establece el número de Reynolds de la celda D = 1 para satisfacer tanto la estabilidad como la convergencia.

Las pruebas del modelo en condiciones hipotéticas mostraron que el modelo es estable, convergente, y que conserva masa. La prueba permeable en caliente convergió a la condición de referencia de equilibrio estable después de 15.85 años. La prueba permeable en frío convergió a un cono de depresión de equilibrio estable después de 12.43 años. La prueba impermeable en caliente convergió a una condición de equilibrio estable después de 8.34 años. La prueba impermeable en frío simuló correctamente el agotamiento lineal del acuífero.

Bibliografía

Douglas, Jr., G. 1956. On the relation between stability and convergence in the numerical solution of linear parabolic and hyperbolic equations. Journal of Society of Industrial and Applied Mathematics, 4, 20-37.

Freeze, y Cherry. 1979. Groundwater. Prentice Hall, Englewood Cliffs, New Jersey.

Kilzenbach, W. 1986. Groundwater modelling: An introduction with sample programs in BASIC. Developments in Water Science No. 25, Elsevier, Amsterdam, The Netherlands.

Kresic, N. 1979. Quantitative solutions in hydrogeology and groundwater modeling. Lewis Publishers, New York.

O'Brien, G. G. Hyman, y M. A. Kaplan. 1950. A study of the numerical solution of partial differential equations. Journal of Mathematics and Physics, 29(4), 231-251.

Ponce, V. M., H. Indlekofer, y D. B. Simons. 1978. Convergence of four-point implicit water wave models. Journal of the Hydraulics Division , ASCE, 104(HY7), 947-958.

Ponce, V. M., H. Indlekofer, y D. B. Simons. 1979. The convergence of implicit bed transient models. Journal of the Hydraulics Division, ASCE, 105(HY4), 351-363.

Roache, P. 1972. Computational fluid dynamics. Hermosa Publishers, Albuquerque, NM.

Rushton, K. R., y S. C. Redshaw. 1979. Seepage and groundwater flow; numerical analysis by analog and digital methods. John Wiley and Sons, New York.