1.  INTRODUCTION

The Muskingum-Cunge method of flood routing is well established in the hydrologic engineering literature (Cunge, 1969; Ponce and Yevjevich, 1978; U.S. Army Corps of Engineers, 1990). It is a convenient method because the routing parameters are a function of channel properties and grid specification, which leads to results which are independent of grid size. The method has linear and nonlinear modes. In the linear mode, average flow values are used to calculate the routing parameters at the start of the computation, and these are kept constant throughout the computation in time. In the nonlinear mode, the routing parameters are recalculated for every computational cell as a function of local flow values.

Both modes of computation have their advantages and disadvantages. The linear mode conserves mass, but it requires a priori estimation of a reference flow on which to base the computation of the routing parameters. In addition, the routed flows lack the steepening exhibited by inbank flood waves. Conversely, the nonlinear mode does not require the specification of a reference flow and can simulate the wave steepening. Unfortunately, the nonlinear mode is saddled with a small but perceptible loss of mass.

Given the trade-offs involved, it seems certain that both routing modes will continue to be used in the future. The linear mode will be used where simplicity is desired, notwithstanding its lack of wave steepening. The nonlinear mode will be used where the simulation of wave steepening is judged to be important, albeit at the cost of a small loss of mass. A multilinear method, representing a compromise between linear and nonlinear methods, has been developed recently by Perumal (1992).

The Muskingum-Cunge is a viable alternative to the classical Muskingum method, particularly for the cases where hydrologic data (i.e., streamflow data) are not available, but where hydraulic data (cross-sectional data and channel slopes) can be readily ascertained. In many instances, the Muskingum-Cunge method is also an alternative to the more complex dynamic wave models, which lack robustness and have significant data requirements. The nonlinear features of the variable-parameter Muskingum-Gunge method makes it the method of choice in hydrologic flood routing.

This paper revisits the variable-parameter Muskingum-Cunge method of Ponce and Yevjevich (1978). The small but perceptible loss of mass is confirmed throughout a wide range of unit peak inflows, from 200 to 1000 cfs ft^-1 (18.58-92.9 m^-2s^-1). Furthermore, a slight improvement in mass conservation is realized by an alternative way of calculating the variable parameters.

2.  BACKGROUND

The Muskingum-Cunge method is a variant of the Muskingum method (Chow, 1959) developed by Cunge (1969) and documented in the Flood Studies Report (Natural Environment Research Council, 1975). Ponce and Yevjevich (1978) expressed the routing parameters of the Muskingum-Cunge method in terms of the Courant and cell Reynolds numbers, two physically and numerically meaningful parameters. In addition, they developed a nonlinear mode of calculating the parameters, thereby enhancing the method's applicability to real-world routing problems. A three-point method and an iterative four-point method were suggested as a way to vary the parameters as a function of local flow values. The method has been adopted by the most recent version (Version 4.0) of the US Corps of Engineers' HEC-1 model (1990).

The routing equation of the Muskingum-Cunge method defined in the typical four-point grid configuration is:

n + 1                 n + 1            n             n            Q j + 1     =   C0Qj       +  C1Qj   +   C2Qj + 1

(1)

in which j is a spatial index, n is a temporal index, and:

C0 = (-1 + C + D) / (1 + C + D)

(2)

C1 = (1 + C - D) / (1 + C + D)

(3)

C2 = (1 - C + D) / (1 + C + D)

(4)

are the routing coefficients, with C the Courant number, defined as follows:

C = c (Δt / Δx)

(5)

in which c is the wave cerelity, Δt is the time interval, Δx is the space interval, and D the cell Reynolds number, defined as follows:

D = q /(So c Δx)

(6)

in which q is the unit-width discharge and S_o is the bottom slope.

The wave celerity is defined as follows:

c = β (Q /A) = β (q / d )

(7)

in which β is the exponent of the rating, A is the flow area, and d is the flow depth.

The Muskingum-Cunge method matches the numerical diffusion of the discrete model with the physical diffusion of the analytical model. The advantage is that the routing results are independent of the grid specification, provided numerical dispersion is minimized. The numerical dispersion can be minimized by keeping the Courant number equal to or slightly greater than one (Cunge, 1969; Ponce and Theurer, 1982; Ferrick et. al., 1983).

3.  NUMERICAL EXPERIMENTS

In this paper, Thomas' (1934) classical problem was chosen to test the Muskingum-Cunge method under a wide range of flow conditions. The Thomas problem was chosen here to allow comparison with previous results (Ponce and Yevjevich, 1978). The original problem considered routing a sinusoidal flood wave with a 96-h period through a prismatic channel 500 miles long. A unit-width channel of baseflow q_b = 50 cfs ft^-1 (4.64 m² s^-1) and peak inflow q_pi = 200 cfs ft^-1 (18.58 m² s^-1) was specified. The bottom slope was set at 1 ft mile^-1, and the discharge-depth rating was the following:

q = 0.688 d 5/3

(8)

This amounts to a Manning's n = 0.0297. It can be shown that the 96-h sinusoidal flood wave satisfies the diffusion wave applicability criterion (Ponce et. al., 1978).

The following methods are considered here:

1. The constant-parameter method (CPMC), in which the routing parameters C and D are the same for all computational cells. They are based on an average unit-width discharge q_a calculated as:

   qa = (qb + qpi) / 2

   (9)

   
   

   The average celerity c_a is calculated with Eq. 7, using the discharge computed with Eq. 9.

2. The three-point variable-parameter method (VPMC3) (Ponce and Yevjevich, 1978), in which the routing parameters C and D for each computational cell are based on the average unit-width discharge and celerity at the three known grid points:

   n         n                n + 1                       qa =  (qj  +   q j + 1   +    q j     ) / 3

   (10)

   
   

   n         n              n + 1                       ca =  ( c j   +  c j + 1  +   c j      ) / 3

   (11)

   
   

3. The iterative four-point variable-parameter method (VPMC4) (Ponce and Yevjevich, 1978), in which the routing parameters C and D for each computational cell are based on the average unit-width discharge and celerity at the four grid points:

   n         n               n + 1        n + 1                qa =  (q j   +  q j + 1   +   q j      +   q j + 1    ) / 4

   (12)

   
   

   n         n               n + 1        n + 1                ca =  (c j   +  c j + 1   +   c j      +   c j + 1    ) / 4

   (13)

   
   

   To improve the convergence of the iterative procedure, the discharge q_{j + 1}^{n + 1} obtained with the three-point method (VPMC3) is used as a first guess of the iteration. The celerity c_{j + 1}^{n + 1} is calculated with Eq. 7, based on q_{j + 1}^{n + 1}. The iteration converges to a specified tolerance after a few trials.

4. A modified three-point variable-parameter method (MVPMC3), in which the routing parameters C and D for each computational cell are based on the average unit-width discharge at the three known grid points:

   n          n               n + 1                       qa =  (q j   +   q j   +  1  +  q j      ) / 3

   (14)

   
   

   Unlike the VPMC3, the average celerity c _a is calculated with Eq. 7, based on the discharge computed with Eq. 14.

5. A modified iterative four-point variable-parameter method (MVPMC4), in which the routing parameters C and D for each computational cell are based on the average unit-width discharge at the four grid points:

   n        n                 n + 1      n + 1                qa =  ( q j   +  q j + 1   +    q j    +   q j + 1    ) / 4

   (15)

   
   

   Unlike the VPMC4, the average celerity c _a is calculated with Eq. 7, based on the discharge q_a computed with Eq. 15. To improve the convergence of the iterative procedure, the discharge q_{j + 1}^{n + 1} obtained with the three-point method (MVPMC3) is used as a first guess of the iteration. The iteration converges to a specified tolerance after a few trials.

Two levels of spatial and temporal resolution were chosen:

1. Resolution level I, the grid specification used by Thomas (1934): Δx = 25 miles (40.22 km), and Δt = 6 h; and

2. Resolution level II, a finer grid specification used in this paper: Δx = 12.5 miles (20.11 km), and Δt = 3 h.

Three peak inflow to baseflow ratios q_pi /q_b were used:

1. q_pi /q_b = 4, used by Thomas (1934), Dooge (1973), and Ponce and Yevjevich (1978);

2. q_pi /q_b = 10; and

3. q_pi /q_b = 20.

These peak inflow to baseflow ratios encompass a wide range of practical values. With q_pi = 50 cfs ft^-1 (4.64 m²s^-1), the peak inflow range tested was 200 - 1000 cfs ft^-1 (18.58 - 92.9 m²s^-1).

---

4.  RESULTS

The mass conservation properties were assessed by integrating inflow and outflow hydrographs for the 500-mile reach. Table 1 shows peak outflow q_po, ratio of peak outflow to peak inflow q_po / q_pi, time-to-peak t_p, and mass conservation M for:

1. Two resolution levels: I and II;

2. Three peak inflow to baseflow q_pi / q_b ratios: 4, 10 and 20; and

3. Five methods: (a) CPMC; (b) VPMC3; (c) VPMC4; (d) MVPMC3; and (e) MVPMC4.

TABLE 1.  Summary of routing results.
Resolution level (1)	qpi /qb (2)	Method (3)	qpo (cfs ft-1) (4)	qpo /qpi (5)	tp (h) (6)	M (%) (7)
I	4	CPMC	176.231	0.881	126	100.000
		VPMC3	175.097	0.875	120	99.213
		VPMC4	175.860	0.879	120	99.464
		MVPMC3	175.437	0.877	120	99.334
		MVPMC4	176.084	0.880	120	99.559
I	10	CPMC	437.448	0.875	108	100.000
		VPMC3	435.592	0.871	102	97.180
		VPMC4	436.968	0.874	102	98.309
		MVPMC3	435.784	0.872	102	97.904
		MVPMC4	436.939	0.874	102	98.875
I	20	CPMC	876.675	0.877	96	100.000
		VPMC3	876.628	0.877	90	95.370
		VPMC4	878.236	0.878	90	97.444
		MVPMC3	876.160	0.876	90	96.700
		MVPMC4	877.786	0.878	90	98.441
II	4	CPMC	176.561	0.883	129	100.000
		VPMC3	174.146	0.871	123	99.330
		VPMC4	174.370	0.872	123	99.468
		MVPMC3	174.189	0.871	123	99.368
		MVPMC4	174.430	0.872	120	99.498
II	10	CPMC	438.666	0.877	105	100.000
		VPMC3	428.704	0.875	102	97.582
		VPMC4	429.937	0.860	99	98.224
		MVPMC3	429.094	0.858	102	97.847
		MVPMC4	430.580	0.861	99	98.429
II	20	CPMC	884.788	0.885	93	100.000
		VPMC3	866.356	0.866	87	95.943
		VPMC4	870.975	0.871	87	97.163
		MVPMC3	868.557	0.869	87	96.477
		MVPMC4	872.360	0.872	87	97.574
Note:  The peak outflows shown in Column 4 are those corresponding to the grid locations, and are not necessarily the actual peak outflows, which may lie in between.

The following conclusions are drawn from Table 1:

1. All five methods give approximately the same peak outflow q_po and time-to-peak t_p.

2. The ratio of peak outflow to peak inflow (q_po /q_pi) is approximately the same for all three peak-inflow-to-baseflow ratios. This suggests that wave diffusion is independent on the q_pi /q_b ratio.

3. The constant-parameter method (CPMC) conserves mass exactly. In contrast, the variable-parameter methods are subject to a small but perceptible loss of mass. The loss of mass is cumulative, and can be assessed quantitatively by routing through a very long reach. In this case, the routing of a sinusoidal hydrograph through a 500-mile reach produced mass losses ranging from less than 2.5% for MVPMC4 to less than 5% for VPMC3.

4. The loss of mass is greater for the three-point methods (VPMC3 and MVPMC3) than for the four-point methods (VPMC4 and MVPMC4).

5. The loss of mass is greater for the conventional methods (VPMC3 and VPMC4) than for the modified methods (MVPMC3 and MVPMC4).

6. The loss of mass increases with q_pi /q_b ratio, and does not appear to be strongly related to resolution level.

It should be noted that the mass conservation percentages shown in Column 7 of Table 1 are cumulative values for the 500-mile reach of the Thomas problem. A typical flood routing application would normally not consider such long reach without intervening lateral inflows which tend to mask the accuracy of the computation. Therefore, the percentages shown should be interpreted as an extreme or worst-case scenario.

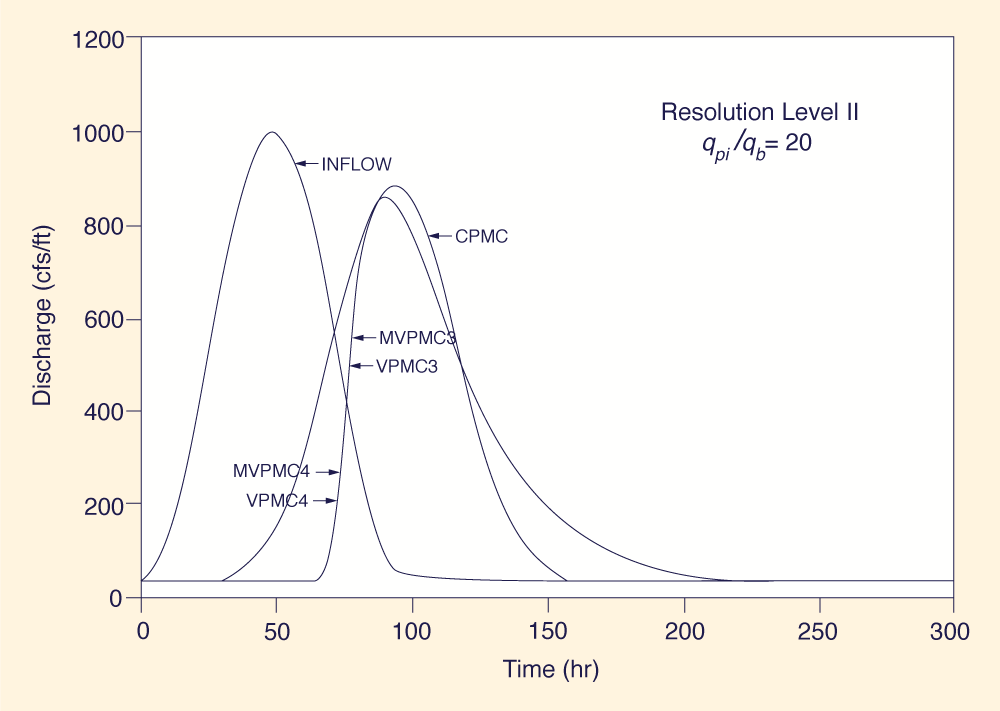
Figure 1 shows a set of flood hydrographs for resolution level II and peak inflow to baseflow q_pi /q_b = 20. It is seen that the constant-parameter method (CPMC) lacks the nonlinear tendency to steepening of the rising limb. (It is worth noting that overbank flows have the opposite tendency, i.e., the flattening of the rising limb). On the other hand, all four variable-parameter methods show steepening of the rising limb, coupled with a corresponding flattening of the receding limb.

Fig. 1.   Outflow hydrographs for Resolution Level II and peak inflow to baseflow ratio qpi /qb = 20.

---

5.  CONCLUSIONS

The modified variable-parameter methods MVPMC3 and MVPMC4 developed in this paper result in a definite improvement in mass conservation, as compared with the conventional methods VPMC3 and VPMC4 (Ponce and Yevjevich, 1978). The improvement may be more marked when using a wide range of realistic discharges. Otherwise, the small loss of mass does not appear to impose a significant drawback. It is the price to be paid to model the nonlinear features of a flood wave within the framework of the Muskingum-Cunge method.

---

REFERENCES

Chow, V. T., 1959. Open-Channel Hydraulics. McGraw-Hill, New York.

Cunge, J. A., 1969. On the subject of a flood propagation computation method (Muskingum method). J. Hydraul. Res., 7(2) 205-230.

Dooge, J. C. I., 1973. Linear theory of hydrologic systems. U.S. Dep. Agric. Tech. Bull., 1468, 327 pp.

Ferrick, M. G., Bilmes, J. and Long, S. E., 1983. Modeling rapidly varied flow in tailwaters. Water Resour. Res., 20(2): 271-289.

Natural Environment Research Council, 1975. Flood Studies Report, Vol. III. Natural Environment Research Council, London.

Perumal, M., 1992. Multilinear Muskingum flood routing method. J. Hydrol., 133: 259-272.

Ponce, V. M. and Theurer, F. D., 1982. Accuracy criteria in diffusion routing. J. Hydraul. Div., ASCE., 108 (HY6): 747-757.

Ponce, V. M. and Yevjevich, V., 1978. Muskingum-Cunge method with variable parameters. J. Hydraul. Div. ASCE, 104(HY12): 1663-1667.

Ponce, V. M., Li, R-M. and Simons, D. B., 1978. Applicability of knematic and diffusion models. J. Hydraul. Div. ASCE, 104(HY3): 353-360.

Thomas, H. A., 1934. The hydraulics of flood movement in rivers. Eng. Bull., Carnegie Inst. of Technology, Pittsburgh, PA.

US Army Corps of Engineers, 1990. HEC-1, flood hydrograph package: User's manual, version 4, 1990. US Army Corps of Engineers, Hydrologic Engineering Center, Davis, CA.

---