1. INTRODUCCIÓN Las ondas de rollo pueden ocurrir en un régimen de flujo de superficie libre inestable, es decir, cuando el número de Vedernikov excede el valor de 1. El régimen de flujo puede ser laminar o turbulento. En el régimen laminar, un ejemplo de ondas de rollo es el flujo pulsante que a menudo se observa en el pavimento, en cuencas urbanas empinadas, inmediatamente después de lluvias intensas. En el régimen de flujo turbulento, las ondas de rollo pueden requerir una condición de frontera específica para su inicio. El número de Vedernikov V > 1 (Vedernikov 1945, 1946) es la condición necesaria para la formación de ondas de rollo. La existencia de este criterio fue confirmada por Craya (1952) e Iwasa (1954). Utilizando la teoría de la estabilidad lineal, Ponce y Simons (1977) confirmaron el criterio de Vedernikov para la fricción turbulenta de Chezy en canales hidráulicamente anchos. Además, Ponce y Simons identificaron la escala de las perturbaciones bajo las cuales es más probable que se desarrollen las ondas de rollo. Brock (1967) estudió experimentalmente la propagación de ondas de rollo utilizando un canal de laboratorio. Brock midió las profundidades de las crestas y los períodos de las ondas, para la fricción turbulenta de Chezy en canales hidráulicamente anchos, en una amplia gama de condiciones de flujo.
El objetivo de este artículo es utilizar los datos de Brock (1967) para confirmar la validez de la teoría de Ponce y Simons (1977). Los números de onda experimentales, calculados a partir de los períodos de onda medidos por Brock, se comparan con los números de onda predecidos por la teoría. 2. NÚMERO DE VEDERNIKOV El número de Vedernikov se define como sigue (Chow 1959):
en la cual x = exponente del radio hidráulico R en la relación u = f(R); γ = factor de forma de la sección transversal; y F = número de Froude. El parámetro x es definido como sigue:
en la cual b = exponente del número de Reynolds R en la ley f = α(R)-b, en la cual f = factor de fricción de Darcy-Weisbach. El parámetro b varía en el rango 0-1, con b = 0 aplicable para la fricción turbulenta de Chezy; y con b = 1 aplicable al flujo laminar. El factor de forma γ es definido como sigue:
en la cual P = perímetro mojado; y A = área de flujo. El factor de forma γ varía en el rango 0-1, 3. TEORÍA DE LA FORMACIÓN DE ONDAS DE ROLLO
El análisis de estabilidad lineal de Ponce y Simons (1977) expresa las características de propagación de las ondas en aguas poco profundas en términos de: (1) El número de Froude F del flujo uniforme permanente; y (2) un número de onda adimensional que caracteriza el componente no permanente del movimiento. El número de Froude se define como F = uo / (gdo)1/2; en el cual
Las características de propagación de las ondas en aguas poco profundas son: (1) la celeridad de onda relativa adimensional cr; y (2) el decremento logarítmico δ. La celeridad de onda relativa adimensional cr = (c - uo) / uo, en la cual c = celeridad de onda. El decremento logarítmico δ es una medida de la tendencia de la perturbación a atenuarse o amplificarse durante la propagación. Las expresiones teóricas para la celeridad de onda adimensional y el decremento logarítmico se repiten aquí (Ponce y Simons 1977). La celeridad de onda relativa adimensional es:
en la cual:
y
El decremento logarítmico de la onda superficial que se propaga aguas abajo es el siguiente:
4. RESULTADOS
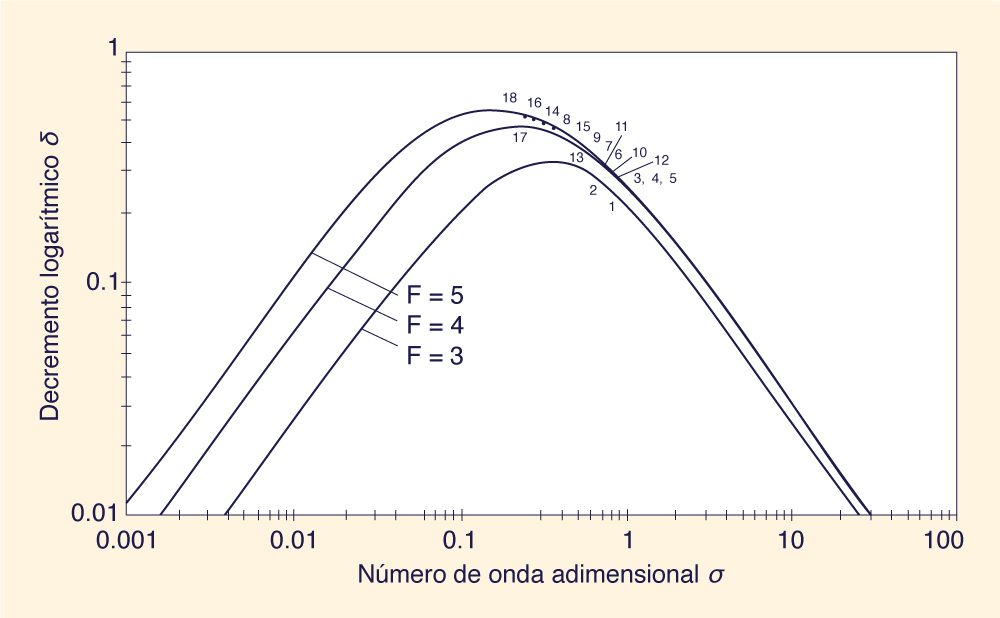
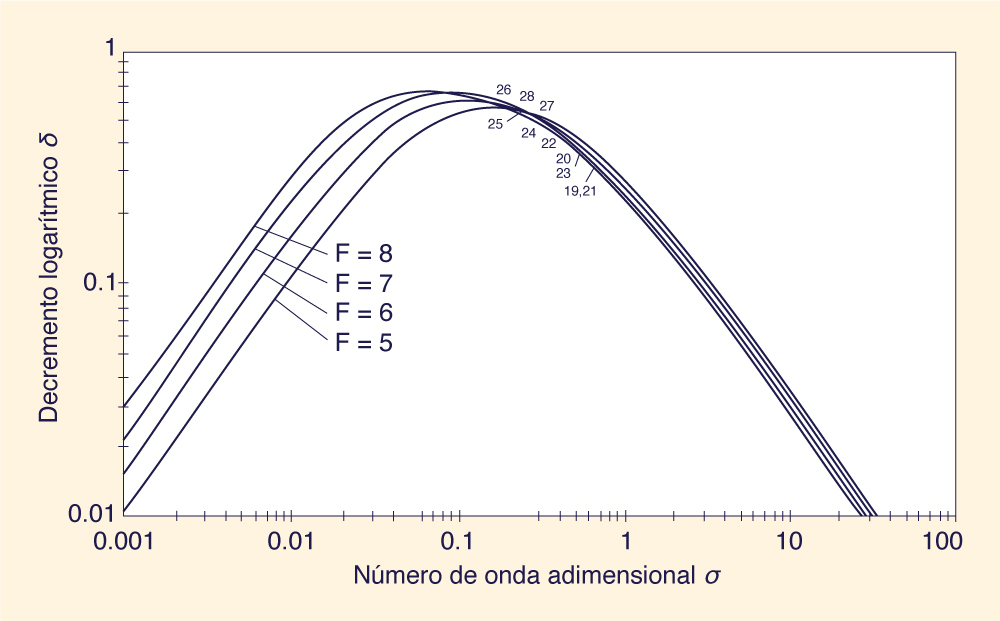
Los datos de Brock (1967) se muestra en la Tabla 1: (1) Profundidad normal (es decir, flujo uniforme permanente) do; (2) pendiente de fondo So; (3) celeridad de onda c; y (4) período de onda T, para 28 casos de prueba incluidos en el estudio de Brock. La profundidad normal y la pendiente del fondo se utilizaron para calcular la longitud del canal de referencia Lo = do/So. La celeridad de onda y el período de onda se usaron para calcular la longitud de onda L = cT. El número de onda adimensional se define de la siguiente manera (Ponce y Simons 1977): σ = (2π / L)Lo. Suponiendo que la celeridad de la onda de rollo sea aproximadamente igual a la celeridad de la onda de inercia c = uo + (gdo)1/2, el número de Froude se estimó de la siguiente manera: F = c / (gdo)1/2 - 1
Las curvas sólidas de las Figs. 1 y 2 muestran el decremento logarítmico δ versus el número de onda adimensional σ, (7), para el rango de números de Froude adecuado para este estudio.
5. RESUMEN Utilizando los datos de laboratorio de Brock (1967), se ha presentado una verificación experimental de la teoría de la formación de ondas de rollo (Ponce y Simons 1977). Los resultados muestran que los números de onda adimensionales correspondientes a las ondas de rollo, documentadas por el estudio de Brock, se localizan cerca del pico de la relación del decremento logarítmico δ versus el número de onda adimensional σ. El análisis confirma que es más probable que se formen ondas de rollo para valores grandes positivos del decremento logarítmico (δ > 0.2), ubicados dentro de una estrecha banda central de números de onda adimensionales.
APÉNDICE I. BIBLIOGRAFÍA
Brock, R. R. 1967. "Development of roll waves in open channels." Rep. No. KH. R-16, W. M. Keck Laboratory of Hydraulics and Water Resources, California institute of Technology, Pasadena. Calif.
Chow, V. T. 1959. Open-channel hydraulics, McGraw-Hill, New York, N.Y.
Craya, A. 1952. "The criterion of the possibility of roll wave formation." Gravity Waves, National Bureau of Standards Circular No. 521, National Bureau of Standards, Washington, D.C., 141-151.
lwasa, Y. 1954. "The criterion for the instability of steady uniform flows in open channels." Memoirs of the Faculty of Engineering, Kyoto University, Kyolo,Japan, 16(6),264-275.
Liggett, J. A. 1975. "Stability - Chapter 6," Unsteady flow in open channels, Vol. 1, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Fort Collins, Colo., 259-281.
Mayer, P. G. W. 1957. "A study of roll waves and slug flows in inclined open channels," PhD dissertation, Cornell University, Ithaca, N.Y.
Ponce, V. M., y D. B. Simons. 1977. "Shallow wave propagation in open channel flow." J. Hydr. Div., ASCE, 103(12), 1461-1476.
Ponce, V. M. 1991. "New perspective on the Vedernikov number," Water Resour. Res., 27(7), 1777-1779.
Vedernikov, V. V. 1945. "Conditions at the front of a translation wave disturbing a steady motion of a real fluid," U.S.S.R. Academy of Sciences Comptes Rendus (Doklady), 48(4), 239-242.
Vedernikov, V. V. 1946. "Characteristics features of a liquid flow in an open channel." U.S.S.R. Academy of Sciences Comptes Rendus (Doklady), 52(3), 207-210.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 221125 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |