|
|
|
CAPÍTULO 11: FLUJO NO PERMANENTE RÁPIDAMENTE VARIADO |
11.1 ONDAS SUPERFICIALES
|
|
Las ondas superficiales son características del flujo no permanente [en
canales] las cuales ocurren típicamente bajo números de Froude altos.
La Figura 11-1 muestra una onda superficial en el río Hassayampa, cerca de Morristown,
Arizona (Phillips y Ingersoll, 1998). La perturbación es
una onda que se propaga lentamente en dirección aguas abajo, indicando
flujo en un canal
aluvial en condiciones de régimen superior
Fig. 11-1 Vista aguas arriba del río Hassayampa, cerca de Morristown, Arizona,
|
|
La Figura 11-3 muestra el río Santa Catarina, en Monterrey, Nuevo León, México, durante el paso del Huracán Gilberto, el 17 de septiembre de 1988. Las grandes ondas superficiales que se observan son una indicación de flujos con altos números de Froude, los cuales muy probablemente prevalecieron durante el paso de la avenida.
Fig. 11-3 El río Santa Catarina, en Monterrey, Nuevo León, México, durante el paso |
11.2 OLEADAS
|
|
Las oleadas son perturbaciones creadas por cierres repentinos
de compuertas, o por cambios bruscos en el
nivel de la superficie del agua o la profundidad de flujo.
Típicamente, una oleada es corta y
no se atenúa fácilmente, trasladándose una distancia considerable a lo largo del canal.
Las oleadas se pueden evitar si la apertura de la compuerta se hace lentamente, minimizando así
la posibilidad de cambios bruscos en el nivel de la superficie del agua y/o profundidad de flujo.
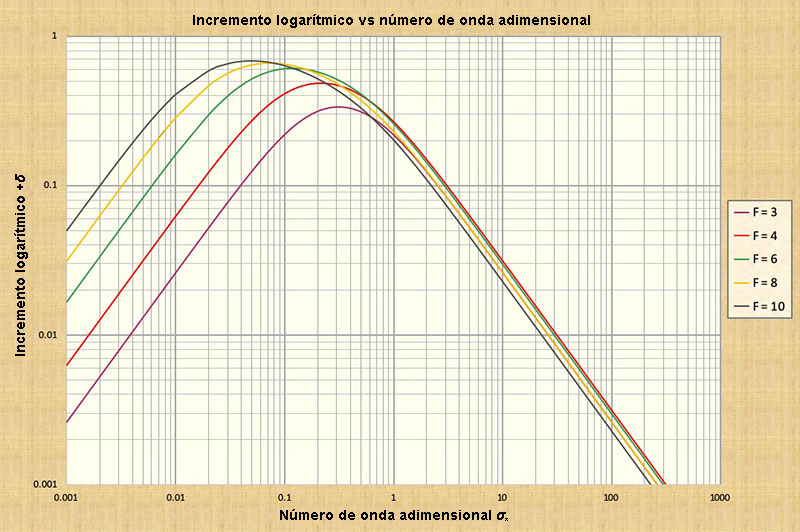
La atenuación de la oleada aumenta en cuanto disminuye
el número de onda adimensional, de aquél correspondiente a una
onda dinámica verdadera (con celeridad constante y atenuación nula), a aquél correspondiente
a una onda dinámica mixta (con celeridad variable y atenuación apreciable)
Fig. 11-4 La celeridad relativa adimensional en función del número de onda adimensional |
Basando el cálculo en el criterio anterior, una primera aproximación del tiempo de apertura To de la compuerta para disminuir la posibilidad de una oleada es (Ponce et al., 1999):
k uo | (11-1) |
en la cual uo = velocidad de flujo, So = pendiente de fondo, g = aceleración de la gravedad, y k = una constante que varía con el número de Froude como se muestra en la Tabla 11-1.
| ||||||||||||||
11.3 CHOQUES CINEMÁTICOS
|
|
Los choques cinemáticos son ondas cinemáticas que se han empinado hasta convertirse prácticamente en una pared de agua, con la cara de la onda en forma casi vertical. En la realidad, el choque no es una discontinuidad perfecta; sin embargo, su espesor es relativamente pequeño en comparación con la escala de la perturbación (Lighthill and Whitham, 1955).
Las ondas cinemáticas se trasladan aguas abajo y pueden empinarse o aplanarse, dependiendo de su interacción con la sección transversal. Solamente las ondas cinemáticas más empinadas pueden convertirse en choques cinemáticos. Nótese que mientras que las ondas cinemáticas constituyen un flujo gradualmente variado, los choques cinemáticos no lo son necesariamente.
El desarrollo de un choque cinemático es una función de las siguientes condiciones (Ponce y Windingland, 1985):
-
El tipo de onda
Cuanto más cinemática es una onda (es decir, menor el número de onda adimensional), menor será su tendencia a atenuarse y, por lo tanto, mayor será su tendencia a empinarse.
La relación de flujo base a flujo pico
Cuanto menor es la relación de flujo base a flujo pico, mayor será la tendencia de la onda a empinarse. Este comportamiento se debe a la no linearidad de la onda (los flujos mayores, dentro del banco, se trasladan con celeridades mayores).
El régimen de flujo
Los flujos con números de Froude altos tienen una menor tendencia a la atenuación; por lo tanto, cuanto mayor sea el número de Froude, menor será la atenuación. En el límite, al aproximarse el flujo al número de Vedernikov V = 1 (es decir, F = 2 para la fricción de Chezy en canales hidráulicamente anchos), el flujo llega a ser neutralmente estable, reduciéndose la atenuación a cero.
El tipo de sección transversal
Los canales hidráulicamente anchos, para los cuales el exponente de la curva de gasto es
β = 1.5 (bajo la fricción de Chezy), tienen una mayor tendencia a empinarse que los canales triangulares, para los cuales β = 1.25. Los canales inherentemente estables, para los cualesβ = 1, no tienen ninguna tendencia a empinarse (Véase la Tabla 10-3 para otros valores de β).
Por lo tanto, los choques cinemáticos se desarrollan en los casos en los cuales se presentan: (a) una onda cinemática, (b) un río o corriente efímera (es decir, con flujo base inexistente), (c) una velocidad de flujo alta (es decir, una avenida), y (d) un canal hidráulicamente ancho. Éste sería el caso de una tormenta de proporciones considerables en una región predominantemente semiárida, la cual tendería a concentrar el flujo rápidamente a través de un cañón amplio y de paredes casi verticales.
El 26 de Julio de 1981 se produjo una avenida muy súbita en el arroyo Tanque Verde, un afluente del río Santa Cruz, en el este del estado de Arizona, EE.UU. La avenida produjo una onda, la cual fue con toda probabilidad un choque cinemático, A pesar de que la magnitud [frecuencia] de la avenida fue sólo de 2 años de período de retorno, causó la muerte de ocho personas. A juzgar por las narrativas de los sobrevivientes, la rapidez de aproximación de la onda de avenida fue tal que se asemejaba a un "muro de agua" (Hjalmarson, 1984).
Los choques cinemáticos han sido observados con cierta frecuencia en los cálculos numéricos de flujo de superficie. Cabe mencionar que estos cálculos son muy propicios para el desarrollo del choque cinemático (Kibler y Woolhiser, 1970). La presencia frecuente del choque se atribuye a la regularidad espacial prescrita, la cual es necesaria para que el problema pueda ser resuelto de una manera viable.
11.4 ONDAS DE ROLLO
|
|
Las ondas de rollo se desarrollan en flujo en canales cuando
el número de Vedernikov V > 1
(
El número de Vedernikov se define como la relación de la celeridad relativa de la onda cinemática a la celeridad relativa de la onda dinámica (Ponce, 1991):
(β - 1) u | (11-2) |
en la cual β = exponente de la curva de gasto
(relación descarga-área) (Ec. 10-52),
u = velocidad media, h = profundidad de flujo, y
g = aceleración de la gravedad.
Las ondas de rollo se producen cuando la celeridad relativa de la onda
cinemática supera a la celeridad relativa de la onda dinámica.
Dado que la masa transporta ondas cinemáticas, y
la energía transporta ondas dinámicas (verdaderas),
las ondas de rollo se producen en el umbral en el cual
la masa y la energía están siendo transportadas a la misma velocidad.
En la práctica, las
ondas de rollo se producen en canales artificiales de fuerte pendiente
cuando el número de Vedernikov
Fig. 11-5 Ondas de rollo en un canal de irrigación de pendiente fuerte, |
La condición
| Video de ondas de rollo en La Paz, Bolivia (2014). |
|
Un ejemplo curioso y un tanto extremo de ondas de rollo en un canal urbano empinado se muestra en el video de un evento en el río Huayñajahuira, en La Paz, Bolivia, el 25 de febrero de 2016, a las 5:30 pm.
| Video de ondas de rollo en el Río Huayñajahuira, La Paz, Bolivia (2016). |
11.5 ONDAS DE MAREA
|
|
Las ondas de marea son características del flujo no permanente rápidamente variado, las cuales ocurren en ciertos ríos en la proximidad de sus estuarios. Las ondas se producen en estuarios que poseen un gran rango de marea (variación del nivel), en las fechas cercanas a los equinoccios (20 de marzo y 22 de septiembre). El hecho de que la onda de marea sea capaz de trasladarse aguas arriba del estuario, y eventualmente convertirse en una onda visible, de profundidad finita, depende en gran medida de la geometría de la sección transversal del estuario. Las grandes ondas de marea, de alturas mayores de 2 m, son más propensas a formarse en canales hidráulicamente anchos, de profundidad casi constante, y de fricción relativamente baja.
|
Se han observado grandes ondas de marea en el río Araguari, Amapá, Brasil, y en otros estuarios en ciertas regiones a nivel global. Chow (1959) describió una onda de marea en la localidad de Haining, en el río Chien Tang, China. El frente de onda viajó a gran velocidad y fué observado a través de una longitud de 11 km (Fig. 11-8). La onda alcanzó una altura final de 8.4 m en un total de 30 minutos. El ancho del río en el punto de observación fue de aproximadamente 1.6 km.
|
11.6 FLUJOS HIPERCONCENTRADOS
|
|
Los flujos hiperconcentrados de sedimentos son acumulaciones repentinas de escurrimiento que contienen grandes cantidades de partículas sólidas, generalmente de tamaños correspondientes a cantos rodados y aún mayores. Los flujos hiperconcentrados se trasladan aguas abajo a gran velocidad, destruyendo todo a su paso y poniendo en peligro la vida y la propiedad (Fig. 11-9).
|
Los flujos hiperconcentrados son inducidos por lluvias intensas, pero también pueden ser provocados por terremotos. Por ejemplo, en el Sur de California, a lo largo de la base de las montañas de San Gabriel, al este de Los Ángeles, los flujos hiperconcentrados inducidos por la lluvia se presentan con regularidad. Los factores que conducen a la formación de estos flujos hiperconcentrados son:
El tectonismo
Las montañas de San Gabriel se cuentan entre las más tectónicamente activas de los Estados Unidos (Fig. 11-10). El tectonismo produce una pendiente pronunciada, lo que aumenta la fuerza de gravedad y consecuentemente, el potencial de erosión.

Wikimedia Commons Fig. 11-10 Las montañas de San Gabriel, en el Sur de California, EE.UU.
El ecosistema de chaparral
El ecosistema de chaparral es endémico en la región, sobreviviendo las largas sequías mediante adaptaciones singulares que consisten en el recubrimiento superficial de las hojas con una cera protectora, la cual contribuye a reducir notablemente la evapotranspiración (McPhee, 1989)
(Fig. 11-11) .
Fig. 11-11 Ecosistema de chaparral, Tierra del Sol, Condado de San Diego, California.
El viento
La región alberga los reconocidos vientos de Santa Ana, los cuales son generalmente muy secos y fuertes, pudiendo alcanzar velocidades de más de 60 km por hora, manteniendo así un clima propicio para el fuego.
El fuego
Después de una larga sequía, el fuego sigue al viento, particularmente cuando el bosque de chaparral ha permanecido sin quemarse por más de 30 años (Fig. 11-12).

Fig. 11-12 Secuela del incendio Shockey, el 27 de Septiembre de 2012,
en Tierra del Sol, Condado de San Diego, California.La lluvia
La lluvia sigue al incendio, debido al exceso de partículas de ceniza en el aire, lo cual promueve la coalescencia y la consecuente formación de precipitación.
Las pendientes empinadas, cubiertas con bosques de chaparral, sujetas a la secuencia de viento, fuego, y lluvia, son los factores que desencadenan los flujos hiperconcentrados de sedimentos en la región del Sur de California. Durante el incendio, las partículas de cera [contenidas en la hojas] se vaporizan en la superficie, recondensándose a un espesor que varía de 10 a 50 mm, por debajo del cual el suelo es hidrofóbico, es decir, no humedecible. La acumulación del escurrimiento causado por lluvias muy intensas, superiores a 25 mm por hora, por debajo de la superficie y por encima de la capa no humedecible, conduce al arrastre de grandes cantidades de sedimento que eventualmente llegan a constituir los flujos hiperconcentrados.
Un flujo hiperconcentrado normal inducido por una lluvia fuerte en el Sur de California puede remover de
Los flujos masivos hiperconcentrados de sedimentos (deslizamientos o aludes) suelen ser provocados
por terremotos. Tal fue el caso del deslizamiento del Nevado Huascarán,
el 30 de Mayo de 1970, en el Perú, que sepultó la ciudad de
Yungay, provocando la muerte de más de 20,000 personas
Fig. 11-13 Ruinas de la iglesia en la plaza central de Yungay, Ancash, Perú,
sepultada |
11.7 LAHARES
|
|
Los lahares son flujos hiperconcentrados de sedimentos provocados por el deshielo que sigue a una erupción volcánica, con la posterior fusión repentina de la cobertura glacial. La palabra lahar se originó en Indonesia, donde el fenómeno se repite con regularidad. Los lahares tienen la consistencia, viscosidad, y aproximadamente la misma densidad que el hormigón: Fluído cuando está en movimiento y sólido cuando cesa de moverse (Fig. 11-14).
Fig. 11-14 Un lahar en el río Bajo Sacobia, Islas Filipinas,
|
Los lahares pueden ser masivos y mortales, como lo demuestra la erupción del volcán Nevado del Ruiz, en Colombia, el 13 de noviembre de 1985. En esa oportunidad, cuatro lahares descendieron por los flancos del volcán. El más grande de ellos prácticamente destruyó la ciudad de Armero, sepultándola bajo 5 m de lodo y escombros, causando la muerte de más del 75% de sus 28,700 habitantes (Fig. 11-15).
Fig. 11-15 La localidad de Armero, en Caldas/Tolima, Colombia, sepultada |
PREGUNTAS
|
|
¿Qué formas de fondo del río se desarrollan bajo el régimen superior en el flujo en un canal aluvial?
¿Cuándo se forman las oleadas en el flujo en canales?
¿Qué es un choque cinemático?
¿Qué condiciones son necesarias para que una onda cinemática se transforme en un choque cinemático?
¿Cuándo se desarrollan las ondas de rollo?
¿Las ondas de rollo siempre se desarrollan en canales de fuerte pendiente?
¿Dónde son las ondas de marea más propensas a formarse?
¿Qué es un flujo hiperconcentrado de sedimentos?
¿Qué condiciones son propicias para el desarrollo de flujos hiperconcentrados de sedimentos en la región del Sur de California?
¿Qué es un lahar?
PROBLEMAS
|
|
-
Calcular el tiempo de apertura de una compuerta en un canal, dadas las siguientes condiciones de flujo: profundidad
do = 1.2 m, velocidad uo = 1.5 m/s, y pendiente de fondo So = 0.001. -
Un canal dado tiene un factor de fricción modificado de Darcy-Weisbach f = 0.0035. La pendiente de fondo es So = 0.014. Determinar si esta condición de flujo es estable para la fricción de Chezy en un canal hidráulicamente ancho.
BIBLIOGRAFÍA
|
|
Brock, R. R. 1967. Development of roll waves in open channels. ReportE No. KH-R-16, W. M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California,
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York.
Cornish, V. 1907. Progressive waves in rivers. The Geographical Journal. Vol. 29, No. 1, Enero, 23-31.
Craya, A. 1952. The criterion for the possibility of roll-wave formation. Gravity Waves, Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.
Hjalmarson, H. W. 1984. Flash flood in Tanque Verde Creek, Tucson, Arizona. Journal of Hydraulic Engineering, Vol. 110, No. 12, 1841-1852.
Jarrett, R. D. 1984. Hydraulics of high-gradient streams. Journal of Hydraulic Engineering, Vol. 110, No. 11, 1519-1539.
Kibler, D. F., y D. A. Woolhiser. 1970. The kinematic cascade as a hydrologic model. Hydrology Paper No. 39, Colorado State University, Ft. Collins, Colorado.
Lighthill, M. J., y G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
McPhee, J. 1989. The Control of Nature. Farrar Straus Giroux, Nueva York.
Ponce, V, M., y D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, Abril, 600-611.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, Julio.
Ponce, V, M., y M. P. Maisner. 1993. Verification of theory of roll wave formation. Journal of Hydraulic Engineering, ASCE, Vol. 119, No. 6, Junio, 768-773.
Ponce, V, M., Y. R. S.Rao, y N. M. Mansury. 1999. Time of opening of irrigation canal gates. Journal of Hydraulic Engineering, ASCE, Vol. 125, No. 9, Septiembre, 979-980.
Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.
Phillips, J. V., y T. L. Ingersoll. 1998. Verification of roughness coefficients for selected natural and constructed stream channels in Arizona. U.S. Geological Survey Professional Paper 1584, Washington, D.C.
Simons, D. B., y E. V. Richardson. 1966. Resistance to flow in alluvial channels. U.S. Geological Survey Professional Paper 422-J, Washington, D.C.
| http://hidraulicadecanales.sdsu.edu |
|
170820 22:30 |