|
|
|
CAPÍTULO 9: FLUJO PERMANENTE RÁPIDAMENTE VARIADO |
9.1 VERTEDERO DE PARED DELGADA
|
|
La diferencia entre el flujo rápidamente variado y el gradualmente variado (Capítulo 7) es que el primero presenta una mayor curvatura en las líneas de corriente. En casos extremos, el flujo puede casi romperse, lo cual resulta en un alto grado de turbulencia y pérdida de carga.
Las siguientes características describen el flujo rápidamente variado:
-
La curvatura de las líneas de corriente es tan pronunciada que no se puede suponer una distribución hidrostática de presiones.
-
A diferencia del flujo gradualmente variado, los cambios en las variables ocurren en una distancia relativamente corta (Fig. 9-1).
-
La fricción en el perímetro es pequeña en comparación con las otras fuerzas y, por lo tanto, puede despreciarse.
-
Las características del flujo son fijadas por la geometría del perímetro, la cual es usualmente rígida.
-
Los coeficientes de distribución de velocidades α y β son mucho mayores que uno (1) y no pueden ser determinados con precisión.
-
Las zonas de separación, los remolinos y los rodillos tienden a complicar el patrón del flujo, el cual a menudo se encuentra dentro de zonas de separación.
No existe aún una solución teórica para el flujo rápidamente variado; por lo tanto, en muchas aplicaciones se utilizan relaciones empíricas.
|
El vertedero de pared delgada
El vertedero de pared delgada es un dispositivo para la medición de flujo en canales (Capítulo 4). Además, es la forma más simple de un vertedero de demasías. El perfil del vertedero se puede diseñar de tal manera que coincida con la forma de la superficie inferior de la napa. La forma de la napa puede ser calculada usando el principio del proyectil (Chow, 1959) (Fig. 9-2).
|
De acuerdo con este principio, el componente de velocidad horizontal del flujo es constante, y la única fuerza que actúa sobre la napa es la fuerza de gravitación. En el tiempo t, una partícula de agua en la superficie inferior de la napa se trasladará una distancia horizontal x (desde la cara del vertedero) igual a:
x = vo t cos θ | (9-1) |
Al mismo tiempo, la partícula se desplazará una distancia vertical y igual a:
y = - vo t sin θ + (1/2) g t 2 + C' | (9-2) |
en la cual g = aceleración de la gravedad, y C' es el valor de y correspondiente a x = 0. La constante C' se puede tomar como la distancia vertical entre el punto más alto de la napa y la elevación de la cresta.
Eliminando t de las Ecs. 9-1 y 9-2:
y x x | (9-3) |
en el cual:
g H | (9-4) |
| (9-5) |
C' | (9-6) |
Suponiendo un valor T para el espesor vertical de la napa, se puede añadir un término adicional a la Ec. 9-5 para obtener la ecuación de la napa:
y x x | (9-7) |
en la cual D = T /H .
Descarga del vertedero de pared delgada
Una fórmula común para la descarga sobre un vertedero de pared delgada es la siguiente:
Q = C L H 3/2 | (9-8) |
en la cual C = coeficiente de descarga, L = longitud efectiva de la cresta del vertedero, y H = altura medida por encima de la cresta, excluyendo la carga de velocidad. El Capítulo 4 muestra coeficientes de descarga para varios tipos de vertederos de pared delgada.
9.2 PERFIL DE LA CRESTA DEL VERTEDERO
|
|
La forma o perfil del vertedero que se muestra en la Fig. 9-3 se conoce como ogee o conopial, la cual se asemeja a una S, con dos arcos opuestos, de modo que los extremos son aproximadamente paralelos. En la práctica, no obstante la forma del vertedero, se pueden desarrollar presiones negativas en un vertedero ogee. Las presiones negativas excesivas pueden provocar daños por cavitación y, por lo tanto, deben ser minimizadas o controladas.
|
|
El Cuerpo de Ingenieros del Ejército de EE.UU. ha desarrollado varios perfiles estándar en su estación experimental (Waterways Experiment Station). A estos perfiles, los cuales se muestran en la Fig. 9-4, se les conoce como los perfiles del vertedero WES estándar.
|
Los perfiles WES están descritos por la siguiente ecuación:
X n = K Hd n-1 Y | (9-9) |
en la cual X y Y son las coordenadas del perfil de la cresta, con el origen de coordenadas en el punto más alto (de la cresta); Hd = carga de diseño, excluyendo la carga de velocidad en el flujo inmediatamente aguas arriba, y K y n son parámetros que dependen de la pendiente de la cara aguas arriba del vertedero. La Tabla 9-1 muestra los valores de K y n. Se pueden calcular los valores intermedios por interpolación.
| Tabla 9-1 Valores de K y n (Ec. 9-9). | ||||||||||||||
| Pendiente de la cara aguas arriba | K | n
| Vertical
| 2.000
| 1.850
| 3 V : 1 H
| 1.936
| 1.836
| 3 V : 2 H
| 1.939
| 1.810
| 3 V : 3 H
| 1.873
| 1.776
| |
En algunos casos, el paramento aguas arriba puede ser diseñado con receso, como muestran las líneas punteadas de la Fig. 9-4. Este detalle de diseño no afectará la forma de la cresta, siempre y cuando la modificación comience por debajo del origen, a por lo menos la mitad de la carga He. Por debajo de esta profundidad, las velocidades verticales son pequeñas y el efecto correspondiente en el perfil de la napa es despreciable.
Para los perfiles WES, la descarga sobre el vertedero es:
Q = C L He 3/2 | (9-10) |
en la cual He = carga de energía total sobre la cresta, incluyendo la
carga de velocidad inmediatamente aguas arriba. Los ensayos en modelos han demostrado que
el efecto de la velocidad de aproximación es despreciable cuando
la altura h del vertedero es mayor de 1.33 Hd,
en la cual
En vertederos de poca altura, para los cuales h/Hd < 1.33,
la velocidad inmediatamente aguas arriba tendrá un efecto apreciable sobre la descarga y,
por lo tanto, sobre el perfil de la napa.
La Figura 9-5 muestra el
efecto de la velocidad inmediatamente aguas arriba en la relación entre
Para una cara aguas arriba no vertical, C se multiplica por el
factor de corrección que se muestra en la parte superior izquierda de la
|
|
Vertedero WES: Ejemplo de diseño
Determinar la elevación de la cresta y el perfil del
vertedero (la forma del vertedero WES estándar) para el caso de una
cara vertical aguas arriba y longitud de cresta L = 250 pies.
El caudal de diseño es de
Solución
|
Vertederos de tipo conopial (ogee)
La Figura 9-7 muestra varios vertederos conopiales.
Este tipo de vertedero se utiliza en presas altas, ya que
su coeficiente de descarga
(C = 4.03 en unidades acostumbradas en EE.UU. y
|
|
|
La Figura 9-8 muestra dos vertederos de cresta ancha. El vertedero de demasías de 8000 pies de largo del Lago de Conservación Boerasirie, en Guyana, mostrado en la Fig. 9-8 (a), ha sido diseñado con un coeficiente de descarga que varía de C = 1.45 a nivel de cresta a C = 1.78 para la carga de diseño Hd = 0.215 m (coeficiente de descarga en unidades SI). La presa Valle Grande, en Cuajone, Perú, mostrada en la Fig. 9-8 (b), contiene un embalse fuera del arroyo, con un área de drenaje relativamente pequeña; por lo tanto, no se esperan mayores inundaciones y el vertedero de cresta ancha se considera suficiente para pasar la descarga de diseño.
|
|
Vertederos tipo laberinto
El vertedero tipo laberinto se utiliza para aumentar la longitud efectiva de la cresta, en caso de que la posibilidad de riesgo hidrológico sea grande. La Figura 9-9 muestra tres ejemplos de vertederos tipo laberinto. El laberinto funciona bien para la carga de diseño; sin embargo, para cargas superiores a la de diseño, la longitud efectiva se reduce eventualmente a la longitud real y el laberinto deja de proporcionar la ventaja deseada.
|
|
Fig. 9-9 (c) Presa Ute, Nuevo México. |
Un vertedero fusible es un terraplén diseñado para fallar de una manera predecible y controlada cuando el flujo excede la capacidad normal del vertedero, y por lo tanto se requiere de una salida práctica (Pugh y Gray, 1984). El diseño de los vertederos fusible para las presas Bartlett y Horseshoe, en el Río Verde, Arizona, se ha llevado a cabo de acuerdo con la práctica del U.S. Bureau of Reclamation. El vertedero fusible para la presa Bartlett cuenta con una estructura resistente a la erosión suficiente para un flujo de 10,100 m3/s. Las tres secciones erosionables del terraplén están diseñadas para operar en secuencia. El vertedero de fusible de la presa Horseshoe está diseñado para pasar 6,850 m3/s a través de tres aperturas de 44 a 52 m de largo y 6.0 m a 7.9 m de altura.
|
Otras características hidráulicas de vertederos incluyen compuerta de jebe (empaque). (Fig. 9-11), vertederos con salto de ski (Fig. 9-12), y estructuras de disipación (Fig. 9-13).
|
|
Fig. 9-13 Estructuras de disipación de flujo, presa Gallito Ciego, La Libertad, Perú. |
En febrero de 2017, los dos vertederos, el de control de inundaciones y el de emergencia, de la Presa Oroville, en el norte de California, Estados Unidos, fallaron luego de que 325 mm de precipitación cayeran entre el 6 y el 10 de febrero en la cuenca del Río Feather. La secuencia de eventos que llevaron a la falla está documentada en el video Lake Oroville Spillway Incident Timeline. Para septiembre de 2018, el costo de las reparaciones y otros problemas derivados de la falla estructural de los vertederos ha sido estimado en $ 1.1 mil millones de dólares.
|
9.3 CURVA DE GASTO DEL VERTEDERO
|
|
La presión en la cresta del vertedero a la descarga de diseño está cerca de la presión atmosférica. La carga de diseño HD, la cual incluye la carga de velocidad, corresponde a la descarga de diseño. Las descargas menores que las de diseño producirán presiones en la cara del vertedero en exceso de la presión atmosférica, mientras que las descargas mayores producirán presiones en defecto (presiones subatmosféricas).
La descarga sobre un vertedero conopial abierto (sin compuertas) es (Roberson et al., 1998):
QD = CD (2 g)1/2 L HD 3/2 | (9-11) |
en la cual QD = descarga de diseño, CD = coeficiente adimensional, L = longitud de cresta, en la dirección perpendicular al flujo, y HD = carga de diseño total sobre la cresta, incluyendo la carga de velocidad inmediatamente aguas arriba ha.
La Figura 9-15 muestra los valores de CD en función de P/HD, en la cual P = altura de la cresta del vertedero medida desde el lecho del canal. Para valores grandes de P/HD, el valor de CD se acerca asintóticamente a un valor de CD = 0.492.
En general, la descarga sobre vertederos de tipo conopial es:
Q = C (2 g)1/2 L H 3/2 | (9-12) |
en la cual Q = descarga, C = coeficiente adimensional, L = longitud de la cresta, en dirección perpendicular al flujo, y H = carga sobre la cresta, incluyendo la carga de velocidad inmediatamente aguas arriba.
|
La variación de C/CD en función de H/HD se muestra en la Fig. 9-16. Las Figuras 9-15 y 9-16 pueden usarse para desarrollar la curva de gasto, es decir, una relación entre el gasto Q y la carga H. Si la carga actual H excede la carga de diseño HD, se desarrollarán presiones subatmosféricas en el vertedero, lo cual puede conducir a daños por cavitación. Para evitar estos daños, la carga de presión negativa debe ser menor de 20 pies.
|
|
Curva de gasto del vertedero: Ejemplo
Determinar la curva de gasto para un vertedero de tipo conopial con longitud L = 30 m. La carga de diseño es: HD = 10 m. El bordo libre es: Fb = 5 m. La elevación de la cresta del vertedero es 1,000 m. La elevación del lecho del río es 970 m. Suponer que la velocidad inmediatamente aguas es despreciable. Solución
Los cálculos se resumen en la Tabla 9-2.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ejemplo 9-1.
|
9.4 EL SALTO HIDRÁULICO
|
|
El salto hidráulico es un fenómeno de la hidráulica de canales en el cual el flujo cambia repentinamente de supercrítico a subcrítico (Fig. 9-18). La ecuación del salto hidráulico se desarrolla para un canal horizontal, para el cual el salto es estacionario, es decir, se presenta en un lugar específico del canal. Un salto hidráulico no estacionario puede ocurrir en un canal no horizontal. En la práctica, es preferible usar el salto hidráulico estacionario sobre el salto no estacionario (salto en movimiento).
|
El salto hidráulico se utiliza en las siguientes aplicaciones:
-
Para disipar la energía en el agua que fluye sobre presas, vertederos, y otras estructuras hidráulicas, evitando así la erosión de las estructuras localizadas aguas abajo.
-
Para recuperar la carga hidráulica aguas abajo de una sección de medición.
-
Para aumentar el peso en una solera, reduciendo así las presiones de levantamiento bajo una estructura de mampostería.
-
Para airear el agua con el propósito de purificación.
La ecuación del salto hidráulico
Un salto hidráulico se formará en un canal rectangular cuando se cumpla la siguiente ecuación (Ver Ejemplo 3-1):
y2 1 | (9-13) |
en la cual y1 = profundidad de flujo aguas arriba (supercrítico), y2 = profundidad de flujo aguas abajo (subcrítico), y F1 = el número de Froude aguas arriba. La profundidad y1 es la profundidad inicial y y2 es la profundidad secuente.
La ecuación del salto hidráulico (Ec. 9-13) se muestra en la Fig. 9-19.
Nótese que para el número de Froude
|
Ejemplo 9-2.
|
Tipos de salto hidráulico
Los saltos hidráulicos se clasifican como se muestra en la Tabla 9-3.
| Tabla 9-3 Tipos de salto hidráulico. | ||
| Número de Froude aguas arriba F1 | Tipo de salto | Descripción gráfica |
| 1.0 - 1.7 | Salto ondular |  |
| 1.7 - 2.5 | Salto débil | 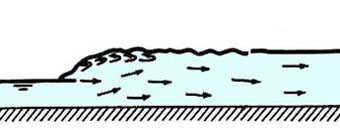 |
| 2.5 - 4.5 | Salto oscilante | 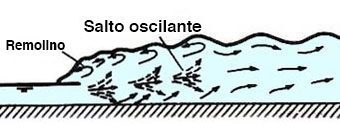 |
| 4.5 - 9.0 | Salto estable |  |
| > 9.0 | Salto fuerte | 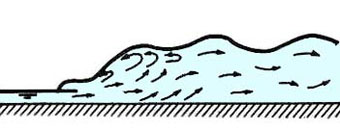 |
Características del salto hidráulico
La pérdida de energía es:
(y2 - y1)3 | (9-14) |
| [Véase también Video Laboratorio: El salto hidráulico]. |
La pérdida de energía relativa es:
ΔE E2 | (9-15) |
La eficiencia del salto es (véase el recuadro de abajo):
E2 ( 1 + 8 F12 )3/2 - 4 F12 + 1 | (9-16) |
La altura del salto es:
| (9-17) |
La altura relativa del salto es:
hj y2 y1 | (9-18) |
en la cual y1 /E1 = la profundidad inicial
relativa, y y2 /E1 = profundidad secuente
relativa.
En términos del número de Froude aguas arriba, la altura relativa del salto es:
hj ( 1 + 8 F12 )1/2 - 3 | (9-19) |
Una representación gráfica de las características del salto hidráulico se muestra en la Fig. 9-20. Puede observarse lo siguiente:
-
La profundidad secuente relativa alcanza un valor máximo y2 /E1 = 0.8 para F1 = 1.73.
-
La altura relativa del salto alcanza un valor máximo hj /E1 = 0.507 para F1 = 2.77.
-
Se confirma que para F1 = 1, la profundidad inicial y1 es igual a 2/3 (es decir, 0.667) de la energía específica E1.
Para F > 3, los cambios en todas las características se vuelven graduales.
|
|
Eficiencia
del salto hidráulico
Con referencia a la Fig. 9-21, la eficiencia del salto hidráulico es:
F1 = v1 / (gy1)1/2
F2 = v2 / (gy2)1/2
v1y1 = v2 y2
v12y12 = v22 y22
F12 y13 = F22 y23
F22 = F12 / (y2
/ y1)3
La ecuación del salto hidráulico es (Ec. 9-13):
y2 / y1 = (1/2) [ (1 + 8 F12)1/2 - 1 ]
N 2 = 1 + 8 F12
y2 / y1 = (1/2) [ N - 1]
2 (y2 / y1) = N - 1
(y2 / y1)3 = (1/8) [ N - 1]3
2 (y2 / y1)3 = (1/4) [ N - 1]3
N = ( 1 + 8 F12)1/2
N 3 = ( 1 + 8 F12)3/2
N 2 - 1 = 8 F12
F12 = ( N 2 - 1) / 8
4 F12 = ( N 2 - 1) / 2
La eficiencia
del salto hidráulico es:
E2/E1 = [ y2 + v22/(2g) ] / [ y1 + v12/(2g) ]
E2/E1 = [ y2(1 + F22/2) ] / [ y1(1 + F12/2) ]
E2/E1 = 2 (y2/y1) {1 + F12 / [ 2 (y2/y1)3] } / (2 + F12)
E2/E1 = (N - 1) {1 + (N 2 - 1) / [ 2 (N - 1)3 ] } / (2 + F12)
E2/E1 = (N 2 - 1)(N - 1) {1 + (N 2 - 1) / [ 2 (N - 1)3 ] } / [8 F12(2 + F12) ]
E2/E1 = [ (N 2 - 1)(N - 1) + (1/2)(N + 1)2 ] / [ 8 F12(2 + F12) ]
E2/E1 = { (N 3 - N 2 - N - 1) + [ (N 2/2) + N + (1/2)] } / [ 8 F12(2 + F12) ]
E2/E1 = { (N 3 - [(N 2 - 1)/2] + 1} / [ 8 F12 (2 + F12) ]
E2/E1 = [ (1 + 8 F12)3/2 - 4F12 + 1] / [ 8 F12(2 + F12) ] RESPUESTA.
|
Ejemplo 9-3.
|
Ejemplo 9-4.
|
Longitud del salto hidráulico
La longitud del salto hidráulico es la distancia medida
desde la cara frontal a un punto (en la superficie del agua) situado
inmediatamente aguas abajo del rodillo (ver recuadro de la Fig. 9-21).
La longitud relativa del salto L/y2 se determina experimentalmente, variando de 5.0 a 6.15 aproximadamente, para un rango amplio de
números de Froude aguas arriba. En el rango de
|
Las mediciones experimentales han mostrado que el perfil de la superficie
del salto hidráulico real varía con el
número de Froude aguas arriba.
Los perfiles adimensionales típicos
se muestran en la
|
|
PREGUNTAS
|
|
-
¿Cómo se diferencía el flujo rápidamente variado del gradualmente variado?
-
¿Existe una solución teórica para el flujo unidimensional rápidamente variado?
-
¿Cuál es el exponente de la curva de gasto para un vertedero de cresta ancha?
-
¿Cuál es el coeficiente de gasto para los vertederos de gran altura en unidades acostumbradas en EE.UU.?
-
¿Qué significa "conopial"?
-
¿Cuál es la justificación para el uso de un vertedero tipo laberinto?
-
¿Cuál es el riesgo cuando el flujo en un vertedero excede la descarga de diseño?
-
¿Qué condición de flujo resulta en un salto hidráulico?
-
La ecuación del salto hidráulico es lineal o no lineal?
-
¿Cómo se mide la longitud del salto hidráulico?
PROBLEMAS
|
|
-
Se proyecta un vertedero de emergencia para el Lago de Conservación Demerara para salvaguardar la integridad de la presa bajo condiciones de cambio climático (similar al de la
Fig. 9-24). Suponer que las compuertas de avenidas existentes serían inoperables durante una gran inundación debido al alto nivel aguas abajo. Determinar la longitud del vertedero requerida para pasar la Avenida Máxima Probable (AMP). Usar los siguientes datos:-
AMP de 1 día de duración: 428 mm
-
Abstracción hidrológica: 18 mm
-
Área de drenaje: 582 km2
-
Tiempo de base del hidrograma de avenida: 3 días
-
Elevación de la cresta del terraplén de la presa:
-
Elevación de la cresta del vertedero: 17.526 m
-
Bordo libre: 0.3 m
-
Coeficiente de descarga del vertedero de cresta ancha: 1.45
Para simplificar, suponer un hidrograma de avenidas de forma triangular. Utilizar todo el bordo libre para contener la AMP.

Fig. 9-24 El vertedero de 8000 pies del Lago de Conservación Boerasirie.
-
-
Diseñar una sección de vertedero WES con una cara vertical aguas arriba y una longitud de cresta
L = 150 pies. La descarga de diseño es Q = 50,000 pies3/s. El nivel aguas arriba a la descarga de diseño está en la Elev. 750 pies, y el fondo de canal está en la Elev. 650 pies (véase la Fig. 9-6 para el ejemplo gráfico). -
Usar CURVA DE GASTO CONOPIAL EN LÍNEA para calcular el gasto de un vertedero conopial de longitud
L = 15 m, carga de diseño Hd = 2 m, elevación de la cresta = 1045 m, elevación del lecho del río = 1000 m, y bordo libre Fb = 1 m. Despreciar la carga de velocidad inmediatamente aguas arriba. ¿Cuál debe ser la longitud del vertedero para pasar la Avenida Máxima ProbableQAMP = 250 m3/s usando todo el bordo libre? Expresar la longitud del vertedero a una precisión 0.1 m por exceso. -
Demostrar la Ec. 9-14.
-
Demostrar la Ec. 9-19.
-
Calcular la pérdida de energía en un salto hidráulico, dadas las profundidades secuentes
y1 = 0.58 m yy2 = 2.688 m. -
Calcular la altura relativa del salto hidráulico hj / E1 para F1 = 3.
-
Usar CANAL EN LÍNEA 11 para calcular la profundidad secuente y2 a través de un salto hidráulico, dadas la descarga q = 5 m2/s y la profundidad inicial y1 = 0.58 m.
-
Usar CANAL EN LÍNEA 12 para determinar la profundidad secuente y2 y la pérdida de energía ΔE a través de un salto hidráulico, dadas la descarga q = 10 pies2/s y la profundidad inicial y1 = 0.5 pies.
-
Usar CANAL EN LÍNEA 16 para calcular las profundidades secuentes a través de un salto hidráulico, dadas la descarga q = 10 pies2/s y la pérdida de energía ΔE = 3.287 pies.
-
Usar CANAL EN LÍNEA 16 para calcular las profundidades secuentes a través de un salto hidráulico, dadas la descarga q = 5 m2/s y la pérdida de energía ΔE = 1.5 m.
-
Usar CANAL EN LÍNEA 18 para calcular la eficiencia del salto hidráulico E2/E1 para
q = 10 pies2/s y y1 = 0.5 pies.
BIBLIOGRAFÍA
|
|
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York.
Roberson, J. A., J. J. Cassidy, y M. H. Chaudhry. 1998. Hydraulic Engineering. John Wiley and Sons, New York, Second edition.
Pugh, C. A., y E. W. Gray. 1984. Fuse Plug Embankments in Auxiliary Spillways - Developing Design Guidelines and Parameters, United States Committee on Large Dams (citado por el U.S. Bureau of Reclamation en su sitio web).
| http://hidraulicadecanales.sdsu.edu |
|
181108 15:30 |




























