|
Flood stage on the Chané river, Santa Cruz department, Bolivia (January 1990). THE COURANT NUMBER
Professor Emeritus of Civil and Environmental Engineering
San Diego State University, San Diego,
California
1. INTRODUCTION
The Courant number
is a fundamental concept in the field of Computational Fluid Dynamics (CFD)
and, by extension, in Computational Hydraulics. The number effectively connects the physical and numerical properties
of a computational scheme, with specific
application to the convection problem, in other words,
the well-known advection of fluid mechanics. The Courant number is defined as the ratio of a physical velocity u
to the grid velocity Δx /Δt. In practice, the Courant number
is commonly expressed in the following form:
The name Courant recognizes the life work of Richard Courant, a renowned German-American mathematician
and early
contributor to the field of applied mathematics.
In this article, we endeavor to perform a contemporary analysis of the Courant number, throwing renewed
light onto its behavior. We focus specifically on the numerical
solution of the convection problem,
unveiling properties that may have been hitherto hidden in conventional
applications of computational fluid dynamics and hydraulics.
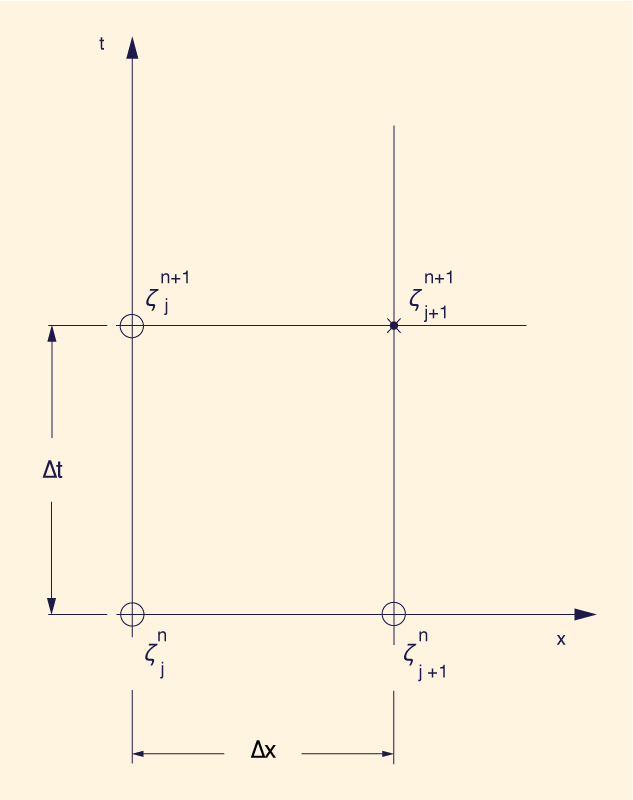
2. THE CONVECTION PROBLEM AND THE FOUR-POINT GENERAL SCHEME
In order to set the stage for the analysis
that will follow, we begin by conceptualizing the convection problem of fluid mechanics.
A physical quantity ζ will move,
in space x and time t,
with a certain convective velocity u following a first-order partial differential equation of the
following form (Ponce et al., 1979):
This equation may be
solved numerically in various ways.
A conveniently general explicit linear
In Equation 2, solving for the unknown value ζ j+1 n+1 leads to the following routing equation:
The routing coefficients are defined as follows:
in which C is the Courant number defined as follows:
For a given Courant number, with the weighting factors X and Y having been established beforehand, and using Eqs. 2 to 7, the computation proceeds to calculate the values of ζ for each and every one of the specified grid points in the computational domain.
Equation 3, with its supporting equations 4-7, constitutes a family of numerical schemes of the convection equation, Eq. 1.
Their stability and convergence properties depend on the values of
X, Y, and C.
The first two, referred to as weighting factors,
and C, the Courant number, uniquely characterize the chosen scheme. Ostensibly, the Courant number is
the ratio of the convective velocity u to the grid ratio or "grid velocity"
3. NUMERICAL DIFFUSION AND DISPERSION
Equation 1 describes convection, a first-order process; therefore,
diffusivity, a second-order process, and dispersivity, a third-order process,
are not accounted for (Ponce, 2023).
However, Eq. 2, a numerical solution of Eq. 1 will typically show a
diffusive and/or a dispersive behavior due to the finite grid size.
This is
attributed to numerical diffusion (the error of the first-order term of the scheme)
and numerical dispersion (the error of the second-order term).
A measure of the amount of numerical diffusion and dispersion
may be obtained from the approximation error of the finite difference scheme, Eq. 2.
This error may be obtained by expanding the grid function ζ(jΔx, nΔt) in Taylor series about point (jΔx, nΔt), leading to
(Cunge, 1969;
Ponce et al., 1979):
in which R = the approximation error. From Eq. 8, we note that for X = Y = 1/2, the scheme is of second-order accuracy. i.e., R = ο(Δx2). Furthermore, for C = 1,
the accuracy is of third order; that is, the numerical dispersion vanishes.
In point of fact, for X = Y = 1/2 and C = 1, the exact
solution of the convection equation (Eq. 1) is obtained.
In Equation 8, the coefficient of the second-order term ∂2ζ /∂x2
is referred to as the numerical diffusion coefficient and defined as follows:
Positive values of μn cause the scheme
to diffuse numerically;
negative values to amplify numerically.
While in the former convergence is impaired, in the latter stability suffers.
Both stability and convergence improve as
I. Forward-in-time, backward-in-space scheme features.
II. Forward-in-space, backward-in-time scheme features.
III. Backward-in-space, backward-in-time scheme features.
The present analysis enables the following conclusions:
Contrary to explicit schemes, implicit schemes have been favored in the past due to their perceived improved stability properties, purportedly featuring what has often been referred to as "unconditional stability". Experience, however, points otherwise. In a general sense, both explicit and implicit numerical schemes are subject to issues of stability and convergence. An appropriate von Neumann analysis is recommended to substantially improve numerical modeling practice (Ponce et al., 1978).
4. SUMMARY
In this paper
we focus on the role
of the Courant number in computational hydraulics, particularly
in the modeling of the pure convection problem.
We
throw a renewed light onto the properties of stability and convergence
of a class of popular explicit linear numerical schemes of the pure convection
equation.
REFERENCES
Courant, R., K. Friedrichs, and H. Lewy. 1928.
Über die partiellen Differenzengleichungen der mathematischen Physik,
Mathematische Annalen, vol. 100, p. 32-74.
Cunge, J. A. 1969.
On the Subject of a Flood Propagation Computation Method (Muskingum Method).
Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Ponce, V. M., H. Indlekofer, and D. B. Simons. 1978.
Convergence of four-point implicit water wave models.
Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY7,
July, 947-958.
Ponce, V. M., Y. H. Chen, and D. B. Simons. 1979.
Unconditional stability in convection computations. Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY9,
September, 1079-1086.
Ponce, V. M. 2014.
Engineering Hydrology: Principles and Practices. Second edition, online.
Ponce, V. M. 2023.
Is dispersion important in flood routing? Online paper.
Ponce, V. M. 2023.
When is the diffusion wave applicable? Online paper.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 231214 |