Río Alto Paraguay en Porto Murtinho, Mato Grosso do Sul, Brasil, el cual presenta un hidrograma de inundación de un año de duración, el máximo posible, claramente la ola de inundación por excelencia.


¿CUÁNDO ES LA ONDA DIFUSIVA APLICABLE?


Víctor M. Ponce

Profesor Emérito de Ingeniería Civil y Ambiental

Universidad Estatal de San Diego, California


23 septiembre 2025

RESUMEN.  Se ha realizado una revisión de las ondas difusivas y su uso en el enrutamiento de ondas de inundación. Las ondas difusivas se propagan con la celeridad de Seddon, es decir, la celeridad de la onda cinemática, y están sujetas a atenuación (difusión) relativamente pequeña. Estas propiedades coinciden claramente con las de las ondas de inundación típicas. Otras ondas de flujo en superficie libre, a saber, las cinemáticas, mixtas y dinámicas, ya sea (a) no son difusivas (ondas cinemáticas y dinámicas), o (b) son demasiado difusivas (ondas mixtas). En particular, se ha confirmado que las ondas mixtas son tan difusivas que ponen en duda su mera existencia. Los criterios de aplicabilidad de las ondas cinemáticas y difusivas muestran que estas últimas, las ondas difusivas, tienen un rango de aplicabilidad más amplio que el de las ondas cinemáticas. Por lo tanto, la onda difusiva es recomendada para aplicaciones prácticas de enrutamiento en la hidrología de inundaciones.

1.  INTRODUCCIÓN

The diffusion wave is a type of wave used in flood routing. Other types of waves are the kinematic wave and the mixed kinematic-diffusion wave, hereafter called "mixed wave" (Lighthill and Whitham, 1955; Ponce and Simons, 1977). Note that the mixed wave has been widely referred to in the literature as "dynamic wave", although this usage appears to be ill-advised, because it leads to a semantic confusion with the long-established dynamic wave of Lagrange (1788), a concept quite different from the mixed wave.

La onda de difusión es un tipo de onda utilizada en el encaminamiento de inundaciones. Otros tipos de ondas son la onda cinemática y la onda mixta cinemático-difusión, en adelante denominada "onda mixta" (Lighthill y Whitham, 1955; Ponce y Simons, 1977). Tenga en cuenta que la onda mixta ha sido ampliamente denominada en la literatura "onda dinámica", aunque este uso parece poco aconsejable, porque conduce a una confusión semántica con la onda dinámica establecida desde hace mucho tiempo por Lagrange (1788), un concepto bastante diferente de la onda mixta.

A comprehensive classification of shallow-water waves in open-channel flow was accomplished by Ponce and Simons (1977), who used linear stability theory to derive the celerity and attenuation functions of all four types of shallow-water waves: (1) kinematic waves, (2) diffusion waves, (3) mixed waves, and (4) dynamic waves. These wave types are defined in terms of the dimensionless wavenumber σ*, as shown in Fig. 1 (Ponce, 2023). Kinematic waves correspond to the smallest values of σ* (to the left of the scale), and dynamic waves to the largest (to the right of the scale). Mixed waves lie along the middle-to-right of the scale, while diffusion waves lie along the left-of-middle.

Ponce y Simons (1977) lograron una clasificación integral de las ondas de aguas poco profundas en el flujo de canales abiertos, quienes utilizaron la teoría de la estabilidad lineal para derivar las funciones de celeridad y atenuación de los cuatro tipos de ondas de aguas poco profundas: (1) ondas cinemáticas, (2) ondas de difusión, (3) ondas mixtas y (4) ondas dinámicas. Estos tipos de ondas se definen en términos del número de onda adimensional ~*, como se muestra en la Fig. 1 (Ponce, 2023). Las ondas cinemáticas corresponden a los valores más pequeños de ~* (a la izquierda de la escala) y las ondas dinámicas a los más grandes (a la derecha de la escala). Las ondas mixtas se encuentran en el centro a la derecha de la escala, mientras que las ondas de difusión se encuentran en el centro a la izquierda.

Ponce and Simons (1977)

Fig. 1   Dimensionless relative wave celerity cr* vs dimensionless wavenumber σ*.

In Figure 1, kinematic waves lie along the first log cycle (to the left), while dynamic waves lie along the fifth and sixth cycles (to the right), depending on the Froude number. Mixed waves lie mostly along the fourth and fifth cycles, while diffusion waves lie along the second and third cycles.

En la Figura 1, las ondas cinemáticas se encuentran a lo largo del primer ciclo logarítmico (a la izquierda), mientras que las ondas dinámicas se encuentran a lo largo del quinto y sexto ciclo (a la derecha), dependiendo del número de Froude. Las ondas mixtas se encuentran principalmente a lo largo del cuarto y quinto ciclo, mientras que las ondas de difusión se encuentran a lo largo del segundo y tercer ciclo.

Hydrodynamic theory asserts that if the wave celerity is a constant along the dimensionless wavenumber, wave attenuation is zero. In Figure 1, this condition corresponds to both kinematic waves (left of scale) and dynamic waves (right of scale). Conversely, if the wave celerity varies along the dimensionless wavenumber, as in the case of a mixed wave, wave attenuation is nonzero. Wave attenuation reaches a maximum at the point of zero curvature of the dimensionless relative celerity function cr* vs dimensionless wavenumber σ* (Fig. 1), i.e., when the second derivative is equal to zero. Experience indicates that these maximum values of wave attenuation may actually render the wave in question nonexistent, due to the extremely high rates of attenuation (Lighthill and Whitham, 1955).

La teoría hidrodinámica afirma que si la celeridad de la onda es constante a lo largo del número de onda adimensional, la atenuación de la onda es cero. En la Figura 1, esta condición corresponde tanto a ondas cinemáticas (a la izquierda de la escala) como a ondas dinámicas (a la derecha de la escala). Por el contrario, si la celeridad de la onda varía a lo largo del número de onda adimensional, como en el caso de una onda mixta, la atenuación de la onda es distinta de cero. La atenuación de la onda alcanza un máximo en el punto de curvatura cero de la función de celeridad relativa adimensional cr* frente al número de onda adimensional ~* (Fig. 1), es decir, cuando la segunda derivada es igual a cero. La experiencia indica que estos valores máximos de atenuación de la onda pueden en realidad hacer que la onda en cuestión no exista, debido a las tasas de atenuación extremadamente altas (Lighthill y Whitham, 1955).

Thus, the question remains: If the kinematic waves have no attenuation, and the mixed waves are subject to very strong attenuation, what happens to the diffusion waves, which ostensibly lie in between them? The answer is: The diffusion waves are subject to a small but finite amount of attenuation, which is generally much smaller than the strong attenuation featured by mixed waves.

Por lo tanto, la pregunta sigue siendo: si las ondas cinemáticas no tienen atenuación y las ondas mixtas están sujetas a una atenuación muy fuerte, ¿qué sucede con las ondas de difusión, que aparentemente se encuentran entre ellas? La respuesta es: las ondas de difusión están sujetas a una cantidad pequeña pero finita de atenuación, que generalmente es mucho menor que la fuerte atenuación que presentan las ondas mixtas.

In this article, we make the case for the diffusion wave. We note that if the flood wave has a small amount of attenuation, the diffusion wave model will account for it, while the kinematic wave model will not. Furthermore, we show that due to the large amounts of attenuation which are predicted for mixed waves, the latter are not very likely to occur in the real world. In Section 2, we explain the nature of flood waves and make a point of the need to focus on the diffusion wave. With the applicability question clearly answered in Section 4, the time has come to hail the diffusion wave as the method of choice in flood routing engineering practice.

En este artículo, defendemos la onda de difusión. Observamos que si la onda de inundación tiene una pequeña cantidad de atenuación, el modelo de onda de difusión la tendrá en cuenta, mientras que el modelo de onda cinemática no. Además, mostramos que debido a las grandes cantidades de atenuación que se predicen para las ondas mixtas, es poco probable que estas últimas ocurran en el mundo real. En la Sección 2, explicamos la naturaleza de las ondas de inundación y destacamos la necesidad de centrarnos en la onda de difusión. Con la respuesta clara a la pregunta de aplicabilidad en la Sección 4, ha llegado el momento de aclamar la onda de difusión como el método de elección en la práctica de ingeniería de encaminamiento de inundaciones.

2.  NATURALEZA DE UNA ONDA DE INUNDACIÓN

What is the nature of a flood wave? Essentially, a flood wave is a "long" wave, i.e., one of small dimensionless wavenumber (Fig. 1), traveling at, or very close to, the kinematic wave celerity, and experiencing little attenuation. Seddon (1900) pioneered the study of flood waves, concluding that its celerity could be expressed as the slope of the discharge-area rating Q = αAβ, in which Q = discharge, A = flow area, and α and β are coefficient and exponent, respectively.

¿Cuál es la naturaleza de una ola de inundación? Esencialmente, una onda de inundación es una onda "larga", es decir, una con un número de onda pequeño y adimensional (Fig. 1), que viaja a la velocidad de la onda cinemática o muy cerca de ella y experimenta poca atenuación. Seddon (1900) fue pionero en el estudio de las ondas de inundación y concluyó que su celeridad podría expresarse como la pendiente de la clasificación del área de descarga Q = ~A~, en la que Q = descarga, A = área de flujo, y ~ y ~ son coeficiente y exponente, respectivamente.

Según Seddon, la celeridad de una onda de inundación es: c = dQ/dA, en la que dA = (1/T)dy, con T = ancho superior del canal (corriente), e y = nivel o elevación de la superficie del agua. Expresó la celeridad de una onda de inundación como c = (1/T) dQ/dy. Por tanto, una onda de inundación es esencialmente una onda cinemática sujeta a una cantidad relativamente pequeña de difusión. De hecho, ésta es la onda cinemática con difusión de Lighthill y Whitham (1955) o, más concisamente, la onda de difusión de Ponce y Simons (1977).

According to Seddon, the celerity of a flood wave is: c = dQ/dA, in which dA = (1/T)dy, with T = (stream) channel top width, and y = stage, or water surface elevation. He expressed the celerity of a flood wave as c = (1/T) dQ/dy. Thus, a flood wave is essentially a kinematic wave subject to a relatively small amount of diffusion. Indeed, this is the kinematic-wave-with-diffusion of Lighthill and Whitham (1955) or, more concisely, the diffusion wave of Ponce and Simons (1977).

Según Seddon, la celeridad de una onda de inundación es: c = dQ/dA, en la que dA = (1/T)dy, con T = ancho superior del canal (corriente), e y = nivel o elevación de la superficie del agua. Expresó la celeridad de una onda de inundación como c = (1/T) dQ/dy. Por tanto, una onda de inundación es esencialmente una onda cinemática sujeta a una cantidad relativamente pequeña de difusión. De hecho, ésta es la onda cinemática con difusión de Lighthill y Whitham (1955) o, más concisamente, la onda de difusión de Ponce y Simons (1977).

As long as diffusion needs to be accounted for, diffusion waves may not be modeled with kinematic waves, because the latter feature zero diffusion. We note that in the 1980s, kinematic waves were solved using numerical models, and the latter did feature some diffusion. This diffusion, however, was uncontrolled numerical diffusion, and not related to the true physical diffusion of the flood wave; therefore, the results of the routing varied with the choice of grid size.

Siempre que sea necesario tener en cuenta la difusión, las ondas de difusión no pueden modelarse con ondas cinemáticas, porque estas últimas presentan difusión cero. Observamos que en la década de 1980 las ondas cinemáticas se resolvían mediante modelos numéricos, y estos últimos presentaban cierta difusión. Esta difusión, sin embargo, fue una difusión numérica incontrolada y no estuvo relacionada con la verdadera difusión física de la onda de inundación; por lo tanto, los resultados del enrutamiento variaron según la elección del tamaño de la cuadrícula.

Could the flood wave be construed as a mixed wave, a wave that sits on the middle-to-right of the dimensionless wavenumber spectrum (Fig. 1)? The answer is: Not likely for typical flood waves, which hold their stage and do not attenuate very much. If the flood wave were to attenuate strongly, it would cease to be a flood wave, instead joining the mass of the underlying equilibrium, steady flow. Thus, we conclude that mixed waves are not an appropriate model of flood waves, at least, not in the general case. In the following section, calculations of diffusion waves will confirm these statements.

¿Podría interpretarse la onda de inundación como una onda mixta, una onda que se sitúa en el centro a la derecha del espectro de números de onda adimensionales (Fig. 1)? La respuesta es: no es probable que se trate de ondas de inundación típicas, que mantienen su fase y no se atenúan mucho. Si la onda de inundación se atenuara fuertemente, dejaría de ser una onda de inundación y se uniría a la masa del equilibrio subyacente, el flujo constante. Por tanto, concluimos que las ondas mixtas no son un modelo apropiado de ondas de inundación, al menos no en el caso general. En la siguiente sección, los cálculos de las ondas de difusión confirmarán estas afirmaciones.

Having placed aside: (a) the kinematic waves, because they lack diffusion entirely, and (b) the mixed waves, because they have too much diffusion, we are left only with the diffusion wave, which lies in between kinematic and mixed waves in the dimensionless wavenumber spectrum. This is the wave that truly embodies the nature of flood waves: A kinematic wave featuring a small, but perceptible, amount of diffusion.

Habiendo dejado de lado: (a) las ondas cinemáticas, porque carecen por completo de difusión, y (b) las ondas mixtas, porque tienen demasiada difusión, nos queda solo la onda de difusión, que se encuentra entre las ondas cinemáticas y mixtas en el espectro de números de onda adimensional. Esta es la onda que realmente encarna la naturaleza de las ondas de inundación: una onda cinemática que presenta una cantidad de difusión pequeña, pero perceptible.

3.  LA ONDA DIFUSIVA

According to theory, the dimensionless relative celerity of a diffusion wave resembles that of a kinematic wave, but unlike the latter, it increases, ever so slightly with the dimensionless wavenumber σ* (Fig. 1). This increase is the source of the wave diffusion which characterizes the diffusion wave.

Según la teoría, la celeridad relativa adimensional de una onda de difusión se parece a la de una onda cinemática, pero a diferencia de esta última, aumenta, muy ligeramente, con el número de onda adimensional ~* (Fig. 1). Este aumento es la fuente de la difusión de ondas que caracteriza a la onda de difusión.

Ponce and Simons (1977)

Fig. 1   Dimensionless relative wave celerity cr* vs dimensionless wavenumber σ*.

The amount of wave diffusion is expressed in terms of the logarithmic decrement δ, a measure of the rate at which the wave changes upon propagation (Wylie, 1966). The definition of logarithmic decrement is: δ = ln Q1 - ln Q0, or, alternatively: Q1 = Q0 eδ, in which Q0 = flood discharge at the start of the measurement, and Q1 = flood discharge after an elapsed time equal to one (sinusoidal) period of propagation.

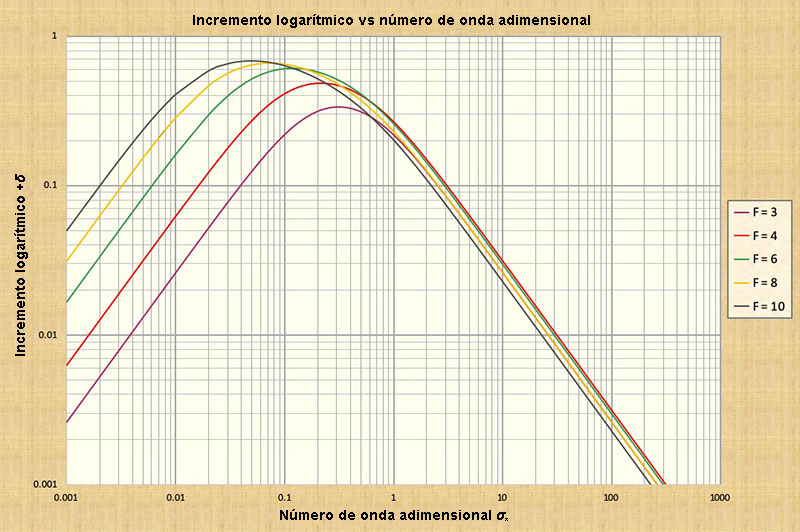
La cantidad de difusión de la onda se expresa en términos del decremento logarítmico ~, una medida de la velocidad a la que la onda cambia durante la propagación (Wylie, 1966). La definición de decremento logarítmico es: ~ = ln Q1 - ln Q0, o, alternativamente: Q1 = Q0 e~, en la que Q0 = caudal de inundación al inicio de la medición, y Q1 = caudal de inundación después de un tiempo transcurrido igual a un período de propagación (sinusoidal).

The discharge decreases for a negative value of δ, causing wave attenuation, corresponding to Froude number F < 2 (Vedernikov number V < 1); it increases for a positive value, a logarithmic increment, causing wave amplification, corresponding to Froude number F > 2 (V > 1) (Ponce, 1991).

La descarga disminuye para un valor negativo de ~, provocando atenuación de la onda, correspondiente al número de Froude F < 2 (número de Vedernikov V < 1); aumenta para un valor positivo, un incremento logarítmico, provocando una amplificación de la onda, correspondiente al número de Froude F > 2 (V > 1) (Ponce, 1991).

Ponce and Simons (1977) have used linear stability theory to calculate the logarithmic decrement of the diffusion wave. The expression is: δd = (2 π /3) σ*. Note that in this expression, as σ* → 0, the logarithmic decrement δd → 0, confirming that a kinematic wave is not subject to attenuation. Moreover, note that for σ* → ∞, the diffusion wave logarithmic decrement δd → ∞, confirming the inability of the diffusion wave logarithmic decrement formula to account for the dynamic waves, which also feature zero attenuation.

Ponce y Simons (1977) han utilizado la teoría de la estabilidad lineal para calcular el decremento logarítmico de la onda de difusión. La expresión es: ~d = (2 ~ /3) ~*. Tenga en cuenta que en esta expresión, cuando ~* ~ 0, el decremento logarítmico ~d ~ 0, confirma que una onda cinemática no está sujeta a atenuación. Además, tenga en cuenta que para ~* ~ ~, el decremento logarítmico de la onda de difusión ~d ~ ~, lo que confirma la incapacidad de la fórmula de decremento logarítmico de la onda de difusión para tener en cuenta las ondas dinámicas, que también presentan atenuación cero.

Figure 2 shows the variation of the logarithmic decrement for all wave types, through the range of dimensionless wavenumbers from 0.001 to 1000, for Froude numbers F < 2. Moreover, Figure 3 shows the variation of the logarithmic increment for all wave types, through the range of dimensionless wavenumbers from 0.001 to 1000, for Froude numbers F > 2.

La Figura 2 muestra la variación del decremento logarítmico para todos los tipos de onda, a través del rango de números de onda adimensionales de 0,001 a 1000, para números de Froude F < 2. Además, la Figura 3 muestra la variación del incremento logarítmico para todos los tipos de onda, a través del rango de números de onda adimensionales de 0,001 a 1000, para números de Froude F > 2.

Ponce and Simons (1977)

Fig. 2   Logarithmic decrement -δ  vs dimensionless wavenumber σ* for Froude F < 2.

Ponce and Simons (1977)

Fig. 3   Logarithmic increment +δ  vs dimensionless wavenumber σ* for Froude F > 2.

Table 1 shows values of the diffusion wave logarithmic decrement δd  relevant in the present context. The examination of this table leads to the conclusions summarized in Box A.

La Tabla 1 muestra los valores del decremento logarítmico de la onda de difusión ~d relevantes en el contexto actual. El examen de este cuadro conduce a las conclusiones resumidas en el Cuadro A.

Table 1. Logarithmic decrement of the diffusion wave across the dimensionless wavenumber spectrum.
[1][2][3] [4][5] [6]
No. Dimensionless wavenumber σ* Logarithmic decrement δdeδdWave attenuation
(1 - eδd)		Wave type
00.00010.00020944 10Kinematic
10.0010.00209440.9980.002Kinematic/diffusion
20.010.0209440.9790.021Diffusion
30.10.209440.8110.189Diffusion
3a0.170.356040.7000.300Diffusion/Mixed
412.09440.1230.877Mixed
510.20.94401Mixed
6100.N.A.N.A.N.A.Dynamic 1
71000.N.A.N.A.N.A.Dynamic 1

1 In Col. 6, lines 6 and 7 are labeled as "Dynamic". The diffusion wave logarithmic decrement δd does not apply after the peak of attenuation is reached, i.e., in the dynamic wave range (see Fig. 2)./En la Col. 6, las líneas 6 y 7 están etiquetadas como "Dinámicas". El decremento logarítmico de la onda de difusión ~d no se aplica después de alcanzar el pico de atenuación, es decir, en el rango de onda dinámico (ver Fig. 2).

Box A.  Conclusions from Table 1./Cuadro A. Conclusiones de la Tabla 1.

  1. For very small dimensionless wavenumbers (see Line 0), the wave attenuation, shown in Col. 5, is zero, i.e., a kinematic wave.

  2. Para números de onda adimensionales muy pequeños (ver Línea 0), la atenuación de la onda, que se muestra en la Col. 5, es cero, es decir, una onda cinemática.

  3. For small dimensionless wavenumbers (see Line 2), the wave attenuation, shown in Col. 5, is 0.021 (2.1%) , i.e., a diffusion wave.

  4. Wave attenuation reaches 0.3, a high number (30%) for σ* = 0.17; i.e., at the limit between diffusion and mixed waves.

  5. Wave attenuation reaches 0.877, a very high number (87.7%), for σ* = 1 , i.e., a mixed wave.

  6. Wave attenuation reaches 1, the maximum value (100%), for σ* = 10, i.e., a mixed wave.

We confirm that kinematic waves are not subject to attenuation. We also confirm that for the midrange value of dimensionless wavenumber σ* > 0.17, the wave attenuation is greater than 30%, a threshold which is widely considered to be the division between diffusion waves (of limited wave diffusion, less than 30%) and mixed waves (of unlimited wave diffusion, which could readily reach 100%) (Flood Studies Report, 1975). Thus, the rationale for the argument that mixed waves are very strongly dissipative and, in most cases of practical interest, that they will not likely be there for us to calculate them (Ponce, 1992).

We confirm the following observations, based on detailed calculations, in reference to Fig. 1: (a) kinematic waves lie along the first log cycle; (b) diffusion waves along the second and third, (c) mixed waves along the fourth and fifth, and (d) dynamic waves along the fifth and sixth cycles, the latter depending heavily on the Froude number. Kinematic waves do not attenuate, mixed waves attenuate very strongly, and dynamic waves, being characteristically short, do not resemble flood waves, which are demonstrably long. Thus, a strong case is made for the applicability of the diffusion wave for flood routing applications.

4.  APLICABILIDAD DE LAS ONDAS DIFUSIVAS

Having shown that diffusion waves are applicable to the flood routing problem, we now show just how applicable they are. Here we elaborate on the work of Ponce and others (1978), who established the criterion for the applicability of kinematic and diffusion waves in terms of flood wave properties.

For the kinematic wave model, Ponce and others stated that to achieve at least 95% accuracy of the kinematic wave solution after one period of propagation, the dimensionless period has to satisfy the following inequality: τ* ≥ 171. The dimensionless period is defined as follows: τ* = T So (uo /do), in which T = period of the perturbation, So = channel (stream) bottom slope, uo = mean equilibrium flow velocity, and do = equilibrium flow depth. For example, given the following data: uo = 3 fps, do = 10 ft, and So = 0.0001, the resulting wave period is: T > (171 × 10) / ( (0.0001 × 3) = 5,700,000 seconds = 65.97 days. In other words, the duration of the flood must be greater than about 66 days for the kinematic wave solution to be at least 95% accurate after one period or propagation. It follows that the longer the flood duration, the more kinematic the flood wave is, and this finding agrees admirably with the theory.

For the diffusion wave model, Ponce and others compared the logarithmic decrement of the diffusion wave δd with that of the full solution (Fig. 2), and concluded that to achieve at least 95% accuracy of the diffusion wave solution after one period of propagation, the dimensionless period has to satisfy the following inequality: τ* ≥ 30. In this case, the dimensionless period is defined as follows: τ* = T So (g /do)1/2, in which g = gravitational acceleration. Using the previous example for comparison, for do = 10 ft, and So = 0.0001, the resulting wave period is: T > 30 / ( (0.0001 × [32.17/10)1/2] = 167,261 seconds = 1.93 days. In other words, the duration of the flood wave must be greater than 1.93 days (about 2 days) for the diffusion wave solution to be at least 95% accurate after one period or propagation. This finding reveals that the theory of diffusion waves is correct: These waves will apply for a larger number of cases than the kinematic wave. For the example presented here, a flood wave would need to have a minimum duration of 66 days for the kinematic wave to apply; however, for the diffusion wave, a minimum of only 2 days will suffice. Thus, we confirm the broad range of practical cases for which the diffusion wave is applicable.

5.  UN EJEMPLO PRÁCTICO

The concepts elaborated in the previous section are applied here to the Upper Paraguay river, in Mato Grosso do Sul, Brazil, and neighboring Bolivia. This river features a unique geographical setting, flowing through a continental delta encompassing the Pantanal of Mato Grosso, the largest wetland in the world, spanning 136,700 km2. The geomorphological and hydrological setting of the Upper Paraguay river has been described by Ponce (1995).

Fig. 4  Upper Paraguay river near Ladario, Mato Grosso do Sul, Brazil.

The flood hydrograph of the Upper Paraguay river, in its lower reaches, from Ladario to Porto Murtinho, comprising a distance of 520 km along the river, features only one peak flow stage, a condition attributed to the extreme runoff diffusion caused by the very small slope of the river channel, which varies between 2.34 cm/km near Ladario, and 0.83 cm/km near Porto Murtinho, for an average of 1.6 cm/km.

Downstream of Ladario, the river stage rises from March to August, receding from September to February. The peak stage occurs typically in the month of June and the low stages in December. The mean flow depth varies between 5.24 m at Ladario and 12.28 m at Porto Murtinho, for an average of 8.76 m. Moreover, the mean speed of propagation of the flood wave has been estimated at 0.1 m/s (Ponce, 1995). Thus, the values relevant to the assessment of flood wave model applicability are the following: T = 12 months, So = 0.000016, uo = 0.1 m/s, and do = 8.76 m. The calculations are summarized in Box B.

Fig. 5  Upper Paraguay river near Porto Murtinho, Mato Grosso do Sul, Brazil.

Box B.  Summary of calculations of flood wave model applicability.

  1. Relevant data: T = 12 months, So = 0.000016, uo = 0.1 m/s, and do = 8.76 m.

  2. Kinematic wave applicability relation: τ* = T So (uo /do) ≥ 171

  3. τ* = 12 mo × 30 days/mo × 86,400 sec/day × 0.000016 × 0.1 m/sec / 8.76 m = 5.68

  4. τ* = 5.68 << 171. Therefore, the kinematic wave model is not applicable.
    This is attributed to the very mild channel slope (1.6 cm/km).

  5. Diffusion wave applicability relation: τ* = T So (g /do)1/2 ≥ 30.

  6. τ* = 12 mo × 30 days/mo × 86,400 sec/day × 0.000016 × (9.81 m/sec2 / 8.76 m)1/2 = 527

  7. τ* = 527 >> 30. Therefore, the diffusion wave model is applicable.
    Even with this very small channel slope (1.6 cm/km), the diffusion wave model remains applicable.

6.  CONCLUSIONES

A review of diffusion waves and their use for routing flood waves has been accomplished. Diffusion waves travel with the Seddon celerity, i.e., the kinematic wave celerity, and are subject to little attenuation (diffusion). These properties distinctly match those of typical flood waves. Other free-surface flow waves, namely, kinematic, mixed, and dynamic, are either nondiffusive (kinematic and dynamic), or too diffusive (mixed). In particular, the mixed waves are confirmed to be so greatly diffusive as to question their mere existence altogether. Criteria for the applicability of both kinematic and diffusion waves show that the latter, the diffusion waves, have a broader range of applicability than do the kinematic waves. Therefore, the diffusion wave is recommended for practical applications in flood hydrology. An application to field data from the Upper Paraguay river, in Mato Grosso do Sul, Brazil, further confirms the findings of this study.

REFERENCIAS

Lagrange, J. L. de. 1788. Mécanique Analytique, Paris, part 2, section II, article 2, 192.

Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol.XLIII, 179-243, June.

Lighthill, M. J. and G. B. Whitham. 1955. On kinematic waves. I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

Wylie, C. R. 1966. Advanced Engineering Mathematics, 3rd ed., McGraw-Hill Book Co., New York, NY.

Flood Studies Report. 1975. Vol. III: Flood Routing Studies, Natural Environment Research Council, London, England.

Ponce, V. M. and D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of the Hydraulics Division, ASCE, 103(12), 1461-1476.

Ponce, V. M., R. M. Li, and D. B. Simons. 1978. Applicability of kinematic and diffusion models. Journal of the Hydraulics Division, ASCE, 104(3), 353-360.

Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M. 1992. Kinematic wave modeling: Where do we go from here? International Symposium on Hydrology of Mountainous Areas, Shimla, India, May 28-30.

Ponce, V. M. 1995. Hydrologic and environmental impact of the Parana-Paraguay waterway on the Pantanal of Mato Grosso, Brazil. https://ponce.sdsu.edu/hydrologic_and_environmental_impact_of_the_parana_paraguay_waterway.html

Ponce, V. M. 2023. Kinematic and dynamic waves: The definitive statement. Online article.

250922 1600