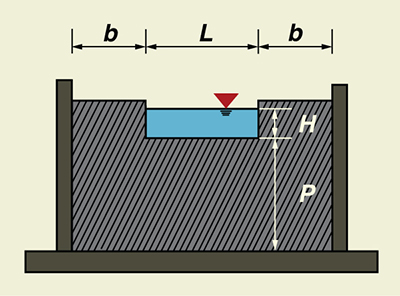
|
Online Standard Contracted Rectangular Weir Calculator
131108
The program online_standard_contracted_rectangular
calculates the
discharge through a standard contracted rectangular weir.
To be fully contracted, the overflow plate sides and ends must be located
at a distance of at least 2H
from the approach flow boundaries. The head is measured at a distance upstream
of at least 4H from the weir.
The computation procedure follows Section 9 of Chapter 7 of
the USBR Water Measurement Manual.
Fig. 1 Definition sketch for a standard contracted rectangular weir. The formula for the standard contracted rectangular weir is the Francis equation. In U.S. Customary units, this equation is:
in which Q = discharge, in cfs, L = length of the weir crest, in ft, and H = head on the weir crest, in ft.
The accuracy of measurements obtained by Eq. 1
is considerably less than that obtainable with V-notch weirs. The accuracy of the discharge coefficient is Equation 1 has a constant discharge coefficient (3.33), which facilitates computations. However, the coefficient does not remain constant for a ratio of head-to-crest H/L > 1/3, and the actual discharge exceeds that given by the equation. Francis' experiments were made on comparatively long weirs, most of them with crest length L = 10 ft and heads in the range 0.4 ft ≤ H ≤ 1.6 ft. Thus, the equation applies particularly to such conditions. USBR experiments on 6-in, 1-ft, and 2-ft weirs has shown that the Francis equation also applies fairly well to shorter crest lengths L, provided H/L ≤ 1/3. Equation 1 is subject to the following restrictions:
|
| 131103 |