Kinematic wave

The kinematic wave is formulated by neglecting the local acceleration, advective acceleration, and pressure gradient terms of the equation of motion (e = a = p = 0). The only term that remains is the kinematic term (bottom friction and gravity) (k = 1). This wave model does not attenuate at all. It is used in the modeling of relative large flood waves, i.e., those characterized by a very small dimensionless wave number (Ponce, 2024a). In practice, the kinematic wave model is that of Seddon (1900), referred to as Kleitz-Seddon law (Chow, 1959), or simply Seddon law.

Diffusion wave

The diffusion wave is formulated by neglecting the local and advective acceleration terms in the equation of motion (e = a = 0). The remaining terms are the pressure term (p = 1) and the kinematic term (k = 1). This wave model does attenuate, albeit a small amount. It is used in the modeling of the large majority of flood waves, characterized by a small dimensionless wave number (Hayami, 1951; Ponce, 2024a).

Unnamed wave

The unnamed wave is formulated by neglecting the local acceleration and pressure-gradient terms in the equation of motion (e = p = 0). The remaining terms are the advective acceleration (a = 1) and the kinematic term (k = 1). This wave model attenuates (Ponce, 1982); however, it is not generally used in unsteady flow modeling because the neglect of only the local acceleration term (e = 0), while at the same time keeping the advective acceleration term (a = 1), is generally not warranted.

Mixed wave

The mixed wave is formulated by keeping all terms in the equation of motion (e = a = p = k = 1). This wave model amounts to the solution of the complete St. Venant equstions of unsteady open-channel flow. The mixed wave model attenuates very strongly (Ponce, 2024b). Its used is recommended particularly in the case of a dam-breach flood wave, where the suddenness of the phenomenon may justify the use of this unusual type of wave.

Dynamic wave

The dynamic wave is formulated by neglecting the kinematic term (friction plus gravity) (k = 0), while keeping the acceleration (local and advective) and pressure gradient terms in the governing equation of motion (e = a = p = 1). This wave model does not attenuate at all. It is used in the modeling of relative small waves, characterized by a very large dimensionless wave number (Ponce, 2024a). In practice, the dynamic wave model is that of Lagrange (1788), generally referred to as the Lagrange celerity equation.

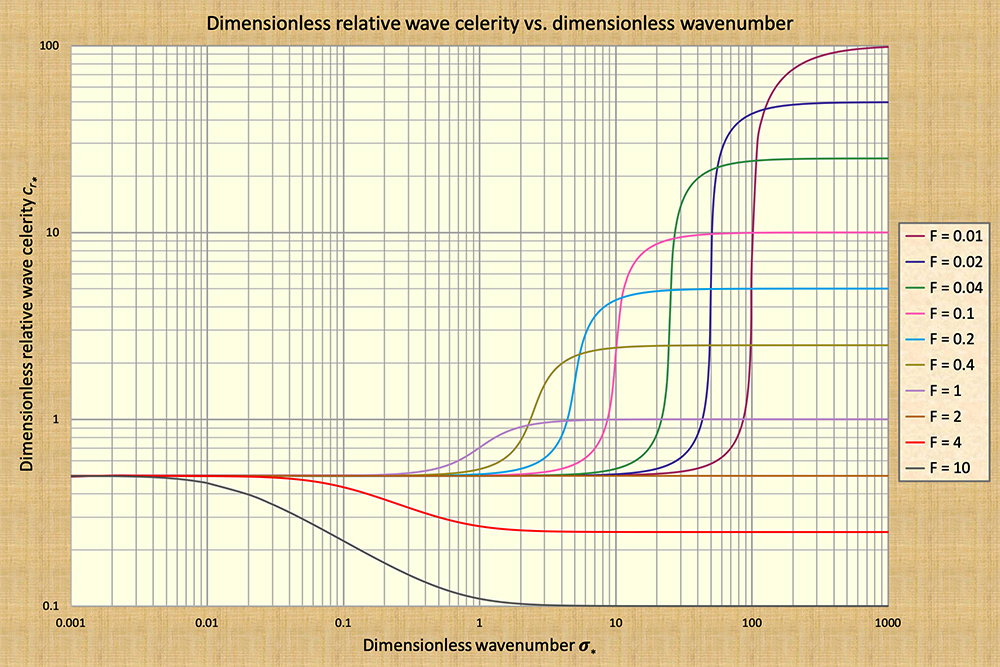
Overall assessment

A plot of dimensionless relative wave celerity vs. dimensionless wavenumber across the spectrum of shallow-water waves is showm in Fig. 2. Kinematic waves lie to the left of the wavenumber domain; dynamic waves to the right. The avowed constancy of wave celerity depicts the absence of wave attenuation. Therefore, neither kinematic nor dynamic waves attenuate!

Diffusion waves lie immediately to the right of kinematic waves (Fig. 2). They are subject to a small but appreciable attenuation. Since flood waves usually attenuate very little, diffusion waves are seen to be very applicable to the modeling of flood waves (Ponce, 2023c).

Mixed kinematic-dynamic waves, for short, mixed waves, lie towards the middle of the dimensionless wavenumber spectrum. The sharpness of the variation in dimensionless relative wave celerity with dimensionless wavenumber depicts strong to very strong wave attenuation. [Note that peak attenuation occurs at the point of inflexion, i.e., where the second derivative is equal to zero]. Figure 2 confirms the unsuitability of the mixed wave as a general basis for flood wave computations. Indeed, the mixed waves are so dissipative that they are not there for us to calculate them! Diffusion waves, on the other hand, lying toward the middle-left, precisely between kinematic (on the left) and mixed waves (at center right), are quite suited for use in modeling flood waves (Ponce, 2023b).

Ponce and Simons (1977)

Fig. 2   Dimensionless relative wave celerity cr* vs dimensionless wavenumber σ*.

What term(s) is (are) directly responsible for wave attenuation?

The unnamed wave (e = p = 0; and a = k = 1), which does attenuate (Table 1, Line A3), is not used in practice. We conclude that, unless all terms are included in the equation of motion (mixed wave, Line A4; or stable flow, Line B6), the combination of the pressure gradient term (p = 1) with the kinematic term (k = 1) is the only one responsible for wave attenuation (Lines A2, A4, and B6; note that the indicated columns are shown with light yellow background color). We also conclude that the kinematic term (k = 1) by itself does not cause wave attenuation (Line A1). In other words, we show that bottom friction and its ubiquitous partner, gravity, do not by themselves cause wave attenuation, as otherwise widely believed.

3.  FREE-SURFACE STABILITY OR INSTABILITY

A second approach to study open-channel flow wave attenuation has nothing to do with which terms are missing, or negligible, in the governing equations (this approach is contained in Table 1, Part A). Instead, in this approach all terms are present (Part B1), so that wave attenuation is not due to the presence or absence of certain terms of the equation of motion. Indeed, in unsteady open-channel flow, waves will attenuate or amplify depending on the value of the Vedernikov number V. The latter is defined as the ratio of relative celerity of kinematic waves v to relative celerity of dynamic waves u: V = v /u (Ponce, 1991; 2024b). Three situations are possible:

1. V < 1: The (primary) dynamic waves, which transport energy, travel faster than the kinematic waves, which transport mass; consequently, the flow is stable (Craya, 1952; Ponce, 1992). Stability implies that roll waves do not occur. Roll waves are periodic surface perturbations which travel downstream.

2. V = 1: The (primary) dynamic waves travel at the same speed as the kinematic waves; consequently, the flow is neutrally stable, i.e., at the onset of surface-flow instability.

3. V > 1: The kinematic waves, which transport mass, travel faster than the (primary) dynamic waves, which transport energy; consequently, the flow is unstable. Instability implies that roll waves may occur (Fig. 3).

Fig. 3   A train of roll waves traveling in a steep irrigation canal, Cabana-Mañazo, Puno, Peru.

In conclusion, open-channel flow waves will be subject to attenuation when the Vedernikov number is V < 1. In steep lined channels, when the Vedernikov number is poised to exceed 1, the attenuation factor will switch from positive to negative, setting the stage for wave amplification. This flow condition may eventually lead to the development of roll waves. We note that, depending on the discharge level, a roll wave event may or may not represent a risk of bodily harm to unsuspecting persons that are close or next to the channel when the event is occurring.

Courtesy of Jorge Molina Carpio

Fig. 4  Roll waves on the Huayñajahuira river channel, La Paz, Bolivia, on December 11, 2021.

---

4.  SUMMARY

The present article answers the question of what is the cause of wave attenuation in unsteady open-channel flow. Wave attenuation is the diffusion, dissipation, or decay of the wave amplitude upon propagation. Two approaches for analysis are recognized: (a) the modeling approach, by which one or more terms of the equation of motion are purposely omitted for the sake of modeling simplicity or mathematical tractability; and (b) the stability approach, wherein the emphasis shifts to the determination of the stability of the free surface.

In the modeling approach, four distinct models are recognized: (1) kinematic wave, (2) diffusion wave, (3) mixed kinematic-dynamic, or mixed wave, and (4) dynamic wave. In the stability approach, the focus shifts to the Vedernikov number V, wherein the flow is stable for V < 1, neutral for V = 1, or unstable for V > 1. In the modeling approach, the cause of wave attenuation is attributed to the interaction of the pressure gradient term with the kinematic term. In the stability approach, wave attenuation occurs for V < 1, and wave amplification, i.e., negative attenuation, for V > 1.

---

REFERENCES

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York, NY.

Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, National Bureau of Standards Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December, Extract.

Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, 192.

Ponce, V. M. and D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering, ASCE, 103(12), 1461-1476.

Ponce, V. M. 1982. Nature of wave attenuation in open channel flow. Journal of the Hydraulics Division, ASCE, 108(HY2), February, 257-262.

Ponce, V. M. 1991a. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M. 1992. Kinematic wave modeling: Where do we go from here? International Symposium on Hydrology of Mountainous Areas, Shimla, India, May 28-30.

Ponce, V. M. 2023a. Why is the Muskingum-Cunge the best flood routing method? Online article.

Ponce, V. M. 2023b. The Vedernikov number. Online article.

Ponce, V. M. 2023c. When is the diffusion wave applicable? Online article.

Ponce, V. M. 2024a. Kinematic waves demystified. Online article.

Ponce, V. M. 2024b. Mixed kinematic-dynamic waves debunked. Online article.

Seddon, J. A. 1900. River Hydraulics. Transactions, American Society of Civil Engineers, Vol. XLIII, 179-243, June; Extract: pages 218-223.

---