KINEMATIC WAVES DEMYSTIFIED
Professor Emeritus of Civil and Environmental Engineering
San Diego State University, San Diego,
California
1. INTRODUCTION
Kinematic waves
remain clouded in controversy (Ponce, 1991). While they have been used
in theory and practice for nearly six decades
(since the 1960's), their advantages and disadvantages are often not
completely understood by practitioners. Accordingly,
2. ORIGIN OF KINEMATIC WAVES
The theoretical foundations
of what we presently know as kinematic waves originated in the seminal
work of Lighthill and Whitham (1955),
who mathematically formulated
a certain type of wave motions which ostensibly were not dynamic in nature. Rather,
these waves could readily be construed as kinematic, since they followed purposely
from the continuity equation of one-dimensional fluid motion. Furthermore, unlike dynamic waves,
which are characteristically poised to transport energy,
kinematic waves are actually transporting mass. Different terms in the
governing equations describe each of these two waves,
kinematic and dynamic;
thus, their wave properties (celerity and attenuation) differ accordingly
(Ponce and Simons, 1977).
Boussinesq (1877) mentions Breton (1867) and Graëff (1875) as pioneers
of the theory.
Chow (1959) credits Kleitz (1877) with
being the first to derive the formula for the celerity of a kinematic wave.
3. NATURE OF KINEMATIC WAVES
Kinematic waves are flood waves; the reverse statement is also true:
Flood waves are kinematic; albeit with some exceptions which we will discuss in Section 5.
Lighthill and Whitham (1955) put it clearly when they stated, to wit:
The differences between the various types of waves in one-dimensional open-channel flow
has been
clarified by Ponce and Simons (1977).
They used linear stability theory to determine celerity and attenuation functions for
Kinematic waves are those of Seddon (1900), while dynamic waves are those of Lagrange (1877) [Note that
the latter are the "long gravity waves" referred to
by Lighthill and Whitham; see the previous paragraph]. Mixed kinematic-dynamic
waves are those lying along the middle-to-right of the
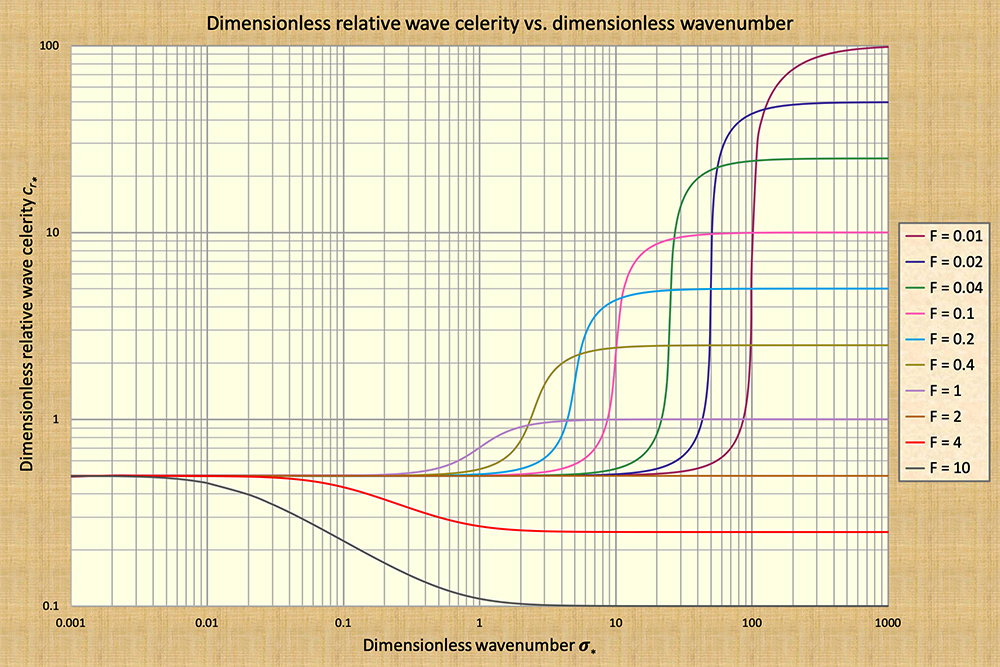
wavenumber spectrum identified by Ponce and Simons (1977) (Fig. 2).
To put it in a nutshell, Seddon's kinematic waves, lying toward the left of the dimensionless wavenumber spectrum, feature a constant wave celerity and are, therefore, nondiffusive. Following the same rationale, Lagrange's dynamic waves, lying toward the right, are also nondiffusive. However, the mixed kinematic-dynamic waves, lying toward the middle-to-right and featuring sharply varying celerity, are shown to be strongly diffusive! The amount of diffusion varies with the prevailing Froude number, with greater diffusion corresponding to the lower Froude numbers, provided the latter remains below the threshold value F = 2, applicable for Chezy friction in hydraulically wide channels (Fig. 2). To close, we reiterate that Lighthill and Whitham (1955) pointedly elaborated on the competition between kinematic and mixed waves, in order to show how completely the latter are subordinated to the former in the case of greatest practical interest, that is, when the speed of the river is well below subcritical. This underscores the general unsuitability of the mixed wave as a basis for flood wave computations and, by extension, stresses the practical importance of kinematic waves.
4. KINEMATIC-WITH-DIFFUSION WAVES
And here is where the plot tickens!
Kinematic waves are referred to as such because
they occur ostensibly in the absence of inertia, while also excluding the pressure gradient
[Table 1, Row 1].
Conversely, the (exact opposite, to judge by its components) dynamic wave
occurs significantly in the absence of only friction and gravity [Row 4].
Note that the existence of the pressure-gradient term complicates the definition of kinematic waves.
This fact led
Lighthill and Whitham (1955)
to distinguish between two types of kinematic waves:
We observe that since kinematic waves do not attenuate [Row 1], and diffusion waves do [Row 2], it follows that the pressure-gradient term must be responsible for the attenuation, i.e., the limited amount of wave diffusion experienced by typical flood waves. That this is, indeed, the case has been amply confirmed by theory and practice. We have established that dynamic (Lagrange) waves [Row 4] are too small to resemble flood waves. We have also established that mixed kinematic-dynamic waves [Row 3] are too dissipative to play a practical role in flood wave applications. Therefore, only kinematic [Row 1] and diffusion [Row 2] waves are likely to be large enough, and permanent enough, to be appropriate models of flood wave propagation.
The precise amounts of flood wave diffusion, shown in Table 2, have been
calculated by
We confirm
that kinematic waves are not subject to attenuation, although they may undergo change of shape due to
nonlinearities (Ponce and Windingland, 1985). We
also confirm that for
the midrange value of dimensionless wavenumber
σ*
> 0.17, the wave attenuation is greater than 0.30 (30%), a threshold which is widely regarded as the
limit
between diffusion waves (of limited wave diffusion, less than 30%)
and mixed waves (of unlimited wave diffusion, which could reach 1.0 (100%)
Before we wrap up the subject of kinematic waves vis-à-vis
flood waves, it remains for us to bring into the proper context the nature of
roll waves. Are these waves kinematic or dynamic? It has now been firmly
established that roll waves occur in steep lined channels
of rectangular cross-section when the kinematic wave celerity
The question as to whether a roll-wave event
may be considered a flood wave is an assessment that is best
left to the individual case. If the roll waves manage to overcome the channel boundaries, they
may be considered dangerous and, therefore, a flood wave "of sorts". Otherwise, if the roll waves remain constrained within the
channel boundaries,
within reason, they may not be taken as flood waves.
To close, we affirm that kinematic and diffusion waves find their practical application in the routing of flood waves.
Flood waves are generally massive and slow moving, unlike
dynamic (Lagrange) waves that are neither. Furthermore, mixed waves are so diffusive that they quickly disappear, with their
mass going on to join the adjacent or underlying kinematic waves, which continue to grow as they propagate downstream.
5. USES OF KINEMATIC AND DIFFUSION WAVES
Kinematic waves find their
best application in the routing of flood waves. However, they have also been used in the
routing of free-surface (overland) flows, which, due to their usually reduced scale,
may not constitute actual flood waves.
The most general application of kinematic waves
is in the routing of flood waves, that is, the numerical computer calculation of
the progression of a flood wave as it travels downstream, along a stream, river, or channel. The actual flood wave
may be a kinematic wave, with zero diffusion or, else, The distinguishing property of flood waves is that they are generally massive, and that they have little or no attenuation. In an actual field situation, the contributions of lateral inflows, from all sources, will ensure that flood waves continue to increase in mass and overall size, becoming more massive and, therefore, less attenuating, as the flood wave progresses downstream. Numerical computer models of kinematic and diffusion waves are in current use. They have been around since the 1970s, but they are not without pitfalls. Analytical solutions of the kinematic wave equation lack diffusion; numerical solutions, however, will invariably show a perceptible amount of diffusion. The latter must be attributed to the diffusion originating in the numerical scheme itself, since diffusion is absent in the (analytical) kinematic wave equation. Schemes that rely on the kinematic wave equation have no way of relating the observed numerical diffusion to the actual physical diffusion of the problem at hand (U.S. Army Corps of Engineers, 2024). Therefore, they are conceptual at best, generally falling short of the accuracy that would be expected in a mathematical model that is truly physically based. The dilemma has been resolved by Cunge (1969), who proposed a match of the numerical diffusion of the scheme itself with the physical diffusion of the related kinematic wave equation with diffusion, i.e., the diffusion wave equation. This development led to the Muskingum-Cunge method of flood routing (Ponce, 2014), an improvement on the classical Muskingum method of McCarthy (1938). The feature of grid independence, a significant asset of the Muskingum-Cunge method, sets it apart from methods based solely on the kinematic wave equation (Ponce, 1986; Ponce, 2023b). Therefore, overland flow models with diffusion wave components are clearly the next step in catchment, watershed and basin modeling (Aguilar, 2014).
6. A SINGULAR EXAMPLE
By now, surely the reader may have
become thoroughly familiar
with the nature and utility of kinematic waves, and, by extension, of diffusion waves.
All flood waves worthy of the name are subject to modeling using kinematic wave theory.
It should be obvious that the greater the basin,
the more kinematic the wave is, and the more damage may be caused by
an associated flood. Kinematic waves are not only large, but are
also slowly decaying, or attenuating, and in some cases, they lack attenuation completely (See Table 2, Row 0).
We close by focusing on the example of the anual flood wave on the Upper Paraguay river,
which drains 496,000 square kilometers in the plains of Western Central Brazil and Eastern Bolivia.
7. CONCLUDING REMARKS
We have clarified the concept of kinematic wave
and its applications in hydraulic and hydrologic engineering. We have focused on the
nature of kinematic waves and its importance as the method of choice for modeling flood waves.
Given the kinematic wave's capability to properly account for wave diffusion,
its applicability is seen to be substantially enhanced.
Competing wave types such as the mixed kinematic-dynamic and the dynamic waves of Lagrange
lack either the size (scale) and/or permanence of kinematic waves. Therefore, the kinematic wave
is regarded as the preferred method to model flood wave propagation.
REFERENCES
Aguilar, R. 2014. Diffusion
wave modeling of catchment dynamics using online calculation. M.S. thesis, Departament of Civil, Construction,
and Environmental Engineering, San Diego State University, San Diego, California, Spring.
Boussinesq. J. 1877. Essai sur la théorie de eaux courantes (Essay on the theory of running waters),
Mém. prés. Acad.Sci., Paris, 23.
Breton, Ph. 1867. Sur les barrages de retenue des graviers dans les gorges des torrents (On gravel retention dams in torrent gorges), Paris.
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York, NY.
Craya, A. 1952. The criterion for the possibility of roll wave formation.
Gravity Waves, National Bureau of Standards Circular No. 521,
National Bureau of Standards, Washington, D.C. 141-151.
Cunge, J. A. 1969. On the
Subject of a Flood Propagation Computation Method (Muskingum Method).
Journal of Hydraulic Research, 7(2), 205-230.
Flood Studies Report. 1975. Vol. III: Flood Routing Studies,
Natural Environment Research Council, London, England.
Fread, D. L. 1985. "Channel Routing," in Hydrological Forecasting,
M. G. Anderson and T. P. Burt, eds., Wiley, New York.
Graëff, J. 1875. Sur l'application des courbes de débits à l'etude du regime des rivières
(On the application of flow curves to the study of the regime of rivers),
Mém. prés. Acad.Sci., Paris, 21.
Kleitz, M. 1877. Note sur la théorie du mouvement non permanent des liquides et sur application à la propagation
des crues des rivières (Note on the theory of unsteady flow of liquids and on application to flood propagation
in rivers), Annales des ponts et chaussées, ser. 5, Vol. 16, 2e semestre, 133-196.
Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, 192.
Lighthill, M. J. and G. B. Whitham. 1955.
On kinematic waves. I. Flood movement in long rivers.
Proceedings,
McCarthy, G.T. . 1938. "The Unit Hydrograph and Flood Routing,"
unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, June 24.
(Cited by V. T, Chow's text "Open-channel Hydraulics," page 607).
Ponce, V. M. and D. B. Simons. 1977.
Shallow wave propagation in open channel flow.
Journal of Hydraulic Engineering, ASCE, 103(12), 1461-1476.
Ponce, V. N., and D. Windingland. 1985.
Kinematic shock:
Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, 111(4), April, 600-611.
Ponce, V. M. 1986.
Diffusion wave modeling of catchment dynamics.
Journal of Hydraulic Engineering, 112(8), August, 716-727.
Ponce, V. M. 1991a.
The kinematic wave controversy.
Journal of Hydraulic Engineering, 117(4), April, 511-525.
Ponce, V. M. 1991b.
New perspective on the Vedernikov number.
Water Resources Research, 27(7), July, 1777-1779.
Ponce, V. M. 1992.
Kinematic wave modeling: Where do we go from here?
International Symposium on Hydrology of Mountainous Areas, Shimla, India, May 28-30.
Ponce, V. M. 2014.
Engineering Hydrology: Principles and Practices.
Online textbook.
Ponce, V. M. 2023a.
When is the diffusion wave applicable? Online publication.
Ponce, V. M. 2023b.
Why is the Muskingum-Cunge the best flood routing method? Online publication.
Seddon, J. A. 1900. River Hydraulics. Transactions, American Society of Civil Engineers, Vol. XLIII, 179-243, June; Extract: pages 218-223.
U.S. Army Corps of Engineers. 2024.
HEC-HMS Technical Reference Manual: Synopsis of Program Methods.
Wooding, J. 1965. "A Hydraulic Model for the Catchment-stream Problem, I. Kinematic Wave Theory,"
Journal of Hydrology, Vol. 3, Nos. 3/4, 254-267.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 240321 |