1. INTRODUCCIÓN
La dicotomía entre ondas cinemáticas y dinámicas y
su relación con la escala ha desafiado una comprensión
completa en el pasado.
El tema ha sido aclarado por Ponce y Simons (1977),
quienes identificaron el número de onda adimensional apropiado y
calcularon las celeridades de onda relativas adimensionales
a través del espectro de números de onda adimensionales.
Además, aclararon las características de
varios tipos de ondas en aguas poco profundas, incluidas
sus propiedades de celeridad y atenuación. Aquí revisamos
la teoría de Ponce y Simons y explicamos su significado.
2. LA TEORÍA EXPLICADA
La teoría de ondas superficiales en el flujo
de canales abiertos se rige por las ecuaciones de
continuidad y movimiento del agua, usualmente
denominadas ecuaciones de Saint Venant
La definición apropiada de número de onda adimensional
permitió el cálculo de las funciones de celeridad
y atenuación a través de todo el dominio espacial. Los
resultados describieron la teoría
para varios tipos de ondas poco profundas,
arrojando una luz muy necesaria sobre el fenómeno.
3. FUERZAS Y TIPOS DE ONDA
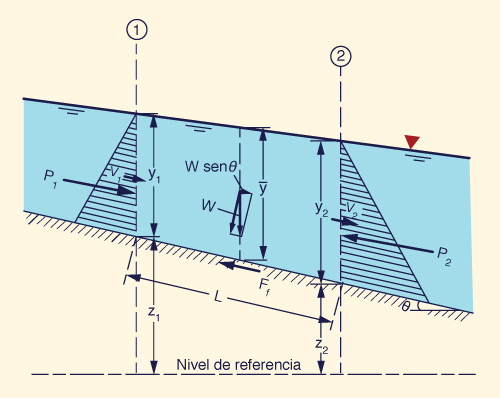
Hay cuatro fuerzas en el análisis del flujo no estacionario
en canales abiertos
(Fig. 1):
Los siguientes tipos de ondas en aguas poco profundas son de uso general: (1) cinemática, (1a) difusiva, (2) mixta cinemático-dinámica, y (3) dinámica. La onda cinemática se rige únicamente por la gravedad y la fricción (Fig. 2); la onda de difusión por gravedad, fricción y el gradiente de presiones; la onda cinemático-dinámica mixta por la gravedad, la fricción, el gradiente de presiones y la inercia (Fig. 3); y las ondas dinámicas únicamente por el gradiente de presiones y la inercia (Tabla 1).
Al principio, es necesario señalar
que actualmente existe una confusión
semántica sobre cómo llamar a los
diferentes tipos de ondas. Lo que
aquí llamamos
ondas cinemático-dinámicas mixtas
se ha denominado generalmente en la
literatura como "dinámicas", siguiendo
el trabajo de Fread (1973).
El término "onda cinemática" fue introducido por Lighthill y Whitham, supuestamente para contrastar las ondas dinámicas entonces bien establecidas, que transportan energía, con las ondas que transportan masa. Citamos aquí directamente de Lighthill y Whitham (1955):
Las ondas dinámicas clásicas transportan sólo energía; por lo tanto, se deduce que las ondas mixtas cinemático-dinámicas transportan tanto masa como energía. En la resolución de esta dicotomía reside la fuerte tendencia atenuante (disipadora) de las ondas mixtas cinemático-dinámicas.
4. CONTRIBUCIONES DE PONCE Y SIMONS Ponce y Simons graficaron celeridades de ondas relativas adimensionales en todo el espectro de números de onda adimensionales, y especializaron sus hallazgos en cada uno de los cuatro tipos de onda descritos en la Tabla 1. Crucial para este esfuerzo fue la identificación del número de onda adimensional σ* :
en la cual Lo = longitud característica del tramo, la longitud del canal en el que el flujo uniforme pierde una carga igual a su profundidad (Lighthill y Whitham, 1955):
en la cual do = profundidad de flujo uniforme constante, y So pendiente del lecho del canal. La Figura 4 muestra las celeridades de onda relativas adimensionales a través del espectro de número de onda adimensional. Dada c = celeridad de onda, la celeridad de la onda relativa cr es:
en la cual uo = velocidad del flujo uniforme. La celeridad de la onda relativa adimensional cr* es:
El rango de números de onda adimensionales mostrado en la Fig. 4 abarca seis órdenes de magnitud, desde las ondas más largas (cinemáticas, de pequeño σ*), hasta las ondas más cortas (dinámicas, de grande σ*). Aquí nos referimos a la Fig. 4 como la curva S. Los cuatro tipos de ondas (cinemática, difusiva, cinemático-dinámica mixta, y dinámica) están contenidos en la curva S.
5. ONDAS CINEMÁTICAS
Las ondas cinemáticas se rigen únicamente
por las fuerzas de gravedad y fricción. Su celeridad
es constante e igual a la celeridad de la onda
cinemática, o celeridad de Seddon, y no se
atenúan (con algunas excepciones para ondas
no lineales).
en la cual T = ancho superior del canal, Q = caudal, e y = profundidad de flujo. La celeridad de la onda cinemática se expresa alternativamente de las siguientes maneras (Ponce, 2014):
en la cual β = exponente de la curva de gasto caudal-area:
La celeridad de la onda cinemática relativa, o celeridad de la onda cinemática relativa a la velocidad del flujo, es:
La celeridad relativa adimensional de la onda cinemática es:
El valor de β es una función de la fricción del canal y la forma de la sección transversal. Para fricción de Chezy en un canal hidráulicamente ancho: β = 1,5. En este caso:
Para números de Froude en régimen
estable, F ≤ 2,
lo cual corresponde a números de Vedernikov
En la teoría de Ponce y Simons, la atenuación de la onda es una función del cambio en la celeridad relativa de la onda adimensional con el cambio en el número de onda adimensional. En otras palabras, la atenuación es causada por el cambio de celeridad con el tamaño de la onda. Para el caso de (dcr* /dσ*) = 0, no puede haber atenuación de onda; por lo tanto, las ondas cinemáticas no se atenúan.
La conclusión anterior, aunque fuerte, es
estrictamente válida solo para la teoría lineal
en canales hidráulicamente anchos. En el caso
general no lineal, las ondas cinemáticas pueden
sufrir cambios de forma, ya sea empinándose o
aplanándose, dependiendo de la forma de la sección
transversal (Ponce y Windingland, 1985).
En resumen, las ondas cinemáticas viajan con la celeridad de Seddon y, en general, no están sujetas a atenuación. La condición de que una onda sea cinemática depende del número de onda adimensional, y la onda se vuelve más cinemática a medida que σ* disminuye (consulte la Fig. 4 para conocer los valores apropiados).
El criterio para la aplicabilidad de una onda
cinemática en flujo de canal abierto ha sido
desarrollado por Ponce et al. (1978).
en la cual T = período de la onda; So = pendiente del fondo; uo = velocidad media; y do = profundidad media.
6.
ONDAS DIFUSIVAS
Las ondas difusivas se rigen por la gravedad,
la fricción y el gradiente de presiones. La inclusión
del gradiente de presiones en la formulación de una
onda difusiva proporciona difusión, es decir,
la onda es capaz de experimentar atenuación o
disipación; de ahí su nombre, onda difusiva.
El origen del nombre se remonta al trabajo
de Lighthill y Whitham (1955),
quienes consideraron que la difusión podría agregarse
a una onda cinemática al incluir el término de
gradiente de presiones en la formulación.
En la teoría de Ponce y Simons, la celeridad
de una onda difusiva es, como aproximación,
la misma que la de la onda cinemática vecina
(en el espectro de número de onda adimensional).
La diferencia está en la función de atenuación.
A diferencia de la onda cinemática, para la cual
la atenuación es cero, la onda difusiva está sujeta
a una atenuación pequeña pero finita.
Para caracterizar la magnitud de la atenuación
de la onda, Ponce y Simons utilizaron el decremento
logarítmico δ,
que mide la atenuación después de
un período de onda (sinusoidal). Para la onda de difusión,
el decremento logarítmico es:
el cual se reduce a δd ⇒ 0
cuando σ*
⇒ 0,
fusionándose así en una onda cinemática.
Una onda de difusión tiene un rango más amplio
de aplicabilidad que una onda cinemática.
En los casos en que falla una onda cinemática,
puede ser aplicable una onda de difusión.
El criterio para la aplicabilidad de una onda
de difusión ha sido desarrollado
por Ponce et al. (1978).
El criterio se basa en la siguiente desigualdad adimensional:
en la cual g = aceleración gravitacional.
En la Figura 4, las ondas difusivas caerían a
la derecha de las ondas cinemáticas, en el medio
del rango adimensional del número de onda,
0.1 ≤ σ* ≤ 10,
dependiendo del número de Froude.
7.
ONDAS CINEMÁTICO-DINÁMICAS MIXTAS
Las ondas cinemático-dinámicas mixtas están gobernadas
por las cuatro fuerzas: gravedad, fricción, gradiente
de presiones, e inercia. Como tal, una onda mixta
cinemático-dinámica representa la
formulación más
completa de ondas de poco profundas en flujo
en canales abiertos; sin embargo, no está exenta
de problemas. En condiciones típicas de flujo subcrítico,
las ondas cinemático-dinámicas mixtas están sujetas
a una atenuación muy fuerte, hasta el punto de que a
menudo se puede cuestionar su existencia. Este hecho
fue reconocido por Lighthill y Whitham (1955) cuando afirmaron:
Por lo tanto, las ondas mixtas cinemático-dinámicas, que se encuentran directamente en la rama ascendente de la curva S (Fig. 4), generalmente están sujetas a una atenuación muy fuerte. La tasa de atenuación aumenta con la rapidez de ascenso de la curva, alcanzando su pico en el punto de inflexión. Estas proposiciones fueron demostradas por Ponce y Simons (1977) en su análisis del modelo de onda mixto cinemático-dinámico. Los resultados se resumen en las Figs. 4, 6, 7 y 8.
Las siguientes conclusiones se extraen de la Fig. 4:
Las siguientes conclusiones se extraen de la Fig. 6:
Las siguientes conclusiones se extraen de la Fig. 7:
Las siguientes conclusiones se extraen de la Fig. 8:
En resumen, los hallazgos de Ponce y Simons (1977)
sirven para esclarecer la relación entre
ondas cinemáticas y
cinemático-dinámicas mixtas: Mientras las
primeras no se atenúan,
8.
ONDAS DINÁMICAS
Las ondas dinámicas de la mecánica clásica se rigen
únicamente por el gradiente de presiones y la inercia.
Se encuentran a la derecha del espectro de número de onda
adimensional, correspondiente a la parte superior de la
curva S de la Fig. 4.
En su mayor parte, su celeridad es constante e igual a
la celeridad de la onda dinámica, o celeridad clásica
de Lagrange, expresada de la siguiente manera:
Esta ecuación revela los dos componentes de la
onda dinámica. La celeridad relativa de la
onda dinámica es:
La celeridad relativa adimensional de la onda dinámica es:
el cual se reconoce como el recíproco del número de Froude:
La Ecuación 17 se representa en la Figura 4.
Por ejemplo, para F = 0,1 (curva rosada),
el valor de la celeridad de onda relativa adimensional
se aproxima a 10 a la derecha de la escala.
Las siguientes conclusiones con respecto a las ondas dinámicas se extraen de la Fig. 4:
9.
RESUMEN
Se revisa y esclarece la teoría de ondas
superficiales de Ponce y Simons (1977), con
el objetivo de mostrar su importancia en el esclarecimiento de
la mecánica del flujo no estacionario en canales abiertos.
Se identifican
BIBLIOGRAFÍA
Fread, D. L. 1973. Technique for implicit dinámicas routing in rivers with tributaries. Water Resources Research,
9(4), 338-351.
Lagrange, J. L. 1788. Mécanique analytique, Paris, part 2, section II, article 2, p. 192.
Lighthill, M. J., y G. B. Whitham. 1955.
On cinemáticas waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
Ponce, V, M., y D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.
Ponce, V, M., R. M. Li, y D. B. Simons. 1978.
Applicability of cinemáticas y difusión models. Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, March, 353-360.
Ponce, V. M., y D. Windingland. 1985. Kinematic shock: Sensitivity analysis,
Journal of Hydraulic Engineering, ASCE, 114(4), 600-611.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V. M. 2014.
Engineering hydrology: Principles y practices. Second edition, online textbook.
Ponce, V. M. 2014.
Fundamentals of Open-channel Hydraulics. Online textbook.
Ponce, V. M. y B. Choque Guzmán. 2019.
The control of roll waves in channelized rivers. Link No. 36023
in ponce.sdsu.edu.
Seddon, J. A. 1900. River hydraulics.
Transactions, ASCE,
Vol. XLIII, 179-243, June.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 251031 |