|
| |
The control of roll waves
in channelized rivers
Víctor Miguel Ponce
and
Beatriz Choque
Guzmán
13 June 2019
|
|
|
Abstract.
The theoretical foundations and relevant experience with open-channel flow instability are
examined with the objective of controlling roll waves.
The latter seem to recur with relative frequency in channelized rivers where the Vedernikov number has
increased, due to the channelization, above the threshold V = 1 .
It is shown that β, the exponent of the discharge-flow area rating,
is of paramount importance in the control
of roll waves.
Several examples show conclusively the existence of a definite relation between β and V, namely,
that as the cross-sectional shape departs from rectangular, β decreases accordingly, resulting in a drop
in the value of V.
A sufficient decrease in β will
cause V to drop below the threshold of flow instability.
The methodology developed herein is applied to two channelized rivers in La Paz, Bolivia,
where large roll waves have recently been recurring with
increasing frequency.
The analysis confirms
that the channelized rivers where roll waves
have occurred have done so under β > 1.6 and V > 1.
The results
underscore the promise of β
analysis in the design of channelized rivers with the objective of controlling roll waves.
|
1. INTRODUCTION
The occurrence of roll waves in open-channel flow continues to attract the interest of
researchers and laypersons alike. In 1907, Cornish showed,
for the first time, a
photograph of the fascinating phenomenon in a paper published in the Journal of the Royal
Geographical Society (Fig. 1) (Cornish, 1907). Later, in Chapter 8 of his
authoritative textbook, Ven Te Chow referred to the phenomenon
as the "instability of uniform flow," implying that under certain conditions the
flow could become unstable and break
into a train of waves (Chow, 1959).
A contemporary photograph of the roll wave phenomenon is shown in Fig. 2.
Fig. 1 Early photograph of a train of roll waves in the Swiss Alps (1907).
|
Fig. 2 Roll waves in a lateral irrigation canal, Cabana-Mañazo irrigation,
Puno, Peru (2007).
|
A roll-wave event is an unusual and often fascinating phenomenon, to be admired
by those fortunate enough to observe it.
However, under the proper set of circumstances, it could be disturbing and even
dangerous. Therefore, it is imperative for hydraulic engineers to understand the
principles governing the formation and propagation of roll waves,
so that channel design
may aim to minimize possible
negative impacts to society.
In this article, we focus on the case study in La Paz, Bolivia, where roll waves
have been documented to recur with troubling frequency in certain channelized rivers.
Locally, these often large roll waves
are referred to as pulsating waves. La Paz,
a city of about 800,000 people and the seat of the plurinational state
of
Bolivia, features a peculiar geomorphological setting:
It is almost entirely
built inside an inmense gully,
with several steep-gradient streams draining its eastern side toward the center (Fig. 3).
Fig. 3 Panoramic view of La Paz, Bolivia, shown
built inside a huge gully.
|
Over the past 30 years, urban development has resulted in the channelization of several of the
main tributary streams with masonry-lined channels, intended to convey high waters in the most
efficient hydraulic way.
However, as constructed, the drainage
canals have modified the conveyance cross-section so that
roll-wave events are now recurrent (2019), where they did not exist prior to channelization.
With the menace of global warming
upon us, it is expected that the intensity and frequency of these events will increase in time, thus necessitating
a renewed and bolder approach to their management.
By way of illustration, we show two videos taken in La Paz in recent years.
The first video shows a roll-wave event on the Achumani river, a
tributary of the La Paz river (Fig. 4). This event occurred in 2014.
The video allows the estimation of the
wave period as 19 seconds.
|
[Click on top of photo to watch video]
|
Fig. 4 The channelized Achumani river, La Paz, Bolivia (2014).
|
The second video shows a roll-wave event on the Huayñajahuira river, another tributary
of the La Paz river, in February 24, 2016. In this case, the pulsating flow is seen to be large enough to
jump over the top of the channel, constituting a
public safety hazard (Fig. 5).
At the present time (2019), this type of event
continues to recur in these two
channelized rivers, clamoring for a solution to the problem.
|
[Click on top of photo to watch video] |
Fig. 5 The channelized Huayñajahuira river, La Paz, Bolivia (2016).
|
In this article, we review the historical background and examine relevant theory, experience,
and possible solutions to control, attenuate, and/or manage these waves so that
society may be assured that they will cause no
harm to people or damage to property.
2. HISTORICAL BACKGROUND
In 1945, V. V. Vedernikov presented, in the Russian language, a thorough mathematical analysis of roll waves
(Vedernikov, 1945; 1946). At about the same time, A. Craya published a paper on flow instability
in the French journal La Houille Blanche (Craya, 1945).
However, Craya's definitive work on the subject of flow instability
was published only seven years later
(Craya, 1952).
In a paper published in the Transactions of the American Geophysical Union,
Ralph W. Powell christened the Vedernikov criterion as the Vedernikov number
(Powell, 1948). Later, Ven Te Chow confirmed the practice
in his well-respected textbook (Chow, 1959).
Craya clarified the Vedernikov criterion interpreting it as the threshold
at which the celerity of kinematic waves equals the celerity of dynamic waves.
As early as 1900, Seddon, working on the Lower Mississippi river,
had derived the expression for the celerity of kinematic waves, i.e., waves governed
solely by friction and gravity (Seddon, 1900). Later, Lighthill and Whitham (1955) elaborated on the
theoretical and mathematical foundations of kinematic waves, highlighting their
application to the propagation of flood waves.
In contrast to a kinematic wave, the dynamic wave of classical fluid mechanics,
traveling with the Lagrange celerity, is a wave
governed solely by inertia and the pressure gradient (Lagrange, 1788).
We note that Lagrange's relative dynamic wave celerity is
the denominator of the well-known Froude number
(Ponce, 2014: Chapter 1).
Ponce (1991)
presented a unified theoretical treatment of the Froude and Vedernikov numbers, showing them to be essentially
independent of each other. The analysis followed on earlier seminal work by
Ponce and Simons (1977), which
laid the foundation for the complete analysis of unsteady open-channel flow
across the dimensionless wavenumber
spectrum. Ponce confirmed Craya's earlier finding regarding the threshold of flow instability
as the instance when the
mass waves of Seddon (i.e.,
the kinematic waves) overcome the energy waves of Lagrange (the dynamic waves).
This threshold occurs when the kinematic wave celerity equals or exceeds
the dynamic wave celerity, i.e.,
when the Vedernikov number V ≥ 1.
Therefore, the nature of roll waves is intrinsically connected to the concept of
Vedernikov number.
3. THE VEDERNIKOV NUMBER
Ponce (1991)
and more recently,
Ponce (2014)
identified
three velocities of interest in unsteady open-channel flow:
The velocity u of the steady uniform flow, which may be calculated by a
formula such as Manning or Chezy;
The relative celerity v
of kinematic waves, defined as v =
ck - u, where ck is the celerity of
kinematic waves; and
The relative celerity w
of dynamic waves, defined as w =
cd - u, where cd is the celerity of
dynamic waves.
The following hydraulic variables are defined:
|
Definition of hydraulic variables
Discharge: Q
Flow area: A
Mean velocity: u = Q / A
Wetted perimeter: P
Top width: T
Hydraulic radius: R = A /P
Hydraulic depth: D = A /T
Discharge-flow area rating curve: Q = α A β
Gravitational acceleration: g
Kinematic wave celerity
(Ponce, 2014: Chapter 1): ck = β u
Relative kinematic wave celerity: v = ck - u = (β - 1) u
Dimensionless relative kinematic wave
celerity: v / u = β - 1
Dynamic wave celerity (Ponce, 2014): cd = u ± (gD)1/2
Relative dynamic wave celerity: w = cd - u = (gD)1/2
Dimensionless relative dynamic wave
celerity: w / u = (gD)1/2 / u = 1 / F
Froude number: F = u / w = u / (gD)1/2
Vedernikov number: V = v / w = (β - 1) u / (gD)1/2
|
Therefore, there are only three characteristic velocities in the present
analysis: u, v, and w.
The Froude number is the ratio of the first and the third: F = u / w;
the Vedernikov number is the ratio of the second and the third: V = v / w.
It is clearly seen that the Froude and Vedernikov numbers are independent of each other; the three velocities give
rise to only two independent dimensionless numbers, the Froude and Vedernikov numbers. The third ratio
is the dimensionless relative kinematic wave celerity v / u = β - 1
= V / F.
Thus, the exponent of the rating β subsums both V and F.
It follows that:
and, consequently, the discharge-flow area rating may be expressed in terms of the Froude and Vedernikov numbers as follows:
In summary,
the Froude number is the ratio of the velocity of the flow to the relative celerity of dynamic waves.
For F < 1, subcritical flow conditions prevail and surface perturbations are able to travel upstream,
making possible downstream control. For F > 1, supercritical flow conditions prevail and
surface perturbations are not able to travel upstream; therefore,
the flow could be controlled
only from upstream. The Froude criterion is strictly applicable to steady uniform flow, although in practice
its usage has been extended to other flow conditions.
The Vedernikov number is the ratio of the relative celerity of kinematic waves
to the relative celerity of dynamic waves.
As such, the Vedernikov criterion is strictly applicable to unsteady flow. For V < 1,
dynamic waves travel faster than kinematic waves and, consequently, the flow is stable, i.e., free from roll waves.
Conversely, for V > 1,
kinematic waves travel faster than dynamic waves and, consequently, the flow is unstable, i.e., subject to the
occurrence of roll waves. However, whether roll waves actually occur will depend on the boundary
conditions (See Section 5).
Thus, the Vedernikov criterion is seen to be necessary, but not sufficient, for the occurrence of roll waves.
The roles of mass and energy are central to the analysis of roll waves.
It is well established that while
kinematic waves transport mass, dynamic waves transport energy
(Lighthill and Whitham, 1955). Therefore,
the occurrence of roll waves is seen to be related to the unsteady
transport of mass overcoming the unsteady transport of energy.
In this light,
roll waves are a curious physical manifestation of the preponderance of mass transport
over energy transport in unsteady open-channel flow.
4. EFFECT OF CROSS-SECTIONAL SHAPE
The Vedernikov number is:
V = (β - 1) u / (gD)1/2
| (3) |
While hydraulic engineers are very familiar with the Froude number,
a similar statement does not follow
for the Vedernikov number, which continues to be largely ignored, or
set aside, in hydraulic engineering practice
(Ponce, 2002).
To focus on the more familiar Froude number, the Vedernikov number may be expressed as follows:
Equation 4 shows that the Vedernikov number and the related flow instability are determined
by the product of (β - 1) times
the Froude number F. In practice, the Froude number does not vary through a wide range; therefore, (β - 1) is the controlling factor in flow instability.
According to theory, neutral stability, i.e.,
the threshold of flow instability, corresponds to V = 1.
From Eq. 4, the Froude number
for neutral stability is:
To unravel the physical meaning of flow instability, it is necessary to examine the true nature of
β,
the exponent of the discharge-area (Q - A) rating. Essentially, β is the ratio of kinematic
wave celerity ck to mean flow velocity u. In other words, β
is the factor by which to multiply the mean flow velocity to obtain the kinematic wave celerity.
For β ≡ 1, the kinematic wave celerity is equal to the mean flow velocity,
averting flow instability.
The value of β is a function of type
of boundary friction and cross-sectional shape. In practice,
boundary friction may be either:
Laminar;
Mixed laminar-turbulent; or
Turbulent.
Turbulent flow may be expressed in terms of either the
Manning or Chezy equations.
The cross-sectional shape may vary widely, and with it,
the value of β. There are
three asymptotic cross-sectional shapes,
in terms of the applicable values of β
(Ponce, 2014: Chapter 1):
Hydraulically wide, with constant wetted perimeter P;
Triangular, for which the top width T is proportional to the maximum flow depth d;
Inherently stable, with constant hydraulic radius R
(Ponce and Porras, 1995).
Table 1 shows the values of β corresponding
to selected combinations of boundary friction and cross-sectional shape.
Following Eq. 5, the values of neutrally stable Froude number
Fns
are shown in the last column. The practical range
of β values shown is: 1 ≤
β ≤ 3, with the higher value (β = 3)
corresponding to (hydraulically wide) laminar flow (i.e., surface flow on a plane) and the
lower value (β = 1)
to the inherently stable cross-sectional shape.
We credit Liggett (1975) with pioneering the theory of the stable channel.
| Table 1 Values of Fns for selected
values of β.
|
| β |
Type of friction |
Cross-sectional shape |
Fns |
| 3 |
Laminar |
Hydraulically wide |
1/2 |
| 8/3 |
Mixed laminar-turbulent (25% turbulent Manning) |
Hydraulically wide |
3/5 |
| 21/8 |
Mixed laminar-turbulent (25% turbulent Chezy) |
Hydraulically wide |
8/13 |
| 7/3 |
Mixed laminar-turbulent (50% turbulent Manning) |
Hydraulically wide |
3/4 |
| 9/4 |
Mixed laminar-turbulent (50% turbulent Chezy) |
Hydraulically wide |
4/5 |
| 2 |
Mixed laminar-turbulent (75% turbulent Manning) |
Hydraulically wide |
1 |
| 15/8 |
Mixed laminar-turbulent (75% turbulent Chezy) |
Hydraulically wide |
8/7 |
| 5/3 |
Turbulent Manning |
Hydraulically wide |
3/2 |
| 3/2 |
Turbulent Chezy |
Hydraulically wide |
2 |
| 4/3 |
Turbulent Manning |
Triangular |
3 |
| 5/4 |
Turbulent Chezy |
Triangular |
4 |
| 1 |
Any |
Inherently stable |
∞ |
The central value of the feasible range of β, corresponding to turbulent flow in a hydraulically wide
channel is β = 5/3 for Manning friction
and β = 3/2 for Chezy friction.
The corresponding values of dimensionless relative kinematic wave celerity (β - 1) are 2/3 for
Manning, and 1/2 for Chezy. Therefore, under Manning friction in a hydraulically
wide channel, a kinematic wave travels with a speed that is about 2/3 faster than the
mean flow velocity; likewise, under Chezy friction, it is 1/2 faster.
The value of β = 1, corresponding to the inherently stable channel, merits further
elaboration. In this case, the Froude number for neutral stability is Fns = ∞.
However, in practice, the maximum value of Froude number is limited by frictional considerations, with
its value not likely to exceed 30 in the worst case. Thus, the inherently stable channel is at best a theoretical construct:
There is no need to built an inherently stable channel, applicable for a Froude number
that surely will never be realized.
Alternatively, it makes sense to design a channel for a finite value of Fns,
carefully chosen as a physically realistic value that the flow is not likely to exceed
(Ponce and Diaz, 2016).
For such a conditionally stable channel, the applicable value of β
may be calculated by Eq. 6.
For instance, for Fns = 25, Eq. 6 gives β = 1.04.
Therefore, values of β in excess of 1 but close to it are sufficient
to assure stability within a range of practical
neutral-stability Froude numbers (2.5 ≤ Fns ≤ 25).
Table 2 shows values of β
suitable for design. For instance, for a cross-section with
β = 1.2,
the flow will become unstable as the Froude number exceeds 5.
|
Table 2 Values of β for selected
values of Fns.
|
| Fns |
β |
|
Fns |
β |
| 2.5 |
1.40 |
|
10 |
1.10 |
| 3 |
1.33 |
|
12 |
1.08 |
| 4 |
1.25 |
|
15 |
1.07 |
| 5 |
1.20 |
|
20 |
1.05 |
| 8 |
1.12 |
|
25 |
1.04 |
In summary, it is shown that β,
the exponent of the discharge-area rating (Eq. 2) and a characteristic of the
cross section,
is largely responsible for the occurrence of roll waves in unsteady open-channel flow.
Further analysis shows, however, that the β condition may be necessary but not sufficient.
As shown by Ponce and Simons (1977), in turbulent open-channel flow,
across the spectrum of dimensionless wave numbers, certain values of the latter
are likely to amplify waves more than others. This proposition is further discussed
in the following section.
5. SHALLOW WAVE PROPAGATION
The necessary and sufficient condition for roll wave formation may be analyzed using the theory
of shallow wave propagation of Ponce and Simons (1977). These authors applied the method of linear stability
to the set of equations governing unsteady open-channel flow, commonly referred to as the St. Venant equations. The analysis led to
celerity and attenuation functions of various types of
shallow-water waves, including kinematic, diffusion, mixed kinematic-diffusion,
and dynamic (Ponce, 2014: Chapter 10).
The findings are summarized in Figs. 6 to 8.
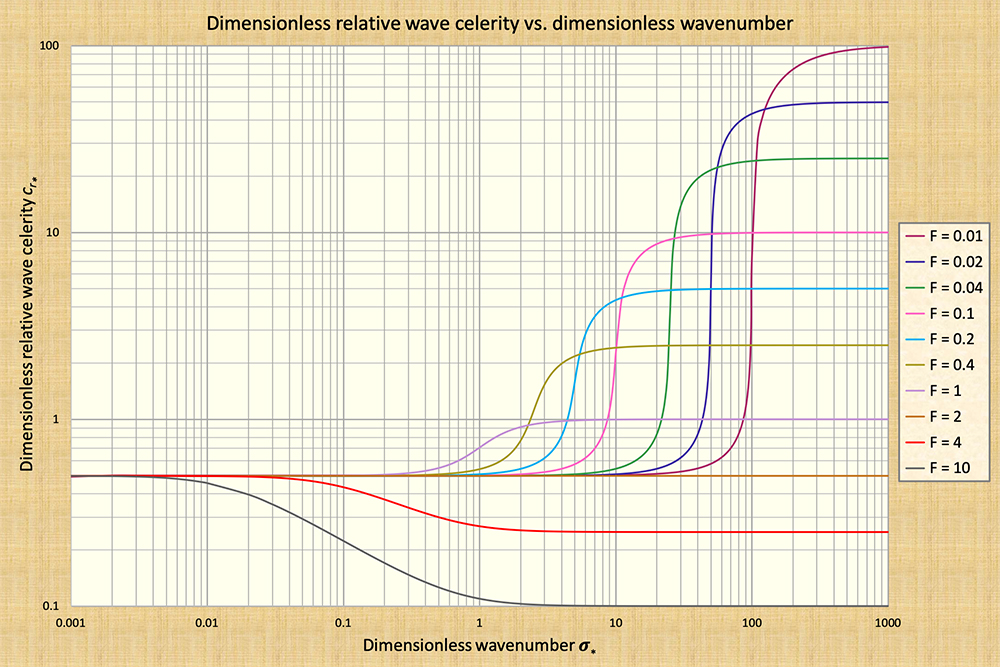
Figure 6 shows values of dimensionless relative wave celerity cr*
(ordinates) across a wide range of dimensionless wavenumbers σ* (abscissas).
This figure shows that cr* ⇒ 0.5 as σ* ⇒ 0
in the kinematic range (to the left); conversely, cr* ⇒ (1/ F)
as σ* ⇒ ∞ in the dynamic range (to the right).
As expected, for midrange values of dimensionless wavenumbers,
cr* is shown to vary strongly with wavenumber, the variation being increasingly marked as the
Froude number decreases.
Admirably, Fig. 6 confirms the validity of the Seddon formula toward the left of the graph and of the Lagrange formula toward the right.
Figure 6 also shows that for F = 2, cr* is constant and equal to 0.5, which corresponds to the value
of neutrally stable Froude number (V = 1) for a hydraulically wide channel with Chezy friction (Table 1). Therefore, for F = 2, all wave scales travel with the
same celerity, confirming the validity of the Vedernikov theory.
Wave attenuation or amplification is produced when the value of cr* varies across the dimensionless wavenumber spectrum.
It can be shown that neither Seddon waves (kinematic) nor Lagrange
waves (dynamic) are subject to (any amoiunt of) attenuation or amplification.
Figure 6 describes wave attenuation for F < 2 (i.e., for a positive cr* gradient)
and wave amplification for F > 2 (for a negative cr* gradient), again confirming the validity of the Vedernikov theory.
Fig. 6 Dimensionless wave celerity vs. dimensionless wavenumber in unsteady open-channel flow.
|
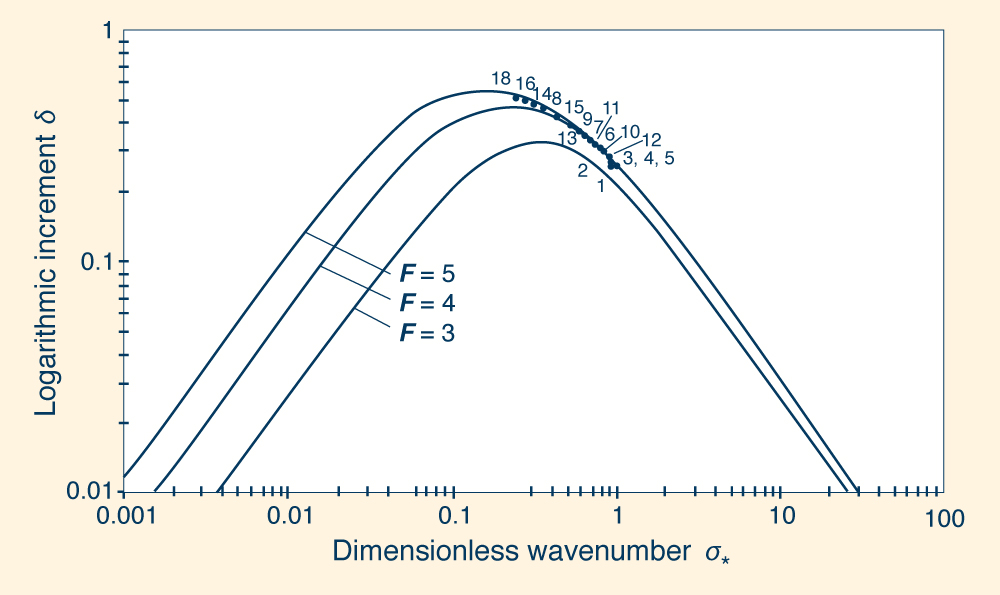
Figure 7 shows values of logarithmic decrement δ
(in the ordinates) across a wide range of dimensionless wavenumbers
σ* (abscissas), for Froude
numbers in the range 0.01 ≤ F ≤ 1.5.
[The value F = 2 has zero attenuation; therefore, it could not be plotted on a log scale].
In direct correspondence with Fig. 6, in Fig. 7 wave attenuation is shown to be more marked as the
Froude number decreases to F = 0.01.
Predictably,
the peak attenuation is seen to match the point of inflection in the
cr* vs.
σ*
curves of Fig. 6. It is confirmed that wave attenuation decreases toward either
extreme of the wavenumber spectrum, with -δ ⇒ 0 for both
σ* ≤ 0.001 (kinematic waves) and
σ* ≥ 1000 (dynamic waves).
Fig. 7 Logarithmic decrement -δ vs. dimensionless wavenumber σ*
in unsteady open-channel flow: 0.01 ≤ F ≤ 1.5.
|
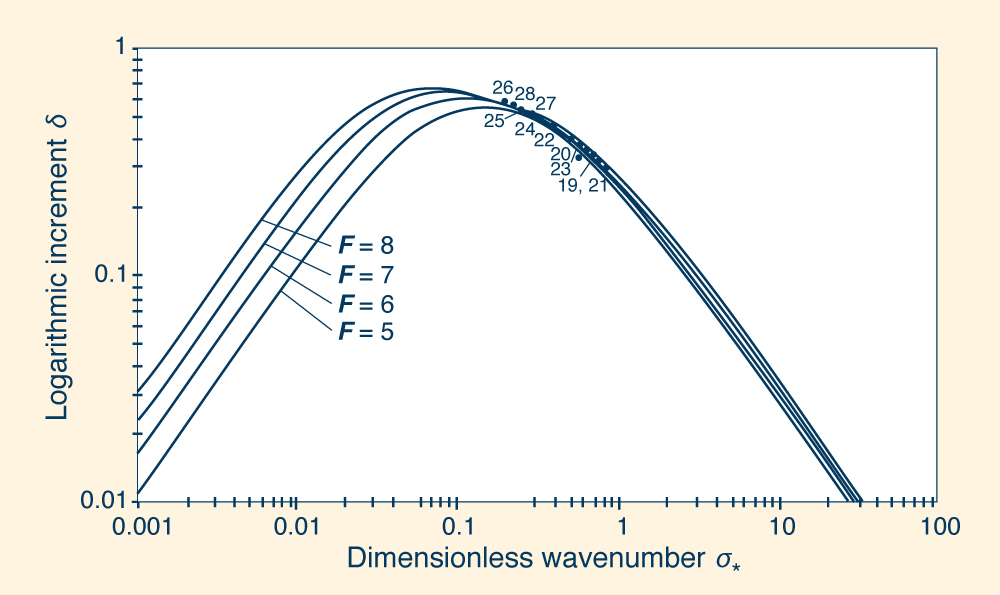
Figure 8
shows values of logarithmic increment +δ
(ordinates) (i.e., wave amplification) across a wide range of dimensionless wavenumbers
σ* (abscissas), for Froude
numbers in the range 3 ≤ F ≤ 10.
In direct correspondence with Fig. 6, wave amplification is shown to be somewhat
more marked as the
Froude number increases from F = 3 to F = 10.
Predictably,
the peak attenuation is seen to match the point of inflection in the
cr* vs.
σ*
curves of Fig. 6. It is confirmed that wave amplification decreases toward either
extreme of the wavenumber spectrum, with +δ ⇒ 0 for both
σ* ≤ 0.001 (kinematic waves)
and σ* ≥ 1000 (dynamic waves).
Fig. 8 Logarithmic increment +δ vs. dimensionless wavenumber σ*
in
unsteady open-channel flow: 3 ≤ F ≤ 10.
|
The foregoing analysis has confirmed that wave amplification will occur for Froude numbers F > 2, which corresponds with Vedernikov number
V > 1 for the case of Chezy friction in a hydraulically wide channel.
As shown in Table 1, for the case of Manning friction, the condition V > 1 corresponds to F > 1.5.
In practice, flow instability, corresponding to a positive value of δ,
may start to occur with Froude numbers as low as 1.5 (under Manning friction)
Practical experience suggests that the Vedernikov criterion (V ≥ 1) is necessary but not sufficient
for the occurrence of roll waves. Roll waves do not occur all the time in steep channels where the
instability criterion is met. In fact, roll waves are seen to be an unusual occurrence.
In summary, the Ponce and Simons (1977) theory of shallow wave propagation
confirms Vedernikov's theory.
Most significantly, for Froude numbers in the unstable regime,
the value of the logarithmic increment δ (refer to Fig. 8) is not constant,
peaking at the point of inflection of the dimensionless relative celerity vs. dimensionless wavenumber
function (refer to Fig. 6). This fact clearly establishes a
preferential dimensionless wavenumber range for the amplification of open-channel flow
disturbances
into roll waves.
6. EXPERIMENTAL
VERIFICATION
Figure 8 shows the range of dimensionless wavenumbers
where the wave amplification is likely to be stronger. In fact, there is a value of
σ* for which the logarithmic increment +δ is a maximum.
Figure 8 shows that for F = 4 (the red curve), +δpeak = 0.5
corresponds to
σ*@peak = 0.22.
The wave amplification is assured by the nature of the variation of the
dimensionless relative wave celerity for
F > 2 in Fig. 6. For F = 4, peak
wave amplification occurs at the point of inflection of the red curve of Fig. 6,
for which σ*@inflection = 0.22.
Note that this value is equal to the σ*@peak = 0.22
of Fig. 8.
Therefore, the existence of a
preferential dimensionless wavenumber range for roll wave propagation is confirmed.
To verify the theory, Ponce and Maisner (1993) used the classical Brock laboratory
flume data, developed at the California Institute of Technology.
Brock (1967) measured crest depths and wave periods of roll waves under a
wide range of flow conditions. Ponce and Maisner compared experimental dimensionless wavenumbers,
calculated from wave periods measured by Brock,
with dimensionless wavenumbers predicted by the theory.
Note that the correct theory would show that the laboratory data plots at or near the peak of the curves shown in Fig. 8.
The results of the comparison are shown in Fig. 9.
It is observed that Brock's data agrees reasonably well with the theory.
All measured data is shown to plot near the peaks of the
theoretical logarithmic increment vs. dimensionless wavenumber curves.
Therefore, the roll-wave component of the theory of shallow wave propagation
has been experimentally verified.
Fig. 9 (a) Comparison of theoretical and experimental dimensionless wavenumbers
for Froude numbers in the range 3 ≤ F ≤ 5.
|
Fig. 9 (b) Comparison of theoretical and experimental
dimensionless wavenumbers
for Froude numbers in the range
5 ≤ F ≤ 8.
|
7. WAVE DIFFUSION VS. WAVE AMPLIFICATION
Roll waves, occurring under unstable flow, are one of the manifestations of unsteady
flow in open channels (V > 1).
The other are kinematic waves and dynamic waves
occurring under stable flow (V < 1).
Under unsteady flow, waves are created in an open channel by action of
the boundary conditions and other flow irregularities. Once in the channel, the various scales (sizes) of
waves will either: (a) attenuate, (b) hold their stage, or (c) amplify.
Theory confirms that waves will: (a) attenuate for V < 1;
(b) hold their stage for V = 1; and amplify for
V > 1 (Section 3).
The Vedernikov criterion V = 1 is an absolute criterion and, therefore,
independent of the type of friction or cross-sectional shape.
It may be alternatively expressed as
Fns, i.e., the Froude number corresponding to
V = 1
(Section 4).
Table 1 shows that Fns varies with the type of friction and cross-sectional shape.
For instance,
Fns = 2 for
Chezy friction in a hydraulically wide channel, Fns = 4
for Chezy friction in a triangular channel,
and Fns = ∞
for an inherently stable channel, regardless of the type of friction.
It is observed that
Fns increases with the decrease of β as the cross-sectional
shape departs from hydraulically wide; in the limit,
for β ⇒ 1,
Fns ⇒ ∞.
Whether a wave diffuses or amplifies will depend on: (1) the effect of boundary friction, and (2)
the effect of cross-sectional shape. For V < 1, all waves will attenuate.
The strength of the attenuation will depend on the Froude number (of the steady uniform flow) and
the dimensionless wavenumber of the perturbation, with lower Froude numbers undergoing markedly
greater attenuation (Fig. 7).
Wave attenuation peaks near the midrange (and
right of midrange) of dimensionless wavenumbers.
For V > 1, all waves will amplify.
The strength of the amplification will depend on the Froude number and
the dimensionless wavenumber of the perturbation, with higher Froude numbers undergoing somewhat
greater amplification (Fig. 8).
Wave amplification peaks near the midrange (and left of midrange) of dimensionless wavenumbers.
The strength of the wave diffusion or amplification is related to the rate of variation
of dimensionless relative wave celerity with dimensionless wavenumber (Fig. 6). In the stable regime
(V < 1),
this rate of variation increases markedly as the Froude number decreases,
increasing the rate of attenuation (Fig. 7).
Conversely, in the unstable regime (V > 1),
the rate of variation
increases mildly as the Froude number increases,
mildly increasing the rate of amplification (Fig. 8).
The exponent of the rating β
conditions and produces attenuation or amplification at any scale in the wavenumber spectrum.
Values of
β ⇒ 5/3 for Manning friction (and β ⇒ 3/2 for Chezy)
lead to wave amplification.
This is because wave transport being nonlinear,
the wave peaks are able to travel
faster than the mean flow, with the wave faces poised to steepen
and eventually break. Conversely, values of β ⇒ 1
(i.e., approaching 1) lead to wave attenuation, i.e., wave diffusion,
because the wave peaks are traveling at nearly the same
speed as that of the mean flow and,
therefore, are poised not to steepen.
In conclusion, managing β (at the design stage) is a
sure way to control flow amplification and thus, avert flow instability.
A hydraulically wide channel features β ⇒
5/3 for Manning friction (and β ⇒ 3/2 for Chezy);
therefore, it is preeminently not conducive to wave diffusion. Moreover,
a rectangular
channel cross-section is that closest to hydraulically wide,
with typical values
of β in the range 3/2 to 5/3. Therefore, a rectangular cross section
is also not
conducive to wave diffusion.
Values of β ≤ 4/3 for Manning
(or β ≤ 5/2 for Chezy) are more
conducive to wave diffusion since they raise the value of
Fns above 3 or 4 (Table 1), discouraging
flow instability.
8. CALCULATION OF β
It has been shown that β, the exponent of the discharge-flow area
rating, a characteristic of the shape of the cross section, determines to a large extent
whether the flow may become unstable or not. A value of β = 5/3, corresponding to a
hydraulically wide channel (Manning),
more readily leads to flow instability.
As β decreases to 4/3, i.e., for a triangular channel (Manning),
a larger Froude number is required to
produce flow instability, in effect discouraging the latter.
As β ⇒ 1, flow instability is no longer possible.
Therefore, it is imperative that steep channels (under supercritical flow)
be designed by paying close attention to
β.
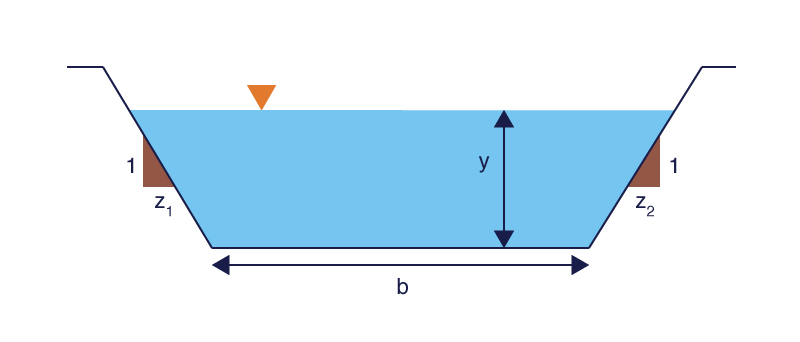
The
online script
onlinechannel15b calculates
β for a prismatic channel of trapezoidal, rectangular, or triangular cross
section (Fig. 10).
The calculator requires the following input:
Input to onlinechannel15b:
-
Bottom width b
-
Flow depth y
-
Side slope z1
-
Side slope z2
-
Manning's n
-
Bottom slope S.
|
Fig. 10 Definition sketch for a cross section of trapezoidal,
rectangular, or
triangular shape.
|
To demonstrate the online calculator, we consider two examples: (1) a rectangular
cross section, and (2) a trapezoidal cross section; to pass an arbitrary discharge of Q = 50 m3/s.
In Example No. 1, assume b = 5.8 m,
y = 1.066 m, z1 = 0, z2 = 0,
n = 0.025, and S
= 0.057. The output from onlinechannel15b
is shown in Fig. 11.
|
[Click on top of figure to display] |
Fig. 11 Output from
onlinechannel15b for Example No. 1.
|
The results are: Q = 50 m3/s;
v = 8.088 m/s;
F = 2.501;
β = 1.607;
Fns = 1.646; and
V = 1.519.
Since V > 1, it is concluded that this flow condition may lead to flow instability.
Note that for this rectangular cross section,
β = 1.607 is
near the top of the feasible range (1 ≤ β ≤ 5/3).
In Example No. 2, assume b = 1.2 m,
y = 2.391 m,
z1 = 0.5,
z2 = 0.5,
n = 0.025, and
S = 0.057. The output from onlinechannel15b
is shown in Fig. 12.
|
[Click on top of figure to display] |
Fig. 12 Output from onlinechannel15b for Example No. 2.
|
The results are: Q = 50.03 m3/s;
v = 8.735 m/s;
F = 2.208;
β = 1.4;
Fns = 2.497, and
V = 0.884.
Since V < 1,
it is concluded that this flow condition will not lead to flow instability.
In this case, the cross section is trapezoidal, and β = 1.4 is
close to a central value within the feasible range (1 ≤ β ≤ 5/3).
We note that the choice of cross-sectional shape and channel
dimensions with the objective of
reducing β
must be done judiciously. For example, a wide trapezoidal channel may not necessarily
lead to a reduction in the value of β, because the increase in top width
T
will result in a decrease in hydraulic depth D, leading to
an increase in the Froude and Vedernikov numbers.
9. THE NATURE OF β
The value of β is smaller not only for triangular
channels, but also for narrow channels. Table 3 show calculations of
β for six different test channels
(See box below) to pass a reference discharge Q =
50 m3/s. To emulate the La Paz case study,
we have assumed for these test channels a Manning's n = 0.025 and
channel slope S = 0.057 (See Section 11).
Test channels:
A rectangular channel.
A trapezoidal channel.
A triangular channel with the same side slopes (z1 = 1 and z2 = 1).
A triangular channel with different side slopes
(z1 = 0.5 and z2 = 1).
A narrow and deep rectangular channel.
A very narrow rectangular channel to pass Q /10
(the diffuser concept, see Section 10).
|
|
Table 3 Calculations of β and V for
selected channel shapes (n = 0.025 and S = 0.056).
|
| i |
Shape |
b |
y |
z1 |
z2 |
|
Q |
v |
F |
β |
Fns |
V |
| 1 |
Rectangular |
5.8 |
1.066 |
0 |
0 |
|
50.00 |
8.088 |
2.501 |
1.607 |
1.646 |
1.519 |
| 2 |
Trapezoidal |
1.2 |
2.391 |
0.5 |
0.5 |
|
50.03 |
8.735 |
2.208 |
1.4 |
2.497 |
0.884 |
| 3 |
Triangular
(z1 = z2) |
0 |
2.413 |
1 |
1 |
|
50.01 |
8.590 |
2.497 |
1.333 |
2.999 |
0.832 |
| 4 |
Triangular
(z1 ≠ z2) |
0 |
2.810 |
1 |
0.5 |
|
50.03 |
8.449 |
2.276 |
1.333 |
2.999 |
0.758 |
| 5 |
Narrow and deep |
1.8 |
3.619 |
0 |
0 |
|
50.00 |
7.676 |
1.288 |
1.366 |
2.728 |
0.472 |
| 6 |
Very narrow
(for Q /10) |
0.5 |
2.795 |
0 |
0 |
|
5.002 |
3.579 |
0.683 |
1.231 |
4.328 |
0.157 |
The following conclusiones are drawn from Table 3:
Conclusions:
β is quite large (β = 1.607) for the rectangular channel (i = 1).
β decreases somewhat (to β = 1.4) for the trapezoidal channel (i = 2).
β decreases to 1.333 for the triangular channel with equal side slopes (i = 3).
β decreases to 1.333 for the triangular channel with different side slopes (i = 4).
β decreases substantially (to β = 1.356) for the narrow and deep channel (i = 5).
β decreases substantially (to β = 1.231) for the very narrow channel (for Q /10) (i = 6).
|
For the given test cases, Table 3 shows that as β decreases, V also decreases. In particular, for test cases 2 to 6,
the Vedernikov number remains V < 1, assuring flow stability
and the consequent absence of roll waves. Moreover, for the very narrow section (i = 6),
β reduces further to β = 1.269, with
a corresponding V = 0.181, the latter seen to be
a definitely low value.
We conclude that β is of paramount importance in the hydraulic design of open channels to avoid flow instability and associated roll waves.
10. MECHANICAL CONTROL OF ROLL WAVES
The Vedernikov criterion is seen to be a necessary condition,
but it may be not sufficient for the occurrence of roll waves (See
Section 5). Since there is a preferential scale of dimensionless wavenumbers for roll-wave
propagation (Fig. 8), whether a roll-wave event will occur may also depend on the
upstream boundary condition, i.e., on the (dimensionless) scale of the incoming wave.
Therefore, there is a randomness or stochasticity about the occurrence of a roll-wave event, which precludes it from
happening too frequently or, otherwise, at regularly timed intervals.
In addition to the effective
assessment of the value of the Vedernikov number, roll-wave events may also be controlled
by mechanically attenuating (i.e., diffusing) the preferential wavenumbers if, by chance, they happen to be present.
This can be accomplished by placing a momentum diffuser in the flow, at or near the upstream
boundary. A momentum diffuser separates the flow into a series of narrow channels (Fig. 13). The additional boundary friction, coupled with
the small aspect ratio (B /y) of the diffuser channel elements, cause the value of β to drop (Fig. 14).
This fact is confirmed by the data of Table 3, line 6, for which β = 1.231 and
V = 0.157.
Fig. 13 Schematic diagram of a typical cross section of a momentum diffuser.
|
Fig. 14 A narrow flood channel draining into Laguna del Carpintero,
in Tampico, Tamaulipas, Mexico.
|
In practice, a properly designed momentum diffuser
will most likely require physical and/or
mathematical modeling to adequately
determine its hydraulic properties and size its geometric features.
11. CASE STUDY: LA PAZ RIVER TRIBUTARIES, BOLIVIA
The findings of this article are complemented with a case study of two tributaries of the
La Paz river,
which flow across the city of
Nuestra Señora de La Paz,
commonly referred to simply as La Paz, in the department of
the same name, Bolivia. The department of La Paz is shown in wine color, immediately east of Peru
on the map to the right (Fig. 15).
Note the approximate location of the watershed as the small blue dot inside
the department (click here ⇒ Fig. 15 to display the map).
|
[Click on top of figure to display] |
Fig. 15 Watershed of the La Paz river, department of La Paz, Bolivia.
|
The watershed of the La Paz river comprises 496.4 km2 and features six (6)
tributaries:
(1) Choqueyapu, (2) Orkhojahuira, (3) Irpavi,
(4) Achumani, (5) Jillusaya, and (6) Huayñajahuira (Fig. 15).
In the rainy season 2018-19, comprising the period
from October 2018 to April 2019, several roll-wave events have been documented in the Achumani and
Huayñajahuira rivers. The details are shown in Table 4.
|
Table 4
Roll-wave events documented in La Paz river tributaries in the period October 2018 - April 2019. |
Tributary
stream
| ID
| Station
| No.1
| b
(m)
| y
(m)
| S
(m/m)
| Local S (m/m)
| Drops
| Description
|
Achumani
River(Drainage area:
50.39 km2)
| 1
| ACHHIC008
| 2
| 11.68
| 1.53
| 0.059
| 0.002
| Yes
| Zona Huayllani Humapalca
|
| 2
| ACHHIC003
| 1
| 14.90
| 1.73
| 0.059
| 0.034
| No
| Asilo San Ramón -
Av. The Strongest
|
| 3
| ACHHIC002
| 1
| 14.85
| 2.08
| 0.059
| 0.034
| No
| Achumani Puente Koani
|
| 4
| ACHHIC001
| 1
| 15.71
| 2.18
| 0.059
| 0.048
| No
| Av. General Inofuentes, altura Calle 12 de Calacoto
|
|
Huayñajahuira
River(Drainage area:
18.44 km2)
| 5
| Calle 8 Calacoto
| 1
| 10.32
| 4.60
| 0.057
| 0.016
| Yes
| Av. Los Alamos, entre Av. Arequipa y Calle 12 de Calacoto
|
| 6
| HUAHIC_AF
| 2
| 5.80
| 3.71
| 0.057
| 0.016
| Yes
| Av. Circumvalación Alto Florida, Zona Alto La Florida
|
| 7
| Calle 16 Calacoto
| 2
| 5.54
| 2.44
| 0.057
| 0.017
| Yes
| Av. Monseñor José Quiróz, entre Calles 15 y 16 de Calacoto
|
| 8
| HUAHI002
| 2
| 5.80
| 3.62
| 0.057
| 0.036
| Yes
| Av. Costanera, Esq. Pablo Guillén
|
| 9
| Puente La Razón
| 2
| 5.71
| 2.59
| 0.057
| 0.034
| Yes
| Av. Los Jazmines, entre Calles 2 y 3
|
| 10
| Puente Calle 25
| 2
| 5.69
| 2.08
| 0.057
| 0.048
| Yes
| Av. Costanera, casi Puente Calle 25, Zona Cota Cota
|
| 11
| HUAHI003
| 2
| 5.80
| 2.18
| 0.057
| 0.052
| Yes
| Calle 35 de Cota Cota, Calle Jacaranda
|
| 12
| HUAHI004
| 2
| N.A.
| N.A.
| 0.057
| N.A.
| N.A.
| Av. Panamericana, Esq. Calle 53, altura Puente Bayler
|
| 1 Number of events documented in the indicated period. |
The channels are built using stone-masonry walls and unlined channel beds; see Figs. 16 and 17.
Most channel reaches have instream vertical drops
for slope reduction and grade control (Table 4). An approximate value
of wave celerity c = 10.5 m/s
has been obtained from available videos of roll-wave events.
Therefore, assuming a value of β ≈ 1.5,
the mean velocity of the flow (now referred to as v) may be approximated as follows: v = c / β = 7 m/s.
Fig. 16 The Achumani river.
|
Fig. 17 The Huayñajahuira river.
|
Pending additional studies,
the Manning friction coefficient
has been estimated at n = 0.030 for the Achumani river (Fig. 16)
and n = 0.025 for the Huayñajahuira river (Fig. 17)
(Chow, 1959).
Table 5 shows calculations of β and V for
seven (7) selected channel reaches
(stations) with relatively steep local slopes (Slocal ≥ 0.034; Table 4).
In order to compare events of similar frequency, the flow depths were set to
pass the same discharge, chosen as Q25 = 106.1 m3/s for the Achumani river and
Q25 = 30.97 m3/s for the Huayñajahuira river
(Plan Maestro de Drenaje, 2007).
The calculated mean flow velocities shown in Table 5 are confirmed to be
around v = 7 m/s, a clear indication that channel friction
has been properly estimated.
It is seen
that all the channel reaches under consideration
have Vedernikov numbers V > 1, confirming the hydraulic
conditions under which roll waves are likely to occur.
In addition, it is shown that all reaches have β > 1.6, i.e., clearly near the top of the feasible range
(1 ≤ β ≤ 1.67).
The existence of channel drops adds a bit of complexity to the analysis,
since the flow could no longer
be considered to be strictly one-dimensional.
Therefore, the present analysis is only an approximation,
subject to detailed field verification when appropriate.
|
Table 5
Selected roll waves documented in La Paz river tributaries in the period October 2018 - April 2019. |
Tributary
stream
| ID
| Station
| Q
(m3/s)
| v
(m/s)
| F
| β
| Fns
| V
| Description
|
Achumani
River(Drainage area:
50.39 km2)
| 2
| ACHHIC003
| 106.2
| 7.325
| 2.371
| 1.643
| 1.553
| 1.526
| Asilo San Ramón -
Av. The Strongest
|
| 3
| ACHHIC002
| 106.1
| 7.332
| 2.371
| 1.643
| 1.553
| 1.526
| Achumani Puente Koani
|
| 4
| ACHHIC001
| 106.2
| 7.200
| 2.373
| 1.645
| 1.549
| 1.531
| Av. General Inofuentes, altura Calle 12 de Calacoto
|
|
Huayñajahuira
River(Drainage area:
18.44 km2)
| 8
| HUAHI002
| 30.98
| 6.885
| 2.495
| 1.621
| 1.607
| 1.552
| Av. Costanera, Esq. Pablo Guillén
|
| 9
| Puente La Razón
| 30.98
| 6.911
| 2.491
| 1.620
| 1.610
| 1.546
| Av. Los Jazmines, entre Calles 2 y 3
|
| 10
| Puente Calle 25
| 30.97
| 6.917
| 2.490
| 1.620
| 1.611
| 1.545
| Av. Costanera, casi Puente Calle 25, Zona Cota Cota
|
| 11
| HUAHI003
| 30.98
| 6.885
| 2.495
| 1.621
| 1.607
| 1.552
| Calle 35 de Cota Cota, Calle Jacaranda
|
12. CONCLUSIONS
The theoretical foundations and relevant experience with open-channel flow instability
are
examined with the objective of controlling roll waves.
The latter seem to recur with relative frequency in channelized rivers where the Vedernikov number has
increased, due to the channelization, above the threshold V = 1
(click on Fig. 18 at the end of this article to watch a video of a pulsating wave event).
Channelization with rectangular
cross sections typically increases the value of β,
the exponent of the discharge-flow area rating, triggering an increase in the Vedernikov number
above
the threshold of flow instability (V = 1).
It is shown that the choice of β (at the design stage) is of paramount importance in the control
of roll waves.
Several examples show conclusively the existence of a definite relation between β and V, namely,
that as the cross-sectional shape departs from rectangular towards triangular,
β
decreases accordingly, lowering the value of V.
A sufficient decrease in β will
cause V to drop below the threshold of instability.
Shallow wave propagation theory reveals the existence of a preferential scale for the amplification of surface perturbations in the
unstable regime
(V ≥ 1) (Fig. 8). Therefore, the Vedernikov criterion may not be sufficient
to produce roll waves in all cases.
The latter may depend on conditions at the upstream boundary, which are likely to be
of a stochastic nature.
The provision of a momentum diffuser is introduced; the diffuser is designed
to attenuate roll waves at the point where they may originate, i.e.,
at or near the entrance to the
channelized stream. Further analysis and testing is recommended to carry the diffuser concept to development stage.
The methodology developed herein is applied to two channelized rivers in La Paz, Bolivia,
where large roll waves (pulsating waves) have been shown to recur with
increasing frequency. The analysis confirms
that where roll waves have occurred in these channelized rivers,
they have done so under β > 1.6 and V > 1.
The results
underscore the promise of β
analysis in the hydraulic design of channelized rivers with the objective of controlling roll waves.
ACKNOWLEDGMENTS / AUTHORS
|
| |
This study is a contribution toward the solution of the roll-wave (or pulsating wave)
problem in La Paz, Bolivia. The field data was provided by
the Secretaría
Municipal de Gestión Integral de Riesgos SMGIR
(Municipal Secretariat
for the Integral Management of Risks) of the city of La Paz. | |
Victor Miguel Ponce is professor of civil engineering at San Diego State University, California.
Beatriz Choque Guzmán is a staff hydraulic engineer with SMGIR.
Thanks are due to Mariel Rivera, civil engineer, for her continued support and encouragement.
| |
REFERENCES
Brock, R. R. (1967). Development of roll waves in open channels. Report No. KH. R-16,
W. M. Keck Laboratory of Hydraulics and Water Resources, California institute of Technology, Pasadena. Calif.
Chow, V. T. 1959. Open-channel Hydraulics. Mc-Graw Hill, New York.
Cornish, V. 1907. Progressive waves in rivers. Journal of the Royal Geographical Society, Vol. 29, No. 1, January, 23-31.
Craya, A. 1945. Calcul graphique des régimes variables dans lex canaux. La Hoiulle Blanche, No. 1, 39-60.
Craya, A. 1952.
The criterion for the possibility of roll wave formation. Gravity Waves, Circular 521, 141-151,
National Institute of Standards and Technology, Gaithersburg, MD.
Lagrange, J. L. de. 1788. Mécanique analytique. Paris, part 2, section II, article 2, p 192.
Liggett, J. A. (1975). Stability, in Unsteady flow in open channels,
Vol. 1, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Fort Collins, Colo., 259-281.
Lighthill, M. J., and G. B. Whitham. 1955.
On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
Plan Maestro de Drenaje. 2007. Revisión y Actualización del Plan Maestro de Drenaje para la Ciudad de La Paz. Informe Final,
Gobierno Municipal de La Paz (GMLP), República de Bolivia,
Octubre.
Ponce, V, M., and D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V, M., and M. P. Maisner. 1993.
Verification of theory of roll wave formation. Journal of Hydraulic Engineering, ASCE, Vol. 119, No. 6, June, 768-773.
Ponce, V. M., and P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April,
376-380.
Ponce, V. M. 2002. That's the one we skip! Legacy Tale. ponce.sdsu.edu
Ponce, V. M. 2014. Fundamentals of open-channel hydraulics. Online textbook.
Ponce, V. M. 2014. Chow,
Froude and Vedernikov. Online paper.
Ponce, V. M. and M. Diaz. 2016. The inherently stable channel with online computation. Online paper.
Powell, R. W. 1948.
Vedernikov's criterion for ultra-rapid flow.
Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.
Seddon, J. A. 1900. River hydraulics.
Transactions, ASCE,
Vol. XLIII, 179-243, June.
Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid. Doklady Akademii Nauk USSR, 48(4), 239-242.
Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel. Doklady Akademmi Nauk USSR, 52(3), 207-210.
|
[Click on top of photo to watch video] |
Fig. 18 Roll-wave event recorded in the Huayñajahuira river, on April 30, 2019.
|
|