[Place mouse over picture to show Vedernikov]
froude
[Place mouse out to recover Froude]

FROUDE AND VEDERNIKOV:  PILLARS

OF OPEN-CHANNEL HYDRAULICS


Victor M. Ponce

Professor Emeritus of Civil and Environmental Engineering

San Diego State University, San Diego, California


May 23, 2024

ABSTRACT.  We have shown that there are only three velocities that characterize open-channel flow across a wide variety of applications in steady and unsteady flow, including channel design, flow control, flood routing, and surface-flow instability. These are: (1) mean flow velocity u, (2) relative celerity of kinematic waves v, and (3) relative celerity of dynamic waves w. These three velocities give rise to only two independent dimensionless numbers: (1) Froude number F = u/w, and (2) Vedernikov number V = v/w. The third ratio, v/u, properly V/F, is equal to (β - 1), wherein β is the exponent of the discharge-flow area rating (Q = αAβ). Thus, β encapsulates both the Froude and Vedernikov numbers, while describing the frictional and cross-sectional properties of the channel under consideration. Indeed, the Froude and Vedernikov numbers constitute the two pillars on which the entire field of open-channel hydraulics rests.

1.  INTRODUCTION

Around the beginning of the twentieth century, hydraulic engineering, a branch of civil engineering, began to experience an accelerated pace of development. The world's population was increasing, and it was becoming patently clear that human societies had to rely on the hitherto novel scientific method for the utilization and management of water resources. Well in the twentieth century, the use of the Froude number, developed in England in the 1860s, became established in hydraulic engineering practice.

The Froude number defined the threshold wherein the mean flow velocity in an open channel is equal to the relative velocity, i.e., the relative celerity, of a small surface disturbance. Several decades later, specifically in the middle of the twentieth century (1945-46), the concept of Vedernikov number arose in the former Soviet Union. The latter compared the celerity of a small disturbance, driven by energy gradients, to that of a large disturbance, driven by mass gradients.

In this article, we will show that the three velocities defining the two concepts of Froude and Vedernikov are the only velocities which may be readily identified in the field of open-channel hydraulics. This fact surely makes these two fundamental concepts the two pillars on which the entire field of open-channel hydraulics rests. The historical flavor with which we endeavor to present the topic significantly enhances the theory and goes the extra mile to clarify the technical concepts. We surmise that the profession should be altogether better because of it.

2.  WILLIAM FROUDE:  A SHORT BIO

William Froude was a distinguished British engineer, hydrodynamicist and naval architect. Born in Dartington, Devon, England on November 28, 1810, he died from a stroke at age 69 on a cruise to Simon's Town, South Africa.

He acquired his education in mathematics at Oxford. In 1832, immediately after his graduation, he worked for Isambard Kingdom Brunel, the famed developer of railways, as a surveyor on the Great Western Railway, in England. In 1857, Brunel consulted him on the behavior of the Great Eastern ship at sea; based on Froude's recommendations, Brunel modified the design of the ship to avoid rolling.

Starting in 1859, Froude built the first towing tank, using his own resources. He carried out ship model experiments using the tank, first at his home in Paignton, Devon County, and later, in his other home, called Chelston Cross, in Torquay.

In 1861, he wrote a paper on the design of ship stability, published in the Proceedings of the Institution of Naval Architects. Between 1863 and 1867, he showed the relation between model and prototype, stating that the frictional resistance was equal in both when the speed V was proportional to the square root of the length L. He called this concept the Law of Comparison:

V  =  k  L1/2
(1)

wherein k is a constant that applies to both model and prototype. Equation 1 is known as Froude's law.

Froude was the first to identify the most efficient shape for the hull of ships, as well as to predict ship stability based on reduced-scale models (Fig. 1). In open-channel hydraulics, Froude's law is embodied in the Froude number, defined as follows:

F = V / (gD) 1/2

(2)

in which V = mean flow velocity, D = hydraulic depth, and g = gravitational acceleration. Ostensibly, the denominator of Eq. 2 is the relative celerity of dynamic waves (Ponce, 2023a).

Unlike k in Froude's law (Eq. 1), the Froude number F in Eq. 2 is dimensionless. In open-channel hydraulics, the ship length L (a horizontal measure) has been replaced by the hydraulic depth D (a vertical measure) to properly account for the gravitational force.

William M Connolley (Wikipedia)
Fig. 1  The hulls of Swan (above) and Raven (below) on display at the Science Museum, London.
The models were built by Froude to establish resistance and scaling laws for ship design.

3.  VALENTIN V. VEDERNIKOV:  A SHORT BIO

Valentin Valentinovich Vedernikov, doctor of technical science (Russian/Soviet terminology; a step above PhD in the Western world), graduated from Don's Polytechnical Institute (City of Novocherkassk, Rostov Oblast Region) in 1928. He worked at the State Institute of Agricultural Land Reclamation, as well as in various water management organizations of the Northern Caucasus Region and Turkestan, presently in Middle Asia.

In 1934, Vedernikov published a book entitled Seepage from channels, in which he used a method of conformal images for non-pressurized steady motion of ground water in a vertical plane. In this book he used, for the first time, the method of Vedernikov-Pavlovskiy. The latter is based on conformal imaging of flow regions in the plane of complex potential of velocity of seepage and the Zhukovkiy complex function.

In 1935, Vedernikov was granted the Ph.D. without defending his dissertation; in 1938 he defended his dissertation and received the degree of Doctor of Technical Sciences. The findings of V. V. Vedernikov were summarized in the book entitled Theory of seepage and its use in the fields of irrigation and drainage, published in 1939.

In 1940-1941, Vedernikov was chair of the Department of Hydraulics and Hydromachinery at the Moscow Institute of Turf. In 1941-1942 he was working in the Institute of Mechanics of the USSR Academy of Sciences. Beginning in 1943, he worked at the Section of Scientific Research in Hydraulics of the Soviet Academy of Sciences. In 1947 he became chair of the Department of Hydraulics of the Soviet Union's Energy Distance-Learning Institute.

In 1945-1947, Vedernikov, theoretically, and later experimentally, explained the phenomenon of unsteady flow of water in channels with roll wave formation, defining the criterion for the instability of flow (Fig. 2). To accomplish this task, he used the Saint-Venant equations of unsteady open-channel flow. In the literature of hydraulic engineering, his concept is referred to as the Vedernikov number (Powell, 1948; Chow, 1959). His research helped to advance the knowledge of the theory of seepage, as well as the design and construction of hydraulic and irrigation/drainage structures.

Cornish (1907)

Fig. 2  Early fotograph of a train of roll waves in the Swiss Alps.

This short biography of Prof. V. V. Vedernikov was prepared using original sources by Aleksandr Gostomelskiy at the request of Prof. Victor M. Ponce. The assistance of Prof. Dmitriy Vyacheslavovich Kozlov, chair of the Department of Hydraulics and Hydraulic Construction at Moscow State University of Construction, is gratefully acknowledged. The photo of Prof. Vedernikov was provided by Prof. Kozlov (2021).

4.  VELOCITIES IN OPEN-CHANNEL FLOW

Steady flow:  Mean velocity

There are three distinctive velocities in open-channel flow (Ponce, 1991). The first is the mean velocity of the steady flow, herein referred to as u. This velocity is calculated using the Chezy or Manning equations (Ponce, 2014: Chapter 5). The Chezy formula is the following (Chezy, 1776):

u = C (RS) 1/2

(3)

in which u = mean velocity of the steady uniform (equilibrium) flow, with units of L/T (m/s or fps); C = Chezy coefficient, with units L1/2T -1 (m1/2/s, or ft1/2/s); R = hydraulic radius, with units of L (m, or ft); and S = channel slope, or bottom slope, which is the same as friction slope in steady uniform flow, in dimensionless units (m/m, or ft/ft).

The Manning formula in the SI system of units is the following (Manning, 1889):

u = (1/n) (R) 2/3 S1/2

(4)

in which u = mean velocity of the steady uniform flow, in m/s; n = Manning coefficient; and R (in m) and S (in m/m) have been defined previously. The corresponding Manning formula in U.S. Costumary units is:

u = (1.486/n) (R) 2/3 S1/2

(5)

in which R (in ft) and S (in ft/ft).

While the Manning equation is usually preferred in engineering practice, the Chezy equation may be readily expressed in dimensionless form, clearly a definite advantage, particularly for theoretical studies (Ponce, 2014: Chapter 5).

The mean flow velocity u is calculated using either of the well-known Manning or Chezy formulas of open-channel hydraulics.

Equations 3 to 5 calculate the mean flow velocity u, i.e., the velocity of steady uniform, or equilibrium, flow. The remainder of this section will describe the two other velocities relevant in open-channel flow, i.e., the velocities, or more properly, celerities, that characterize unsteady flow.

Unsteady flow:  Two wave celerities

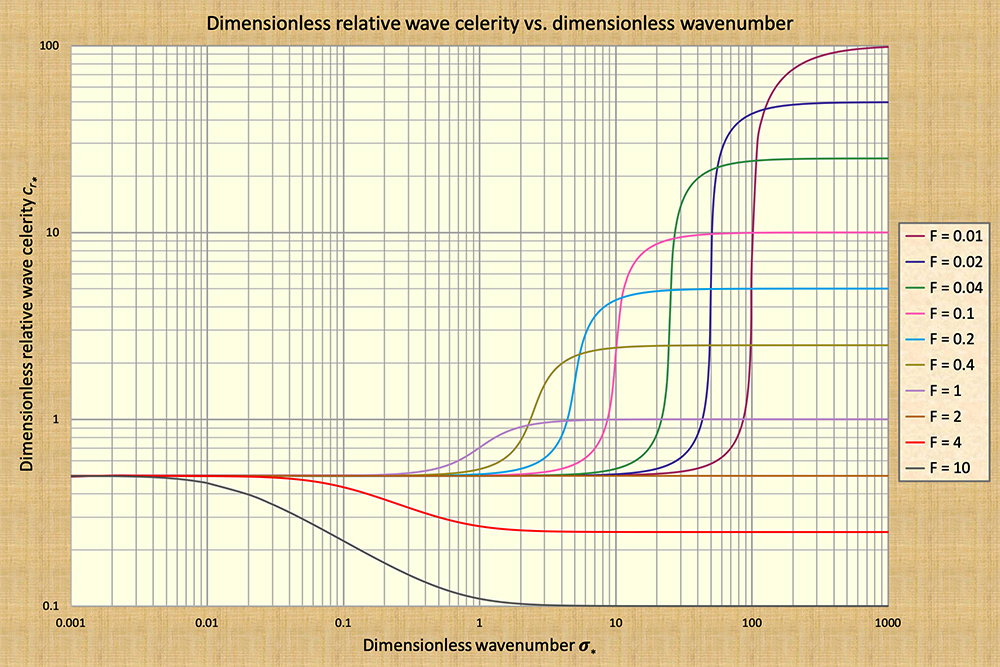
There are two wave celerities which complete the triad of velocity/celerities in open-channel flow: (1) kinematic wave celerity; and (2) dynamic wave celerity. A kinematic wave is a "large" surface disturbance, i.e., a wave featuring a small dimensionless wavenumber, in the sense of Ponce and Simons (1977). Conversely, a dynamic wave is a "small" surface disturbance, a wave featuring a large dimensionless wavenumber.

The difference between kinematic and dynamic waves is admirably depicted in the plot of dimensionless relative wave celerities vs. dimensionless wavenumbers (Fig. 3). Kinematic waves plot to the left, while dynamic waves plot to the right. From a historical perspective, kinematic waves are those of Seddon (1900); dynamic waves are those of Lagrange (1788). Wave attenuation for either kinematic or dynamic waves is too small or nonexistent, because the dimensionless relative wave celerities (in the ordinates) in both extremes of the spectrum (left and right) remain constant and independent of dimensionless wave number (in the abscissas).

Ponce and Simons (1977)

Fig. 3  Dimensionless relative wave celerity vs. dimensionless wavenumbers in shallow wave propagation in open-channel flow.

The kinematic wave celerity is: ck = β u, in which β is the exponent of the discharge-flow area rating Q = αAβ (Ponce, 2014: Chapter 10). Therefore, the relative kinematic wave celerity (i.e., the celerity relative to the mean flow velocity) is: crk = v = β u - u = (β - 1) u. The dimensionless relative kinematic wave celerity is: cdrk = crk /u = v /u = β - 1. The value of β is a function of type of friction and cross-sectional shape (Ponce, 2014: Chapter 1). For the case of Chezy friction in a hydraulically wide channel: β = 1.5. Therefore, cdrk = 0.5. This value is plotted in Fig. 3 on the left margin.

The dimensionless relative kinematic wave celerity v is obtained by subtracting the mean flow velocity from the kinematic wave celerity and dividing the result by the mean flow velocity.
This operation leads to: v = β - 1.

The dynamic wave celerity has two components: cd = u ± (gD)1/2, in which g = gravitational acceleration, D = hydraulic depth = A /T (Ponce, 2014: Chapter 1). Therefore, the relative dynamic wave celerity (i.e., the celerity relative to the mean flow velocity) is: crd = w = (gD)1/2. The dimensionless relative dynamic wave celerity is: cdrd = crd /u = w /u = 1/F, in which F = Froude number. Figure 3 shows, toward the right margin, the plotting of several values of cdrd, corresponding to their respective Froude numbers; for instance, for F = 0.01: w = 100; for F = 0.1: w = 10; and for F = 1: w = 1.

The dimensionless relative dynamic wave celerity w is obtained by subtracting the mean flow velocity from the dynamic wave celerity and dividing the result by the mean flow velocity. The resulting value of w is the reciprocal of the Froude number: w = 1/F.

In summary, the three velocities (one velocity and two celerities) preeminent in open-channel flow, including both steady and unsteady flow, are: (1) u = mean flow velocity, (2) v = relative kinematic wave celerity, and (3) w = relative dynamic wave celerity, wherein all three values are properly defined in terms of hydraulic variables (Table 1).

Table 1.  Celerities in open-channel flow.
Type of celerity Total celerity Relative celerity Dimensionless relative celerity
Kinematic ck = β u v = crk = β u - u = (β - 1) u cdrk = β - 1
Dynamic cd = u ± (gD)1/2 w = crd = (gD)1/2 cdrd = (gD)1/2/u = 1/F

We will show here that these three velocities/celerities (u, v, and w) may produce only two independent dimensionless numbers: (1) the Froude number, and (2) the Vedernikov number. In fact, the third "ratio" amounts to the ratio of Vedernikov and Froude numbers, properly: V/F = β - 1. Thus, we confirm that the exponent β (of the rating Q vs. A) is the all-important parameter in open-channel hydraulics, encapsulating both the Froude and Vedernikov numbers.

5.  THE FROUDE NUMBER

The Froude number is defined as the ratio of the mean flow velocity u to the relative celerity of dynamic waves w (Ponce, 1991):

F = u /w

(6)

In other words, the Froude number compares the mean velocity of the flow to the relative celerity (speed) of small (dynamic) surface perturbations. Three situations are possible:

  • For w > u, then F < 1, and the flow is in a subcritical state. Since w > u, the result of (u - w) < 0, and the perturbation is able to travel upstream; consequently, the flow may be controlled only from a downstream location.

  • For w = u, then F = 1, and the flow is in a critical state. Since w = u, the result of (u - w) = 0, and the perturbation remains stationary; it is not able to travel either upstream or downstream. In practice, a state of critical flow is unusual; its presence is revealed by the appearance of small surface disturbances, often with a marked tendency to persist (Fig. 4).

  • For w < u, then F > 1, and the flow is in a supercritical state. Since w < u, the result of (u - w) is > 0, and the perturbation is unable to travel upstream; consequently, the flow may be controlled only from a upstream location.

The above statements are summarized in Table 2.

Table 2.  States of flow characterized by the Froude number (F = u /w).
State
of flow 		Velocity relation Froude number Direction of travel of secondary disturbances Location of
flow control
Subcritical w > u F < 1 Upstream Downstream
Critical w = u F = 1 Stationary Undefined
Supercritical w < u F > 1 Downstream Upstream

Fig. 4  Tinajones Feeder Canal, operating close to critical state, near Chiclayo, Lambayeque, Peru.

6.  THE VEDERNIKOV NUMBER

The Vedernikov number is defined as the ratio of the relative celerity of kinematic waves v to the relative celerity of dynamic waves w (Ponce, 1991):

V = v /w

(7)

In other words, the Vedernikov number compares the relative celerity of "large" (of small dimensionless wavenumber) kinematic waves, i.e., those driven by mass gradients, to the relative celerity of "small" (of large dimensionless wavenumber) dynamic waves, i.e., those driven by energy gradients (Ponce and Simons, 1977; Ponce, 2023b). Three situations are possible:

  • For w > v, then V < 1, and the flow is in stable state. Since w > v, it follows that (w - v) > 0; consequently, the primary energy disturbance, traveling downstream (with relative dynamic wave celerity w) travels faster than the mass disturbance (with relative kinematic wave celerity v). Therefore, the energy wave runs ahead of the mass wave, and the flow remains stable, with roll waves conspicuously absent.

  • For w = v, then V = 1, and the flow is in neutrally stable state. Since w = v, it follows that (w - v) = 0; consequently, the primary energy disturbance, traveling downstream (with relative dynamic wave celerity w), travels at the same speed as the mass disturbance (with relative kinematic wave celerity v). Therefore, the mass wave rides the energy wave, and the flow becomes neutrally stable, at the threshold of roll wave formation.

  • For w < v, then V > 1, and the flow is in unstable state. Since w < v, it follows that (w - v) < 0; consequently, the primary energy disturbance, traveling downstream (with relative dynamic wave celerity w), travels slower than the mass disturbance (with relative kinematic wave celerity v). Therefore, the mass wave overcomes the energy wave, and the flow becomes unstable, with the manifested presence of roll waves (Fig. 5).

    The above statements are summarized in Table 3.

    Table 3.  States of flow characterized by the Vedernikov number (V = v /w).
    State
    of flow     		Velocity relation Vedernikov number Leading wave type
    Stable w > v V < 1 Energy, dynamic (w)
    Neutrally stable w = v V = 1 At threshold (energy → mass)
    Unstable w < v V > 1 Mass, kinematic (v)

    Fig. 5  Roll waves traveling in a steep irrigation canal, Cabana-Mañazo, Puno, Peru.

7.  THE EXPONENT OF THE RATING

The third relation of a total of three  [besides (1) F = u /w, and (2) V = v /w]  is: (3) v /u; effectively, the third relation is: v /u = V/F.

V/F = v /u

(8)

Note that the kinematic wave celerity (Section 4) is: ck = βu, in which β is the exponent of the discharge-flow area rating Q = αAβ. Therefore, the relative kinematic wave celerity (relative to the flow) is: crk = β u - u = (β - 1) u. The dimensionless relative kinematic wave celerity is: cdrk = crk /u = β - 1. It follows that the third relation amounts to, and is expressed solely in terms of, the exponent of the rating:

V/F = β - 1

(9)

In other words, the exponent β of the rating (Q = αAβ) encapsulates the Froude and Vedernikov numbers, such that β = (V/F) + 1. Furthermore, for V = 1, i.e., for neutrally stable flow, the neutrally stable Froude number is: Fns = 1 / (β - 1). For instance, for β = 1.5, i.e., for Chezy friction in a hydraulically wide channel: Fns = 2. This finding is confirmed by Fig. 3, wherein the full horizontal line, applicable for F = 2, remains constant for all wave sizes, kinematic and dynamic, and neither attenuates nor amplifies (F = 2 corresponds to the neutrally stable state, applicable for Chezy friction in hydraulically wide channels).

Table 4 shows the variation of the neutrally stable Froude number Fns with the exponent β (Ponce, 2023b). This table shows that the neutrally stable Froude number Fns increases from hydraulically wide to triangular cross-sectional shape. In other words, as the channel cross-section changes from hydraulically wide (near trapezoidal) to triangular, the onset of flow instability (the roll waves) occurs at a higher Froude number, thus, enhancing flow stability. We conclude that the cross-sectional shape, as described by β, is the overriding factor in assessing and controlling flow instability (Fig. 6) (Ponce and Choque, 2019).

Table 4.  Variation of Fns with β with type of friction and cross-sectional shape.
Type of friction Cross-sectional shape β β - 1 Fns
Laminar Hydraulically wide 3 2 0.5
Turbulent Manning Hydraulically wide 5/3 2/3 3/2
Turbulent Chezy (refer to Fig. 3) Hydraulically wide 3/2 1/2 2
Turbulent Manning Triangular 4/3 1/3 3
Turbulent Chezy Triangular 5/2 1/4 4

The above conclusions merit the elevation of the exponent of the rating β to a singular and privileged position in the field of open-channel hydraulics. The exponent β contains both Froude and Vedernikov numbers exclusively, while going the extra mile to describe both friction and cross-sectional properties (Table 3). We reckon that the Vedernikov number varying with friction and cross-sectional shape is the original finding of Vedernikov (1945, 1946), although he did not quite present it in a similar way [Chow (1959): Extract: Page 210].

The exponent of the rating β is regarded as the most important concept in open-channel hydraulics. While it is singularly defined in terms only of the Froude and Vedernikov numbers, the only dimensionless numbers of wide applicability, it also describes the friction and cross-sectional shape, two very significant components of open-channel hydraulics.

Courtesy of Jorge Molina Carpio

Fig. 6  Roll waves, also referred to as pulsating waves, overtopping the Huayñajahuira river channel, in La Paz, Bolivia, on December 11, 2021.

8.  CONCLUDING REMARKS

We have shown that there are only three velocities (properly, one velocity and two celerities) that generally characterize open-channel flow across a wide variety of applications in steady and unsteady flow, including channel design, flow control, flood routing, and surface-flow instability. These are: (1) mean flow velocity u, (2) relative celerity of kinematic waves v, and (3) relative celerity of dynamic waves w.

These three velocities give rise to only two independent dimensionless numbers: (1) Froude number F = u/w, and (2) Vedernikov number V = v/w. The third ratio, v/u, properly V/F, is equal to (β - 1), wherein β is the exponent of the discharge-flow area rating (Q = αAβ). Thus, β is shown to encapsulate both the Froude and Vedernikov numbers, while describing the frictional and cross-sectional properties of the channel under consideration. Indeed, the Froude and Vedernikov numbers constitute the two pillars on which the entire field of open-channel hydraulics rests.

REFERENCES

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.  Extract: Page 210.

Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, 192.

Ponce, V. M. and D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476.

Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, 27(7), 1777-1779.

Ponce, V. M. 2014. Fundamentals of Open-channel Hydraulics. Online textbook.

Ponce, V. M. and B. Choque Guzman. 2019. The control of roll waves in channelized rivers. Online article.

Ponce, V. M. 2023a. The states of flow. Online article.

Ponce, V. M. 2023b. Ths Vedernikov number. Online article.

Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, 29(6), 882-886.

Seddon, J. A. 1900. River Hydraulics. Transactions, American Society of Civil Engineers, XLIII(179-243), June; Extract: pages 218-223.

Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid. Doklady Akademii Nauk USSR, 48(4), 239-242.

Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel. Doklady Akademmi Nauk USSR, 52(3), 207-210.

240528