THE STATES OF FLOW
Professor Emeritus of Civil and Environmental Engineering
San Diego State University, San Diego,
California
1. INTRODUCTION
There are two characteristic properties in open-channel flow:
(1) velocity; and (2) diffusivity.
Surface flow diffusivity ν
is the first moment of the flow velocity.
The units of diffusivity are (L/T)L, or its equivalent L2/T.
The expression ν = 1 m2/sec,
in relation to a given disturbance,
describes the mathematical certainty
that the disturbance is spreading at the rate controlled by the coefficient of diffusivity
ν.
In fluid mechanics, diffusivity
relates to the process of diffusion;
in hydrology, it relates to flood wave
attenuation, or dissipation.
In hydraulic and hydrologic modeling, diffusivity is described by a differential
equation of second order (Table 1).
These two fluid properties, velocity and diffusivity, characterize the
flow up to
second order.
2. VELOCITIES IN OPEN-CHANNEL FLOW
There are three characteristic velocities in open-channel flow:
(1) the mean velocity of steady flow u;
(2) the relative celerity of kinematic waves v; and (3) the relative
celerity of dynamic waves w.
The celerity of a kinematic wave is: ck = β u, in which
β = exponent of the rating, Q = αAβ,
in which
The celerity of a dynamic wave, which has two components, is: cd = u ±
(gD)1/2, in which
The three velocities identified here encompass both steady (u) and unsteady flow
(v and w), as well as
short waves (dynamic, w), and long waves (kinematic, v).
We note that these are the only flow velocities that are identifiable in the present context.
3. DIFFUSIVITIES IN OPEN-CHANNEL FLOW
Three diffusivities are recognized in open-channel flow: (1) molecular diffusivity;
(2) hydraulic diffusivity; and (3) spectral diffusivity. In fluid mechanics,
the molecular diffusivity νm
is commonly referred to as kinematic viscosity ν,
a measure of the fluid's
internal resistance to flow at the molecular level.
4. STEADY FLOW VELOCITY RATIO: THE FROUDE NUMBER
The Froude number is the ratio of mean flow velocity u
to relative celerity of dynamic waves w: F = u /w (Ponce, 2014b).
It compares the mean flow velocity to the relative celerity of small (short)
surface perturbations;
accordingly, it classifies the flow into three types:
In open-channel hydraulics, the Froude number is useful
in determining the direction of computation
in the analysis of water surface profiles: Upstream for subcritical flow,
and downstream for supercritical flow.
In river mechanics, the Froude number is an indication of the limit between
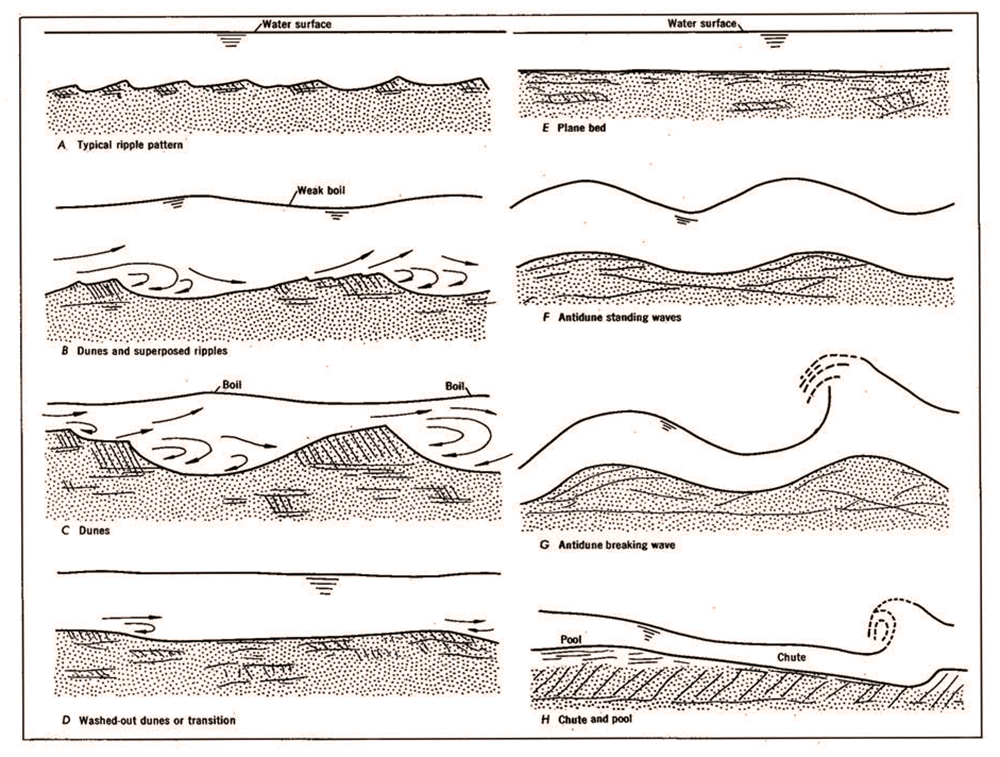
lower regime, F < 0.5,
generally where ripples and dunes predominate in the streambed, and upper regime,
F > 0.5, where plane bed and antidunes prevail
(Simons and Richardson, 1966).
Note the sharp division between subcritical and supercritical flow at F = 1.
The latter constitutes a singular
point, at which the direction of computation
switches instantaneously between upstream and downstream.
The existence of a singularity in the neighborhood of F = 1 may render
the computation unstable; therefore,
caution is recommended in the vicinity of critical flow.
A history of the Froude number, including
Froude's significant contributions to hydraulic engineering,
has been presented by
5. STEADY FLOW DIFFUSIVITY RATIO: THE REYNOLDS NUMBER
The Reynolds number is a ratio of viscosities, or diffusivities.
The conventional Reynolds number,
defined for an arbitrary cross-sectional shape,
in terms of hydraulic radius Ro, is:
R = (uo Ro) / νm
(Ponce, 2014b). For a hydraulically wide channel:
R = (uo do) / νm.
For the purposes of this article,
we define an alternative Reynolds number as an appropriate
ratio of diffusivities,
as follows:
The Reynolds number R classifies the flow as being in one of the following regimes:
6. UNSTEADY FLOW VELOCITY RATIO: THE VEDERNIKOV NUMBER
The Vedernikov number is the ratio of
the relative celerity of a
kinematic wave v to the relative celerity of a dynamic wave w:
V = v /w (Ponce, 2014b).
It characterizes the following states of flow:
Under stable flow,
the relative kinematic wave celerity v is smaller than the relative dynamic wave celerity w
and, therefore, surface waves (perturbations) are able to attenuate (dissipate).
Under
neutrally stable flow, the relative kinematic wave celerity v is equal to the relative dynamic wave celerity w and, therefore, surface waves neither attenuate
nor amplify.
Under unstable flow,
the relative kinematic wave celerity v is greater than the relative dynamic wave celerity w.
Therefore, surface waves are subject to negative attenuation, i.e.,
amplification.
In practice, the condition V > 1 leads to the development
of roll waves, recognized as
a train of waves that travel downstream, typically
in artificial channels of steep slope (Fig. 2).
The flow condition leading to the formation of roll waves may be explained in terms of the
kinematic waves, which transport mass, overcoming the dynamic waves,
which transport energy (Craya, 1952;
Ponce and Choque Guzman, 2019).
The theory of the Vedernikov number (Vedernikov, 1945; 1946),
originally christened by Powell (1948)
and later presented by Chow (1959) in Chapter 8 of his textbook, was clarified by Ponce (1991),
who expressed the Vedernikov number in terms of relative kinematic and dynamic wave celerities.
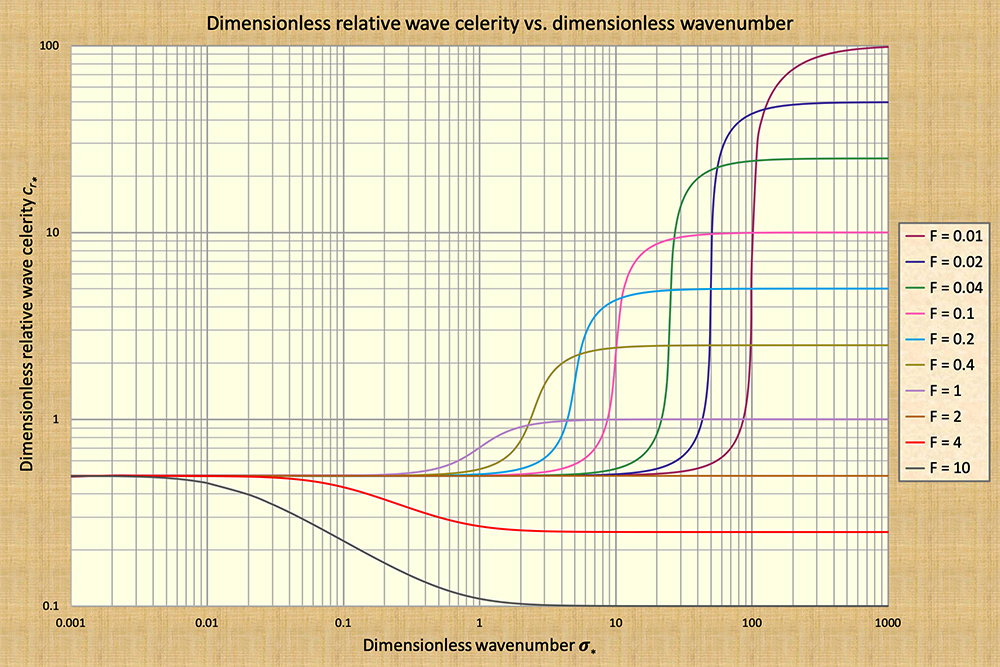
7. UNSTEADY FLOW DIFFUSIVITY RATIO: DIMENSIONLESS WAVENUMBER
The dimensionless wavenumber
of Ponce and Simons (1977) is defined as follows:
σ*
= (2π /L)Lo. Kinematic (extreme left),
Diffusion (left-of-center),
Mixed kinematic-dynamic (right-of-center), and
Dynamic (extreme right).
Kinematic flow:
σ* < 0.001.
Diffusion flow:
0.001 ≤ σ* < 0.17.
Mixed kinematic-dynamic flow:
0.17 ≤ σ* < 1 to 100,
depending on the Froude
number Dynamic flow:
σ* ≥ 10 to 1000, depending on the
Froude number (refer to Fig. 3).
The findings of Ponce and Simons (1977) help to elucidate
the behavior of all possible wave types
in unsteady open-channel flow. The latter include
both "long" waves, ostensibly of a kinematic nature, on the far left
side of Fig. 3, and "short" waves, of a dynamic nature, on the far right.
8. SUMMARY
Four dimensionless numbers in open-channel flow are presented, explained and compared (Table 2).
Two of them are ratios of velocities and
the other two are ratios of diffusivities. All four
numbers are defined in terms of veritable physical quantities, be it either velocities or diffusivities.
Taken together, these numbers complete the description of
the state of flow, for
either steady flow (the first two numbers),
or unsteady flow (the last two).
REFERENCES
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.
Cornish, V. 1907. Progressive waves in rivers. Journal of the Royal Geographical Society, Vol. 29, No. 1, January, 23-31.
Craya, A. 1952. The criterion for the possibility of roll wave formation.
Gravity Waves, National Bureau of Standards Circular No. 521,
National Bureau of Standards, Washington, D.C. 141-151.
Hayami, I. 1951.
On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute,
No. 1, December, Extract.
Ponce, V. M. and D. B. Simons. 1977.
Shallow wave propagation in open channel flow.
Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476.
Ponce, V. M. 1979.
On the classification of open channel flow regimes. Proceedings,
Fourth National Hydrotechnical Conference, Vancouver, British Columbia, Canada.
Ponce, V. M. 1991. New perspective on the Vedernikov number.
Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V. M. 2014.
Fundamentals of Open-channel Hydraulics.
Online text.
Ponce, V. M. and B. Choque Guzman. 2019.
The control of roll waves in channelized rivers.
Online article.
Ponce, V. M. 2023.
When is the diffusion wave applicable?
Online article.
Powell, R. W. 1948.
Vedernikov's criterion for ultra-rapid flow.
Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.
Simons, D. B. and E. V. Richardson. 1966.
Resistance to flow in alluvial channels. Geological Survey Professional Paper 422-J,
U.S. Government Printing Office, Washington, D.C.
Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid.
Doklady Akademii Nauk USSR, 48(4), 239-242.
Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel.
Doklady Akademmi Nauk USSR, 52(3), 207-210.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 240129 |